1. 조합
서로 다른 n개의 물건에서 순서를 생각하지 않고 r개를 택할 때, 이것은 n개에서 r개를 택하는 조합이라 하고, 이 조합의 수를 기호로 nCr와 같이 나타낸다.
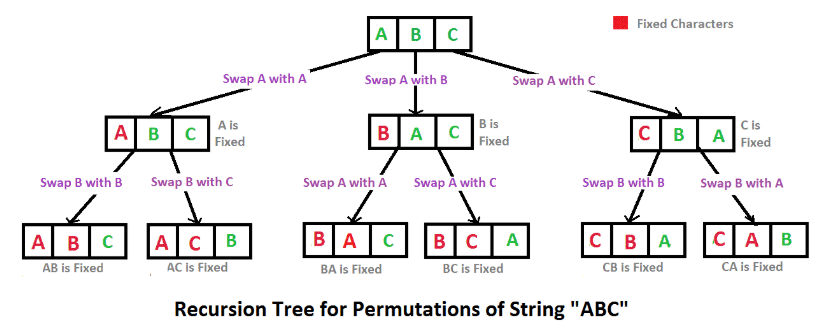
바로 예를 살펴보도록 하자. 4Combination3 = 4C3을 코드로 구현한다면 다음과 같은 인풋과 아웃풋을 가지게 된다.
Input: [1, 2, 3, 4]
Output: [ [1, 2, 3], [1, 2, 4], [1, 3, 4], [2, 3, 4] ]4C3은 4개중에 3개씩 선택할 때 나올 수 있는 모든 조합을 구한다는 말이다. 이 때, 조합의 순서는 상관이 없다. 즉 [1, 2, 3] = [3, 2, 1] 이렇게 순서가 바뀌어도 같은 구성이기 때문에 하나의 조합으로 취급한다는 이야기다.
수도코드
위의 예시를 들어서 수도코드를 작성해보았다.
시작
1을 선택(고정)하고 -> 나머지 [2, 3, 4] 중에서 2개씩 조합을 구한다.
[1, 2, 3] [1, 2, 4] [1, 3, 4]
2를 선택(고정)하고 -> 나머지 [3, 4] 중에서 2개씩 조합을 구한다.
[2, 3, 4]
3을 선택(고정)하고 -> 나머지 [4] 중에서 2개씩 조합을 구한다.
[]
4을 선택(고정)하고 -> 나머지 [] 중에서 2개씩 조합을 구한다.
[]
종료배열의 처음부터 하나씩 선택(고정)하면서 뒤의 나머지의 배열에 대해서 조합을 구해서 붙이면 되는 것이다. 이렇게 나머지에 대해서 일을 위임할 때에는 재귀(Recursion)함수를 사용하는 것이 좋다! 왜냐하면 계속해서 반복 될 일(조합을 구하는 코드)에 대해서 한번만 명시 해 놓고, 들어가는 인자(나를 뺀 나머지)를 바꾸어 주기만 하면 되기 때문이다.
풀이과정
- 재귀 종료 조건: 하나를 선택할 때에는, 모든 배열의 원소를 선택해서 리턴한다.
forEach 문으로, 배열의 모든 원소를 처음부터 끝까지 한 번씩 고정(fixed) 되도록 한다. - 고정(fixed)된 값의 나머지 배열에 대해서 조합을 구하도록 한다. 이 때, 선택하는 개수를 하나 줄인다.
- 조합을 만들어온 결과에 fixed 고정된 값을 앞에 붙여서 리턴할 배열에 spread syntax 로 배열화 한 후에 리턴한다.
- 2C3, 1C2 같이 선택하려는 개수가 많으면 빈 배열이 return 되기 때문에 위의 예에서 3과 4를 선택할 때에는 빈 배열이 돌와아서 최종 결과값에 포함되지 않는다.
로직을 이해하기 위해 하나하나 아이패드에 순서를 손코딩해보았다...😂

코드를 종합해보면
const getCombinations = function (arr, selectNumber) {
const results = [];
if (selectNumber === 1) return arr.map((el) => [el]);
// n개중에서 1개 선택할 때(nC1), 바로 모든 배열의 원소 return
arr.forEach((fixed, index, origin) => {
const rest = origin.slice(index + 1);
// 해당하는 fixed를 제외한 나머지 뒤
const combinations = getCombinations(rest, selectNumber - 1);
// 나머지에 대해서 조합을 구한다.
const attached = combinations.map((el) => [fixed, ...el]);
// 돌아온 조합에 떼 놓은(fixed) 값 붙이기
results.push(...attached);
// 배열 spread syntax 로 모두다 push
});
return results; // 결과 담긴 results return
}2. 순열
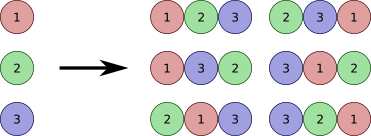
서로 다른 n개의 물건 중에서 r개를 택하여 한 줄로 배열하는 것을 n개의 물건에서 r개 택하는 순열이라 하고, 이 순열의 수를 기호로 nPr와 같이 나타낸다. 조합은 순서에 상관없이 선택한 것이라면, 순열은 순서가 중요하다. 실제로 순열을 구하는 공식도 조합으로부터 도출 가능하다.
Input: [1, 2, 3, 4]
Output: [
[ 1, 2, 3 ], [ 1, 2, 4 ],
[ 1, 3, 2 ], [ 1, 3, 4 ],
[ 1, 4, 2 ], [ 1, 4, 3 ],
[ 2, 1, 3 ], [ 2, 1, 4 ],
[ 2, 3, 1 ], [ 2, 3, 4 ],
[ 2, 4, 1 ], [ 2, 4, 3 ],
[ 3, 1, 2 ], [ 3, 1, 4 ],
[ 3, 2, 1 ], [ 3, 2, 4 ],
[ 3, 4, 1 ], [ 3, 4, 2 ],
[ 4, 1, 2 ], [ 4, 1, 3 ],
[ 4, 2, 1 ], [ 4, 2, 3 ],
[ 4, 3, 1 ], [ 4, 3, 2 ]
]수도코드
먼저, 재귀의 종료 조건은 조합을 구하는 함수와 동일하다. 왜냐하면, 한 개씩 선택한다고 하면 순서가 의미가 없어지기 때문이다.
[1,2,3,4] 에서 3개를 선택해서 순열을 만드는 코드의 내부를 의사코드로 적어보면 다음과 같다.
1, 2, 3, 4를 각각 순서대로 픽스하고 나머지 요소만으로 이루어진 배열에서 (seletNumber-1)만큼을 선택하여 또 순열을 구한다.(재귀)
1(fixed) => permutation([2, 3, 4]) => 2(fixed) => permutation([3, 4]) => ...
2(fixed) => permutation([1, 3, 4]) => 1(fixed) => permutation([3, 4]) => ...
3(fixed) => permutation([1, 2, 4]) ... 위와 동일...
4(fixed) => permutation([1, 2, 3])코드를 종합해보면
const getPermutations = function (arr, selectNumber) {
const results = [];
if (selectNumber === 1) return arr.map((el) => [el]);
// n개중에서 1개 선택할 때(nP1), 바로 모든 배열의 원소 return. 1개선택이므로 순서가 의미없음.
arr.forEach((fixed, index, origin) => {
const rest = [...origin.slice(0, index), ...origin.slice(index+1)]
// 해당하는 fixed를 제외한 나머지 배열
const permutations = getPermutations(rest, selectNumber - 1);
// 나머지에 대해서 순열을 구한다.
const attached = permutations.map((el) => [fixed, ...el]);
// 돌아온 순열에 떼 놓은(fixed) 값 붙이기
results.push(...attached);
// 배열 spread syntax 로 모두다 push
});
return results; // 결과 담긴 results return
}순열과 조합을 JavaScript로 구현해보니... 재귀함수를 왜 쓰는지 이해가 가기 시작했다.
3. 응용문제
정수를 요소로 갖는 배열을 입력받아 3개의 요소를 곱해 나올 수 있는 최대값을 리턴해야 하는 문제에 '조합' 알고리즘을 응용시켜 보았다.
수도코드
배열의 길이가 어떻게 되는지 모르지만, 그 중 3개의 요소를 '순서 상관하지 않고 뽑는 것'이므로, 조합 알고리즘을 선택했다
//일단 3개의 요소를 뽑는 모든 경우의 수를 배열 형태로 나열하고(위 조합 알고리즘 코드 이용)
//그 3개의 요소로 이루어진 2차원 배열에서, 베열 요소를 모두 곱하여(reduce사용)
//2차원 배열 요소에 치환시킨다(반복문)
//그리고 그 배열요소값 중 최대값을 구한다(Math.max.apply이용)코드로 작성해보면
const largestProductOfThree = function (arr) {
//nCr 구하는 함수 선언
//요소마다 누적곱을 해줌
const getCombinations = function (arr, selectNumber) {
const results = [];
if (selectNumber === 1) return arr.map((el) => [el]);
arr.forEach((fixed, index, origin) => {
const rest = origin.slice(index + 1);
const combinations = getCombinations(rest, selectNumber - 1);
const attached = combinations.map((el) => [fixed, ...el]);
results.push(...attached);
});
return results;
}
const resultArr = getCombinations(arr, 3); //조합의 경우를 2차원 배열로 모두 나열
for(let i=0; i<resultArr.length; i++){
resultArr[i] = resultArr[i].reduce((acc, cur)=>acc*cur, 1)
}//요소의 곲으로 치환한 배열로 만들고
return Math.max.apply(null, resultArr) //그 중 최대값 리턴
};구글링하였던 메소드
- forEach문 MDN 자료 참고~
- Math.max.apply 문법


와우 진짜 이해 잘됩니다... 최고!!