JavaScript로 분할정복 알고리즘 구현하기

재귀를 이용해서 보다 빠르게 높은 차수의 거듭제곱 구하기

"a를 n번 곱한것을 구하시오." 라는 것을 보게 되면 일단은 곱셈을 n번 반복하는 방법을 생각하게 되는데, 이 방법은 시간복잡도가 O(n) 이기 때문에 n이 큰 수일 경우에는 굉장히 속도가 느려서 보다 빠른 방법이 필요하다.

거듭제곱에서 다음과 같은 규칙을 찾을 수 있다!

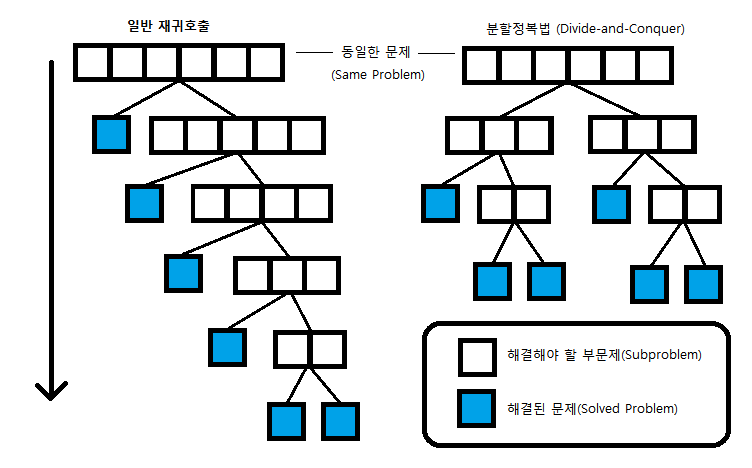
이 규칙을 사용해서 거듭제곱을 구하는 방법을 분할제곱이라 한다.

이 알고리즘의 시간복잡도는 O(log n)이기 때문에 n이 커질 경우에 유용하다.

오늘 토이문제의 주의사항은 아래와 같았다.

• Math.pow, 거듭제곱 연산자 사용은 금지됩니다.
• 시간복잡도 O(logN)을 만족해야 합니다.
• 나머지를 구하는 이유는 계산 결과가 컴퓨터로 나타낼 수 있는 수의 범위를 넘을 수 있기 때문입니다. 하지만 모든 연산이 끝난 뒤에 그 결과를 94,906,249로 나누려고 해서는 안 됩니다. 연산 중간에도 이 범위를 넘을 수 있기 때문에, 연산을 할 때마다 나머지를 구하고 그 결과에 연산을 이어가시기 바랍니다.

수도코드를 작성해보면

//case1. exponent가 0일 때는 1리턴
//case2. exponent가 짝수일 때 exponent를 2로 나눈다
//case3. exponent가 홀수일 때 (exponent-1)를 2로 나눈다.

그리고 주의사항을 참고하여 각 연산을 해줄때마다 94,906,249로 나눠 나머지를 구하는 과정을 추가해주기만 하였다.

코드를 종합해보면

function power(base, exponent) {
  // todo: 여기에 코드를 작성합니다.
  // 중요한 것: 연산을 할 때마다 나머지를 구한다!

  if(exponent === 0){
    return 1;
  }
  if(exponent%2 ===0){
    let byTwo = power(base, exponent/2)%94906249
    return (byTwo * byTwo)%94906249
  }
  else{
    let byTwoPlusOne = power(base, (exponent-1)/2)%94906249
    return (base * ((byTwoPlusOne * byTwoPlusOne)%94906249))%94906249
  }
  
}