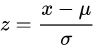Chapter 07. 검증하고 예측하기

강민석·2023년 2월 26일

데이터 분석

목록 보기

7/7

실습 코드 :
7-1: https://colab.research.google.com/drive/1mQ3R_28n2teboJ3u9ON2JarYSlHEh7We?usp=sharing
7-2 : https://colab.research.google.com/drive/1JB55px7AMgm6sOjB9NqZh3BQu14su8QM?usp=sharing

통계적으로 추론하기

모수검정

분석하려는 전체 데이터의 수집이 어려울 때 '샘플(표본)'데이터 수집을 통해 모집단의 특성을 추론하고 검증 할 수 있다.

표준점수(z점수)

데이터가 정규분포를 따른다는 가정 하에 각 값이 평균에서 떨어진 정도를 표현.

x: 정상화되는 원수치.

σ: 모집단에서의 표준편차.

μ: 모집단에서의 평균.

파이썬으로 표준 점수 구하기

numpy를 활용(원소 7)

import numpy as np

x = [0, 3, 5, 7, 10]

s = np.std(x)
m = np.mean(x)
z = (7 - m) / s

print(z)

> 0.5872202195147035

scipy를 활용

from scipy import stats

stats.zscore(x)
> array([-1.46805055, -0.58722022,  0.        ,  0.58722022,  1.46805055])

누적분포

특정 z점수 내에 있는 샘플의 비율을 표현

scipy.stats.norm은 표준정규분포를 반환한다.
cdf()메서드는 누적분포를 계산한다.
표준정규분포의 z점수 0까지는 정확히 절반이다.

stats.norm.cdf(0)
> 0.5

z점수 1 이내의 비율

stats.norm.cdf(1.0) - stats.norm.cdf(-1.0)
> 0.6826894921370859

ppf()메서드는 특정 비율에 해당하는 z점수 반환

stats.norm.ppf(0.9)
> 1.2815515655446004

중심극한정리

무작위로 샘플을 뽑아 만든 표본들의 평균은 정규분포에 가깝다

sample() (샘플링)

np.random.seed(42)
sample_means = []
for _ in range(1000):
    m = ns_book7.대출건수.sample(30).mean()
    sample_means.append(m)

plt.hist(sample_means, bins=30)

대출건수 분포 -> 샘플링한 평균의 분포

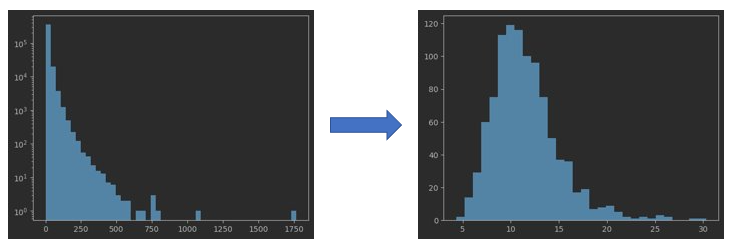
샘플링 크기와 정확도

중심극한정리를 따르려면 샘플 크기는 30이상인 것이 좋다.

모집단의 평균 : 11.593438968070707

샘플 크기 30의 표본평균의 평균 : 11.539900000000001
샘플 크기 20의 표본평균의 평균 : 11.39945 (가장 불일치)
샘플 크기 40의 표본평균의 평균 : 11.5613 (가장 유사)

표준오차

표본평균의 표준편차는 모집단의 표준편차를 표본 크기의 제곱근으로 나눈것에 가깝다.

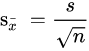
표본평균의 표준편차 (표준오차)

np.std(sample_means)
> 3.0355987564235165

모집단의 표준편차 / 샘플개수의 제곱근

np.std(ns_book7.대출건수) /np.sqrt(40)
3.048338251806833

신뢰구간

표본의 속성이 속할 것이라 믿는 모집단의 속성 범위

평균의 신뢰구간

표본의 평균만 알고 있을 때

표본 : 파이썬 도서들과 그 대출건수,
-> 수량 : 251개, 평균 : 14.71, 95%구간

모집단의 평균 = 표본평균 - z * (모집단 표준편차 / 표본갯수의 제곱근)

중심극한정리를 활용해 표본의 표준편차는 모집단의 표준편차와 비슷하다고 가정

python_std = np.std(python_books.대출건수)
python_se = python_std / np.sqrt(len(python_books))
python_se
> 0.8041612072427442(평균의 표준편차와 유사)

95% 구간의 z점수 구하기

stats.norm.ppf(0.975)
> 1.959963984540054
stats.norm.ppf(0.025)
> -1.9599639845400545

공식 다시보기
모집단의 평균 = 14.75 - z(+-1.959963984540054) * 0.8041612072427442
계산 결과

print(python_mean-1.96*python_se, python_mean+1.96*python_se)
> 13.172848017867965 16.325159950259522

해석
'95% 신뢰구간에서 모집단 평균이 13.2에서 16.3 사이에 놓여있다.`

가설검정

표본에 대한 정보를 사용해 모집단의 파라미터에 대한 가정을 검정

영가설(귀무가설) : 표본 사이에 통계적으로 의미가 없다

대립가설 : 표본사이에 통계적인 차이가 있다

유의수준 : 두 가설 중의 채택 기준이되는 z점수. 주로 p-값(정규분포의 양쪽 꼬리면적의 합이 5%)

z점수로 가설 검증하기

표본1: 파이썬 도서들과 그 대출건수
-> 수량 : 251개, 평균 : 14.71, 95%구간
표본2 : C++ 도서들과 그 대출건수
-> 수량 : 89개, 평균 : 11.59, 95%구간

가설검정(z-score) 공식

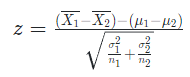
cplus_se = np.std(cplus_books.대출건수) / np.sqrt(len(cplus_books))
cplus_se
> 0.9748405650607009 (표준오차)

z = (14.75 - 11.59) / (0.8^2 + 0.97^2).제곱근

(python_mean - cplus_mean) / np.sqrt(python_se**2 + cplus_se**2)
> 2.495408195140708 (z점수)

stats.norm.cdf(2.50)
> 0.9937903346742238

-> 95%지점인 유의수준준을 벗어나므로 대립가설 지지

t-검정 scipy - ttest_ind()

t분포 : 정규분포보다 중앙이 낮고 꼬리가 두꺼운 분포. 표본 크기가 30보다 낮을때 유용

t, pvalue = stats.ttest_ind(python_books.대출건수, cplus_books.대출건수)
print(t, pvalue)
> 2.1390005694958574 0.03315179520224784(p값)

-> p- 값이 0.05보다 작으므로 대립가설 지지

순열검정

모집단의 분포가 정규분포를 따르지 않거나 모집단의 분포를 알 수 없을 때 사용

진행 방법

두 표본의 평균의 차이를 계산
두 표본을 섞고 원래 표본의 같은 크기로 무작위로 배분
다시 평균의 차이를 계산
이를 여러번 반복하여 원래 표본 평균 차이와 무작위로 나눈 그룹의 평균의 차이를 비교

파이썬 함수로 구현

def statistic(x, y):
    return np.mean(x) - np.mean(y)
    
def permutation_test(x, y):
    obs_diff = statistic(x, y)

    all = np.append(x, y)
    diffs = []
    np.random.seed(42)

    for _ in range(1000):
        idx = np.random.permutation(len(all))

        x_ = all[idx[:len(x)]]
        y_ = all[idx[len(x):]]
        diffs.append(statistic(x_, y_))

    less_pvalue = np.sum(diffs < obs_diff) / 1000
    greater_pvlaue = np.sum(diffs > obs_diff) /1000

    return obs_diff, np.minimum(less_pvalue, greater_pvlaue) * 2

permutation_test(python_books.대출건수, cplus_books.대출건수)
> (3.1534983660862164, 0.022(p-값))

scipy - permutation_test()

res = stats.permutation_test((python_books.대출건수, cplus_books.대출건수), statistic, random_state=42)
print(res.statistic, res.pvalue)
> 3.1534983660862164 0.0258

머신러닝으로 예측하기

머신러닝 용어

모델 : 특정 알고리즘을 대변하거나 머신러닝 소프트웨어 등을 구체적으로 나타냄.

지도 학습 : 데이터의 각 샘플에 대한 정답(타깃)을 알고 있는 경우 사용. 입력과 정답을 통해 학습 후 정답을 모르는 입력에 반영하여 사용.

비지도 학습 : 입력은 있지만 타깃이 없는 경우. 타깃을 도출하기 매우 어렵거나 비용이 높음.

모델 훈련하기

모델 훈련 후 새로운 데이터를 사용해 모델을 평가함.
훈련 세트 : 훈련에 사용되는 입력, 타깃.
테스트 세튼 : 테스트에 사용되는 입력, 타깃. 보통 훈련 세트의 20~25% 크기를 사용함.

훈련 세트와 테스트 세트 나누기 scikit-learn - train_test_split()

데이터를 무작위로 섞은 후 75% / 25% 비율의 세트로 반환.

test.size = 분할 비율 조정

from sklearn.model_selection import train_test_split

train_set, test_set = train_test_split(ns_book7, random_state=42)

데이터의 '도서권수'와 '대출건수'를 2차원 배열과 1차원 배열로 변환

사이킷 런의 입력으로 2차원 배열과 1차열 배열을 받기 때문.

X_train = train_set[['도서권수']]
y_train = train_set['대출건수']

print(X_train.shape, y_train.shape)

선형 회귀 모델 훈련하기

LinearRegression class아래의 fit()메서드를 호출

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(X_train, y_train)

훈련된 모델 평가하기

결정계수 score()

모델의 점수를 평가한 것으로서 정확할수록 1에 가까워짐

앞서 제작한 테스트 세트를 이용해 훈련한 모델을 평가한다.

X_test = test_set[['도서권수']]
y_test = test_set['대출건수']

lr.score(X_test, y_test)
> 0.10025676249337057 (결정계수)

선형 회귀 모델

https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%ED%9A%8C%EA%B7%80

로지스틱 회귀

연속적인 실수 출력값을 1 또는 0으로 변환

회귀 : 타깃이 실수인 문제
범주 : 타깃이 어떤 종류의 카테고리(범주, class)인 문제. ex) 개<>고양이<>사람

이진 분류 : 카테고리가 두 개인 경우(음성 클래스(0) <> 양성 클래스(1))
다중 분류 : 카테고리가 세 개 이상인 경우

로지스틱 회귀 모델 훈련하기

대출건수가 평균보다 높은 것을 양성 클래스로 설정

borrow_mean = ns_book7.대출건수.mean()
y_train_c = y_train > borrow_mean
y_test_c = y_test > borrow_mean

양성, 음성 클래스 분포 확인하기

y_test_c.value_counts()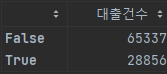

LogisticRegression()으로 훈련 및 평가

from sklearn.linear_model import LogisticRegression

logr = LogisticRegression()
logr.fit(X_train, y_train_c)
logr.score(X_test, y_test_c)
> 0.7106154385145393

Dummy 모델 적용.

가장 많은 클래스로 무조건 예측을 수행함.

DummyRegressor : 무조건 타깃의 평균을 예측함.
DummyClassifier : 가장 많은 클래스로 예측함.

from sklearn.dummy import DummyClassifier

dc = DummyClassifier()
dc.fit(X_train, y_train_c)
dc.score(X_train, y_train_c)
> 0.6926182951903375

결과

로지스틱 회귀의 정확도가 70% 정도이지만, 음성 클래스의 양도 70%정도이고 더미테스트의 결과도 69%를 기록하므로 의미없는 결과 도출됨.

소감

지난 몇 주간 그래프 그리기 등의 가벼운 내용을 접하다가 통계나 머신러닝 기법의 새로운 용어들을 마주치니 학습에 시간이 많이 걸렸다. 흥미로웠던 것은 파이썬의 패키지들에서 머신러닝 수행부터 평가까지 많은 기능을 제공해주고 있어 활용만 제대로 하면 초보적인 수준의 머신러닝은 누구나 가능한 점이었다. 때문에 머신러닝에서 가장 중요한 것은 올바른 모델과 데이터를 선정하는 것임을 다시한번 느낄 수 있었다.

강민석

새내기 개발자입니다.

이전 포스트