[Math] 10진수 2진법 변환

2진수 > 10진수 진법 변환

공식 : 변환하고자 하는 수 x n^(자리수-1)

1) 2진수는 0과 1로만 표현하므로, 0은 곱셈 해봤자 0, 2진수의 자리가 1인 수만 곱셈
2) 여기서 n은 진법을 뜻한다. 2진법이므로 2를 곱셈
3) 자리수-1은, 2진수의 자리를 뜻한다. 첫 번째 자리라면 1-1=0, 2^0승이 된다. (1)
4) 예를 들면, 2진수 10이 있다면 첫 번째 자리는 0이고 두 번째 자리는 1이다.
0은 곱셈하지 않으므로, 두 번째 자리 1은 ( 1 x 2^(2-1) == 1 x 2^1 ) 즉 2가 된다.
2진수 10은, 10진수로 2라는 뜻입니다.

1011(2)를 10진수로 변환 과정 (1) ↓

1 번쨰 자리 : 1 x 2^0 = 1 x 1 = 1
2 번째 자리 : 1 x 2^1 = 1 x 2 = 2
3 번째 자리 : 0 x 2^2 = 0 x 4 = 0
4 번째 자리 : 1 x 2^3 = 1 x 8 = 8

결과로 나온 모든 자리의 수를 더하면 10진수가 나옵니다. ( 1+2+0+8 = 11(10진수) )

❓ 1 번째 자리에서 1x1 이 된 이유는?

2^(자리수-1)승 이기 때문입니다. 첫 번째 자리에서 2^은 2^(1-1) = 2^0승이 됩니다.
2의 0승(2^0)은 1이므로, 1x1이 된 것입니다.

101111(2)를 10진수로 변환 과정 (2)↓

(1)번 변환 과정이 어렵다고 느껴지면 아래처럼 풀어서 변환 하세요.
2진수의 자리 수 만큼 2^0승으로 표현하고, 2진수에서 1인 수만 덧셈합니다.

1  0  1  1  1  1
-----------------	> 2진수가 0인 수는 덧셈에서 제외 > 32+8+4+2+1 = 47(10)진수가 된다.
32 16 8  4  2  1 

32 : 2^5
16 : 2^4
8 : 2^3
4 : 2^2
2 : 2^1
1 : 2^0

10진수에서 2진수로 변환 과정

단순하게 10진수를 2로 나눠서, 몫과 나머지를 배열하면 됩니다.
47(10) 진수를 2진수로 나눈다고 가정 시, 47을 마지막 몫이 1이 될 때 까지 나누고
마지막 몫과 나머지들을 차례대로 배열하면 2진수가 됩니다.

10진수 소수부를 2진수 변환 과정

정수는 위처럼 간단하게 계산할 수 있는데, 정수가 아닌 소수부를 2진수로 변환해야 하는
경우도 있습니다. 소수부를 가진 정수를 2진수로 변환하는 과정을 살펴보겠습니다.

47.75 라는 소수부를 2진수로 변환

1) 먼저 정수부와 소수부를 나누어서 진법 변환 해야한다. (47) (0.75)
2) 정수부분 47을 2진수로 변환하면 101111(2)가 됩니다.
3) 소수부분은 정수와 반대로 0.75라는 수를 2로 계속 곱셈합니다. 소수부분이 0이 될 때까지
곱셈과정중에 정수부분만 따로 가져가서 101111(2) 뒤에 소수부로 붙여줍니다.

4) 소수부 연산 과정
0.75 x 2 =1.5 여기서 정수 1은 가져가고, 소수부가 0이 아니기에 다시 연산 수행
101111.1(2) (1을 47가 2진수로된 부분에 소수부로 붙여줍니다)

1을 가져갔기에 .5는 0.5가 됩니다.
0.5 x 2 = 1.0 ( 정수 1을 가져가고, 소수부가 0이 되었기에 연산을 중지합니다 )
101111.11(2)

즉, 47.75는 2진수로 표현하면 101111.11(2)가 됩니다.

2진수의 값이 10진수가 맞는지 확인

위에서 2진수로 표현한 101111.11(2)가 10진수가 맞는지 확인하려면 연산을 수행해보면 됩니다.
이 또한 정수와 소수부분을 나눠서 연산해야 합니다.

✅ 정수부 101111

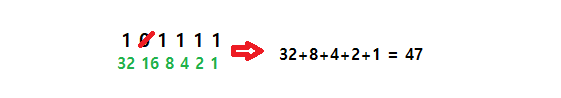
✅ 소수부 .11

정확히 맞아 떨어집니다.

⚠️ 소수 부분이 계속해서 나눠진다면 어떻게 해야 하나요?

10같은 경우도 3으로 나눠보면, 0.3333 무한 소수가 됩니다. 이럴 경우는 적당한 수에서
반올림하면 됩니다. 0.3333~~ 반올림 해버리면 나머지 수는 버리므로 0.3
상황에 따라 다르므로, 무한 소수는 반올림해서 기존 수의 근삿값으로 만들 수 있다
정도로만 생각합시다.