이번 글의 내용과 이미지는 Inflearn에 있는 아래 강의를 참고하여 작성하였습니다.
블로그 내용에 관해 수정할 사항이나 논의할 사항이 있다면 언제든 연락 부탁드립니다.
LinkedIn : devyulbae
Email : devyulbae@gmail.com
목차
1. 왜 Determinant가 중요한가?
2. Determinant란 무엇인가?
2-1. Determinant의 특성
2-2. Det A = 0의 의미
3. Determinant의 응용
4. 결론
1. 왜 ‘Determinant’가 중요한가?
Determinant(행렬식)은 선형대수학을 배울 때 반드시 배우며 중요하게 여기는 부분입니다. 그것은 바로, Determinant가 공간의 변화를 이해하는 열쇠의 역할이기 때문입니다. 우리는 행렬을 이용하여 벡터를 회전시키거나 확대시키는 등 다른 벡터로 변환합니다. 이 때, Determinant는 많은 정보를 알려줍니다. 행렬의 Column 벡터가 서로 독립적인지, 변환 후의 벡터가 차원축소되었는지와 같은 정보를 제공해주죠. 따라서 데이터 분석과 머신러닝에서는 Determinant를 통해 고차원 데이터가 어디에 치우쳐져 있는지, 얼마나 퍼져 있는지 등의 정보를 파악합니다.
오늘은 이 Determinant에 대해서 이해하고, 어떻게 적용하는 지에 대해서 다루어 보겠습니다.
2. Determinant란 무엇인가?
Determinant는 어떤 정사각행렬 A에 대해 정의된 스칼라 값입니다. 기하학적으로는 행렬식이 차지하는 공간의 크기를 나타냅니다. 즉, det A는 2차원에서는 평행사변형의 면적, 3차원에서는 평행육면체의 부피입니다. 기호로 표기할 때에는 |A| 또는 det(A)를 사용하며, 2x2 행렬인지 혹은 3x3 이상의 행렬인지 나누어서 다음과 같이 계산됩니다.
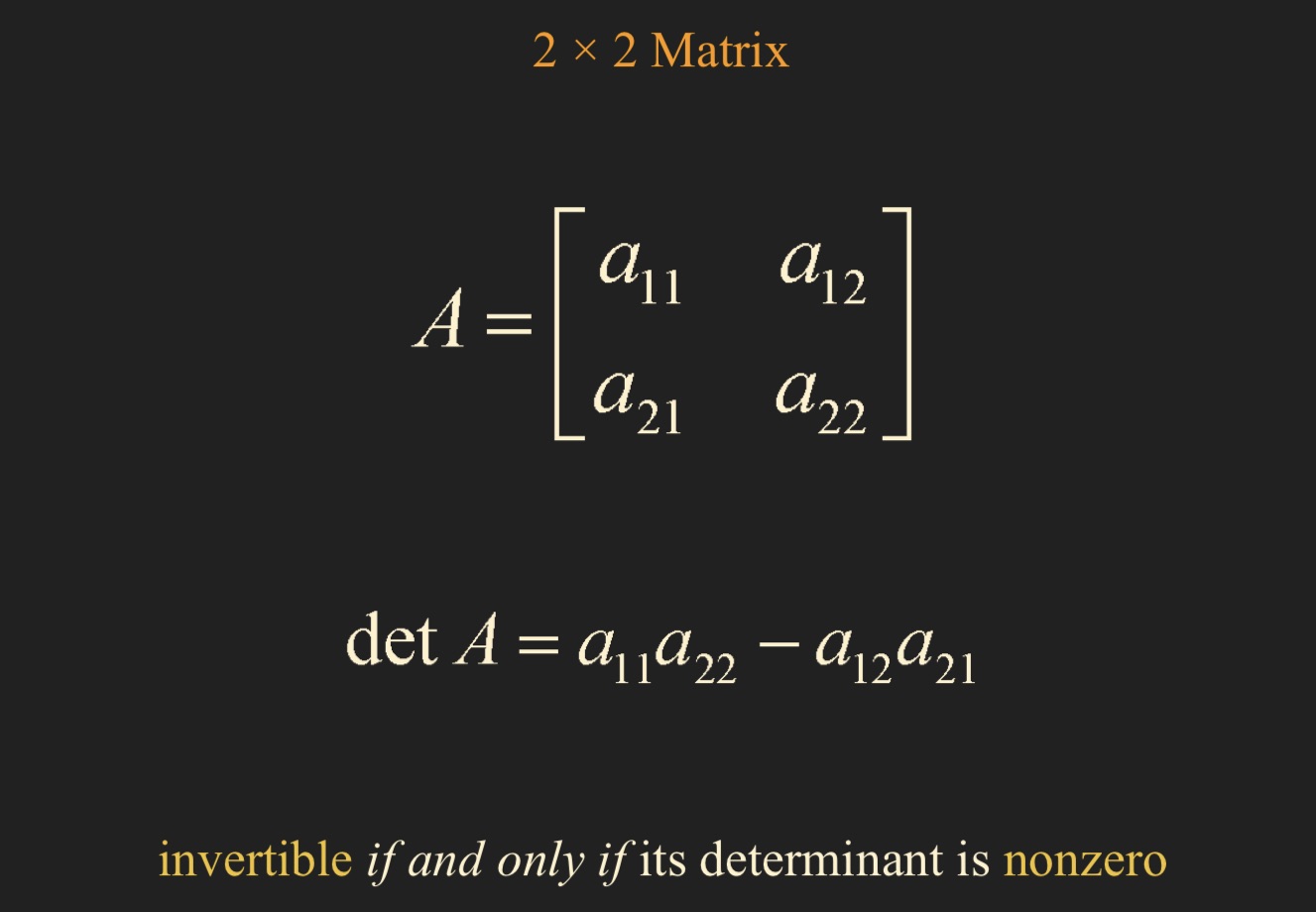
2x2 행렬 : det(A) = ad - bc - 소행렬식
3x3 이상의 행렬 : 소행렬식을 이용한 재귀적 계산

즉, 3x3 이상의 행렬에서는 행렬 내에서 2x2 행렬의 소행렬식을 계산하여 축소하고, 이 과정을 반복해서 마지막 2x2 행렬의 계산을 통해 det A의 스칼라 값이 도출됩니다. 즉, 이 계산의 시간 복잡도는 O(n!)이며, 행렬의 차수가 늘어날수록 det A를 구하기 위한 계산량이 기하급수적으로 증가합니다. 따라서 고차원 행렬에서는 Determinant 대신 특이값 분해(Singular Value Decomposition), 고윳값 분석 등의 방법을 사용합니다.
2-1. Determinant의 특성
Determinant는 여러 대수적인 성질을 가지고 있으며, 이를 통해 계산을 줄일 수 있습니다.
1. det와 det의 곱
이는 determinant의 계산이 곱셈적으로 이루어진다는 것을 의미합니다.2. 전치 연산
전치 연산은 행렬식 값에 영향을 주지 않습니다.3. 스칼라 곱
n x n 행렬 A와 스칼라 c에 대하여,
$A$의 하나의 행에 스칼라 $c$를 곱하면 행렬식은 $c det(A)$가 됩니다.
따라서 $det(cA)$는 $A$의 모든 행에 $c$가 곱해지기 때문에 $c^n$가 되어서 나오게 됩니다.4. 선형 독립성의 파악
특정 행 또는 열이 다른 행 또는 열의 선형 조합인 경우
특정 행이 다른 행의 선형 조합이라는 것은 아래와 같은 의미입니다.
- $A$가 선형 독립이 아닌 선형 종속적이다.
- $A$의 rank가 n보다 작다.
- free variable(자유 변수)를 가진다.
- 이 행렬로 계산된 벡터의 차원을 축소시킨다.4. 차원 결정
det(A) 값에 따라서
det(A) > 0 : 변환 후 공간의 방향이 유지됩니다.
det(A) < 0 : 변환 후 공간의 방향이 반전됩니다.
(예: 좌표계가 뒤집힘)
det(A) = 0 : 변환 후 공간이 붕괴되어 차원이 축소됩니다.
2-2. Det A = 0의 의미
Determinant가 0일 때, 이는 단순히 숫자 하나가 아니라 행렬 변환의 중요한 특성을 나타냅니다. det(A) = 0은 변환 후 공간이 붕괴되었음을 의미하며, 이는 선형 독립성, 영공간, 그리고 역행렬 존재 여부와 밀접하게 연결됩니다.
선형 독립성과 영공간
det(A) = 0이라는 것은 행렬 A의 열 벡터 또는 행 벡터가 선형적으로 독립하지 않다는 뜻입니다. 쉽게 말해, 한 벡터가 다른 벡터들의 조합으로 표현될 수 있다는 것이죠. 이로 인해 행렬 A는 전체 공간을 완전히 “채우지” 못하고, 일부 차원이 붕괴됩니다. 예를 들어, 3차원 공간에서 det(A) = 0인 경우, 변환된 공간이 평면이나 직선으로 축소됩니다. 이는 영공간(null space)이 존재한다는 것을 의미하며, 특정 벡터들이 변환 후 0으로 사상된다는 것을 보여줍니다.
행렬 변환의 특성
Determinant가 0인 경우, 행렬 변환은 가역적(invertible)이지 않습니다. 즉, 변환된 결과에서 원래의 입력값을 복원할 수 없다는 뜻입니다. 이는 선형 시스템에서 매우 중요한 의미를 가지며, 예를 들어 Ax = b라는 선형 방정식에서 det(A) = 0이면 유일한 해를 보장할 수 없습니다. 해가 없거나 무한히 많은 해가 존재하게 됩니다.
역행렬 존재 여부
Determinant는 역행렬의 존재 여부를 판단하는 데 핵심적인 역할을 합니다. 이면 행렬 A는 가역적(invertible)이며, 역행렬 이 존재합니다. 하지만 이라면 역행렬이 존재하지 않으며, 이는 A가 “특이 행렬(singular matrix)“임을 나타냅니다.
즉, not invertible = singular matrix = is 이다.
3. Determinant의 응용
Determinant는 단순히 이론적인 개념에 그치지 않고 다양한 실무 분야에서 중요한 역할을 합니다. 특히 데이터 과학과 머신러닝에서는 차원 축소와 특징 추출 등 핵심적인 작업에 활용됩니다.
머신러닝에서의 활용 (PCA, 선형 회귀)
Principal Component Analysis(PCA)는 고차원 데이터를 저차원으로 축소하는 데 사용되는 기법으로, 데이터가 분산되어 있는 방향(주성분)을 찾는 것이 핵심입니다. 이 과정에서 covariance matrix(공분산 행렬)의 determinant는 데이터가 얼마나 퍼져 있는지를 나타내며, 이를 통해 주요 성분을 선택합니다.
또한 선형 회귀에서도 determinant는 독립 변수들의 선형 독립성을 확인하는 데 사용됩니다. Linear Regression처럼 가중치의 계산에 역행렬이 필요할 경우, determinant가 0인지 확인하여 역행렬이 존재하는지 확인해볼 수 있죠.
또한, determinant가 0에 가까울수록 multicollinearity(다중공선성)이 존재할 확률이 높으므로 정규화 기법을 적용할 근거가 될 수 있습니다.
차원 축소와 특징 추출
Determinant는 차원 축소에서도 중요한 역할을 합니다.
예를 들어, 특정 행렬 변환이 데이터의 분산(variance)을 얼마나 잘 유지하는지 평가할 때 determinant를 사용할 수 있습니다. 특히 Singular Value Decomposition(SVD)과 같은 기법에서는 determinant는 아니지만 유사한 개념이 데이터 압축과 복원을 위한 기준으로 활용됩니다.
가우시안 분포
다변량 가우시안 분포에서는 공분산 행렬의 Determinant가 확률밀도함수(PDF)에 직접적으로 사용됩니다.
확률밀도함수의 정의가 다음과 같을 때, 여기서 가 공분산 행렬의 Determinant입니다. 이 계산식은 우리가 흔히 쓰는 이상치 탐지나, 흔치는 않지만 가우시안 모델, 베이지안 네트워크 등에서도 사용됩니다.
4. 결론
Determinant는 ML분야에 깊게 파고들수록 기본기로서 활용되는 개념입니다. 이 글을 통해 Determinant를 알게 되셨다면, 끄덕이고 넘어가는 것이 아니라 직접 2x2, 3x3, 4x4 Matrix의 Determinant를 계산해보면서 익히시고 실제로 determinant가 사용되는 이상치 탐지, 다중공선성 판별, PCA 등에서도 계산 과정을 뜯어보며 이해해보시면 좋을 거 같습니다.
