최단 경로 알고리즘
말 그대로 가장 짧은 경로 를 찾는 알고리즘이다.
Dijkstra
✔️ 다익스트라 알고리즘은 하나의 출발점을 기준으로 다른 모든 정점까지의 최단 거리를 구할 때를 활용할 수 있는 알고리즘
✔️ 다익스트라는 매번 '가장 비용이 적은 노드'를 선택해서 임의의 과정을 반복하는데, 이 때문에 기본적으로 그리디 알고리즘으로 분류된다.
✅ 프로세스
다익스트라 알로리즘은 최단 거리를 찾기 위해 시작 정점에서부터 인접한 정점들을 하나씩 방문하며 해당 정점까지의 거리를 갱신해 나간다.
인접한 정점들을 하나씩 방문한다는 점에서 BFS와 유사하지만, 동시에 해당 정점들까지의 거리를 갱신해나가야 하기 때문에 몇 가지 자료구조가 더 필요하다.
-
시작 정점부터 다른 정점까지의 거리를 기록하는 리스트
처음에는 무한대로 초기화하고, 더 작은 경로를 찾을 때마다 거리 값을 갱신한다. -
가장 가까운 정점을 꺼내올 수 있는 우선순위 큐
BFS에서는 다음에 방문할 정점들을 큐에 넣었지만, 다익스트라에서는 지금까지 발견된 가장 가까운 거리의 정점에 대해서 먼저 계산할 수 있도록 우선순위 큐에 인접 정점들을 저장한다. 가장 가까운 정점부터 큐에서 꺼내며 미리 거리를 갱신해 놓으면, 그보다 더 먼 거리의 경로에 대해서는 더 이상 고려할 필요가 없어진다.
✔️ 그림으로 프로세스를 알아보자
1. 시작 노드를 설정하고 우선순위 큐에 넣는다
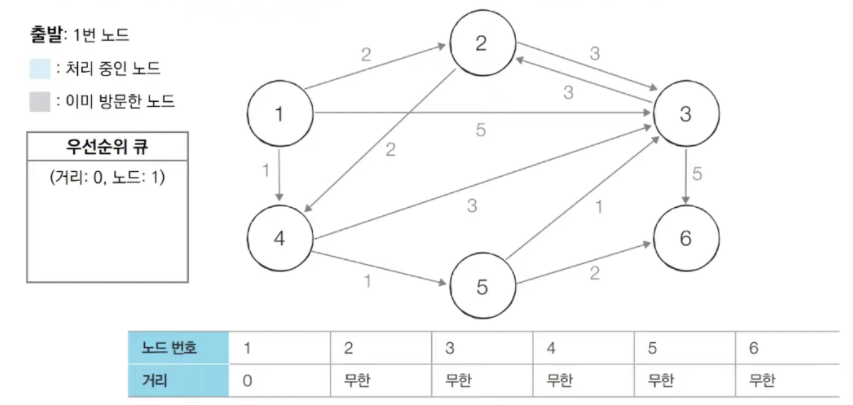
-
우선순위 큐에서 첫번째 원소를 꺼낸다. 1번 노드 방문 안했었으니까 방문했다 하고 처리해줌
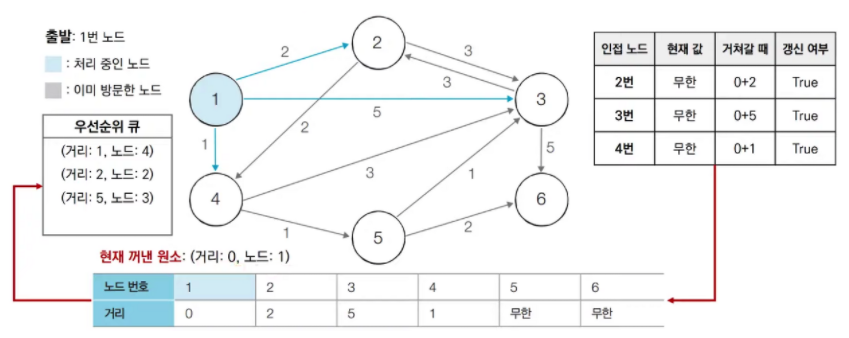
-
우선순위 큐에서 4번 노드를 pop 한다. => 거리가 제일 짧
4번 노드는 방문한 적이 없으므로 4번 노드를 처리
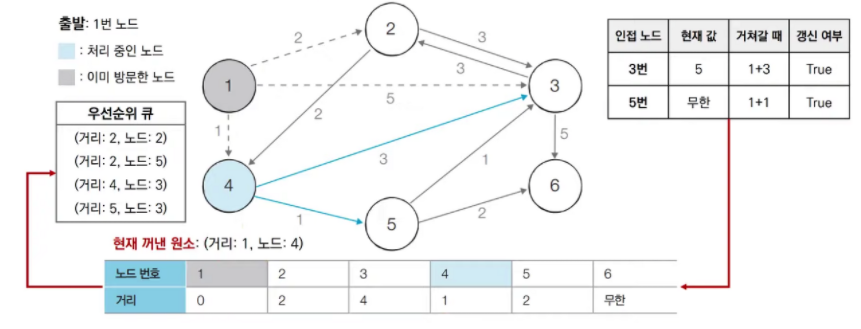
-
우선순위 큐에서 2번 노드를 pop 한다. 2번 노드는 방문한 적이 없으므로 2번 노드를 처리
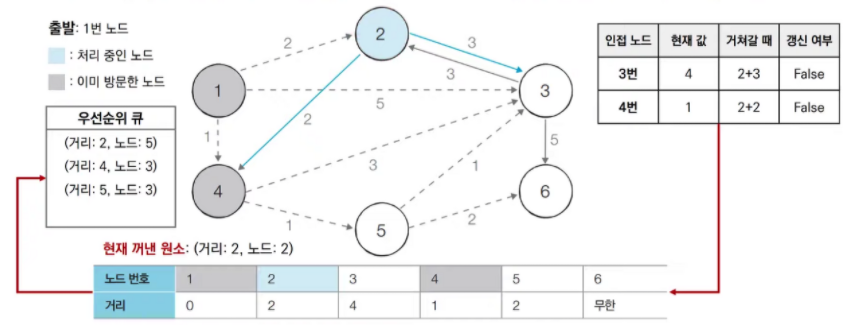
-
우선순위 큐에서 5번 노드를 pop 한다. 5번 노드는 방문한 적이 없으므로 5번 노드를 처리
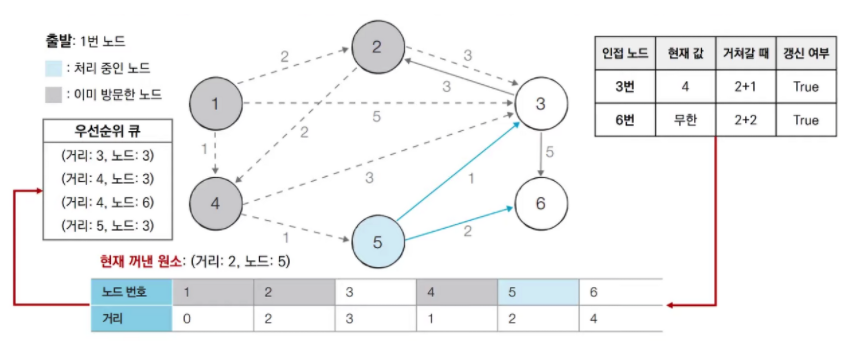
-
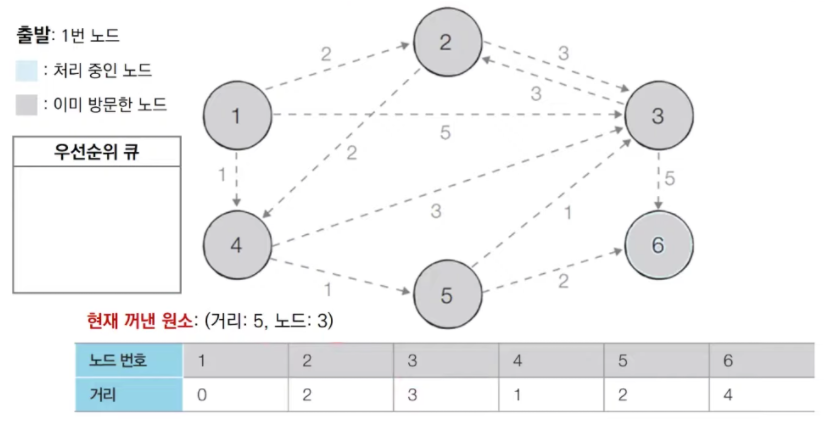
우선순위 큐에서 3번 노드를 pop 한다. 3번 노드는 방문한 적이 없으므로 3번 노드를 처리
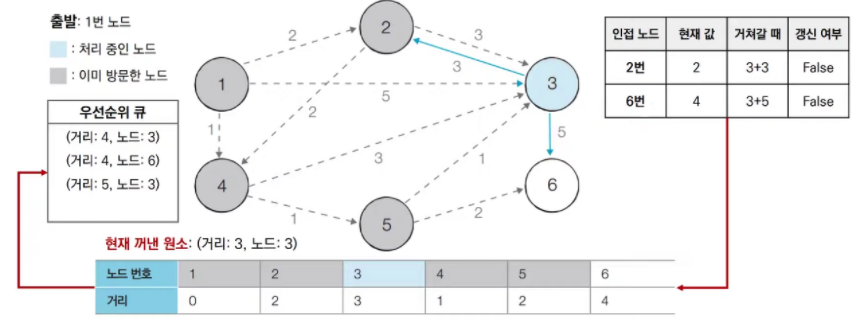
-
우선순위 큐에서 3번 노드를 pop 한다. 하지만 3번 노드는 전 단계에서 방문했으므로 무시하고 건너뛴다.
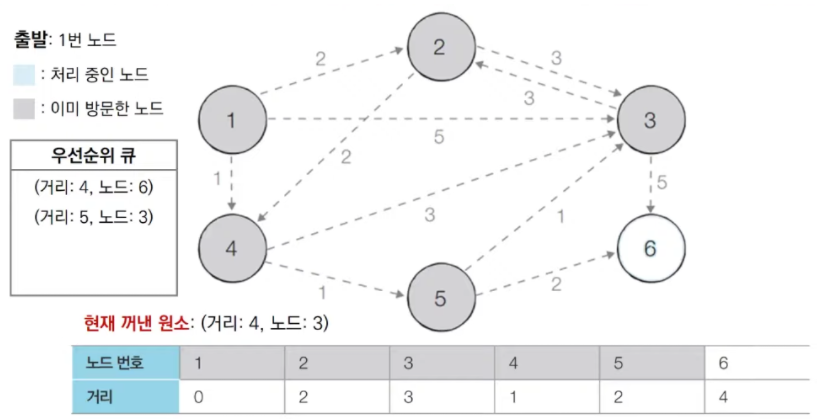
-
계속 위와 동일하게 이미 방문하여 처리가 끝난 노드이면 무시하고 건너뛰고, 방문한 적이 없다면 해당 노드를 처리한다.
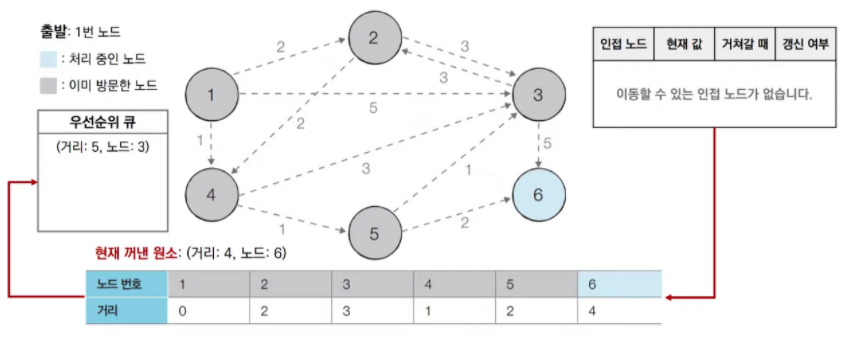
-
그래서 결과는 1 => 4 => 2 => 5 => 3 => 6
✅ Performance : O(ElogE)
다익스트라 알고리즘은 크게 각 정점마다 인접한 간선들을 탐색하는 과정 과 우선순위 큐에 거리, 정점 정보를 넣고 빼는 과정으로 나뉜다.
-
각 정점마다 인접한 간선들을 탐색하는 과정
각 노드는 최대 한 번씩 방문하기 때문에 그래프의 모든 간선은 최대 한 번씩 검사한다. 따라서 이 과정의 시간 복잡도는 O(E)이다. -
우선순위 큐에 [거리, 정점] 정보를 넣고 빼는 과정
최악의 경우는 모든 간선을 검사할 때 마다 거리 값 리스트가 갱신되고, 우선순위 큐에 정보가 저장되는 경우이다. E개의 간선을 검사할 때 마다 우선순위 큐를 유지해야 하므로 이 과정의 시간 복잡도는 O(ElogE)이다.
위 두 과정을 거칠 경우 다익스트라 알고리즘의 총 시간 복잡도는 O(E) + O(ElogE) = O(ElogE) 가 된다.
Floyd-Warshall
다익스트라, 벨만-포드 알고리즘으로 주어진 하나의 정점으로부터 다른 모든 정점들까지의 최단 경로를 구할 수 있었다면, 플로이드-워셜 알고리즘을 활용하면 모든 정점들간의 최단 경로를 구할 수 있다
✔️ 간단하게 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우
✔️ 플로이드-워셜 알고리즘은 경유하는 정점에 초점을 두고, 그 정점을 거쳐가는 경로가 기존 경로보다 더 효율적인지를 판단한다.
✔️ 즉, 경유하는 정점의 입장에서 어떤 정점 u가 다른 정점 v로 갈 때 자신을 거쳐서 가는 것이 기존의 경로보다 더 효율적이라면 기존의 경로를 갱신해주는 작업을 반복하는 것이다.
🚀 다익스트라 vs 플로이드-워셜
📌 다익스트라
- 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다.
이후 해당 노드를 거쳐가는 경로를 확인하며 최단 거리 테이블을 갱신하는 방식으로 동작 - 다익스트라는 한 지점에서 다른 지점까지의 최단 거리이기 때문에 1차원 리스트에 저장
- 다익스트라는 그리디 알고리즘임
📌 플로이드-워셜
- 단계마다 '거쳐 가는 노드'를 기준으로 알고리즘을 수행한다. 하지만, 매 단계마다 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다!
- 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장
- 플로이드 워셜 알고리즘은 DP 알고리즘에 속한다. 왜냐하면 만약 노드의 개수가 N개라고 할 때, N번 만큼의 단계를 반복하며
점화식에 맞게2차원 리스트를 갱신하기 때문에 DP라고 볼 수 있다.
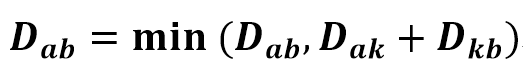
✅프로세스
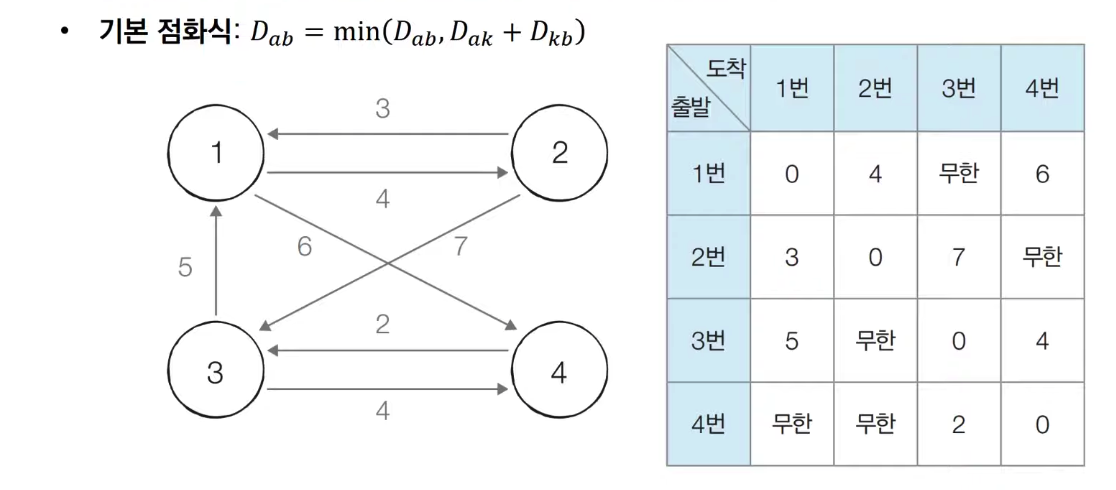
-
1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다
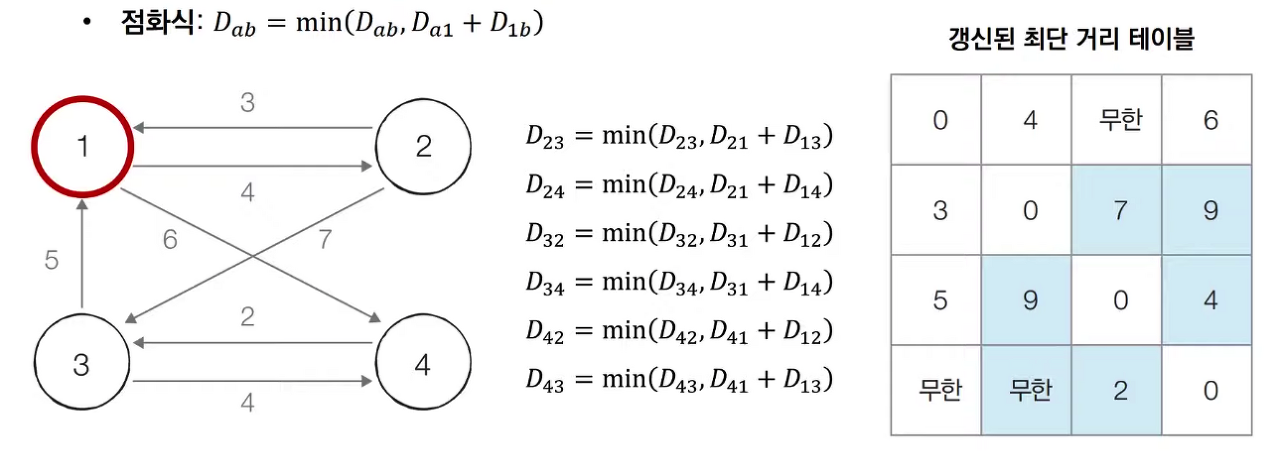
-
2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다
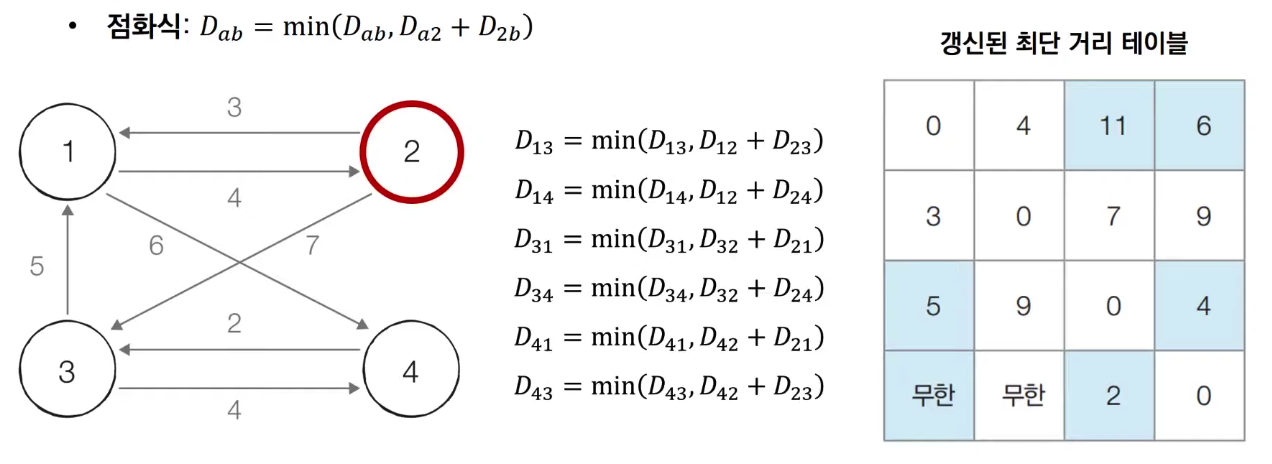
-
3번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다
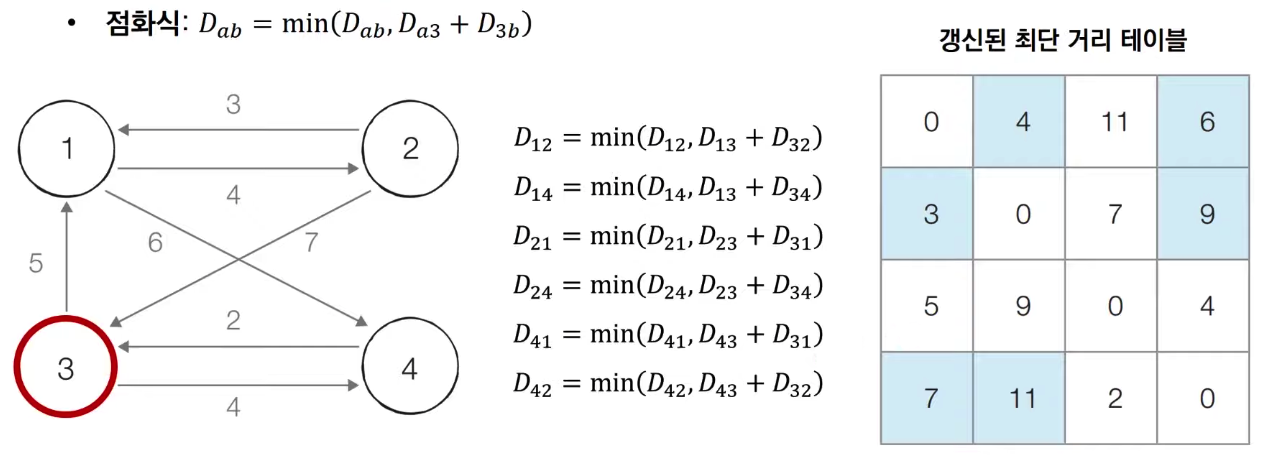
-
4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다
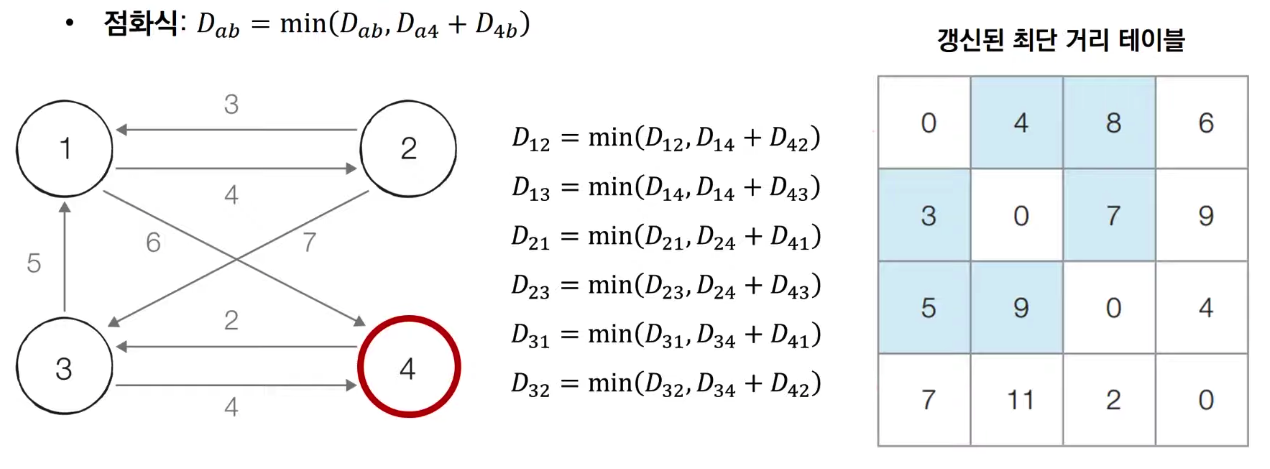
✅ Performance : O(V^3)
✔️ 코드에서 알 수 있듯이 정점의 개수 V만큼 반복분이 3중으로 수행되고 있기 때문에 O(V^3)의 시간 복잡도를 갖는다.
// 점화식에 따라 플로이드 워셜 알고리즘을 수행
for (int k = 1; k <= n; k++) {
for (int a = 1; a <= n; a++) {
for (int b = 1; b <= n; b++) {
graph[a][b] = Math.min(graph[a][b], graph[a][k] + graph[k][b]);
}
}
}