Graph - MST, Prim, Kruskal

🌲 Spanning Tree

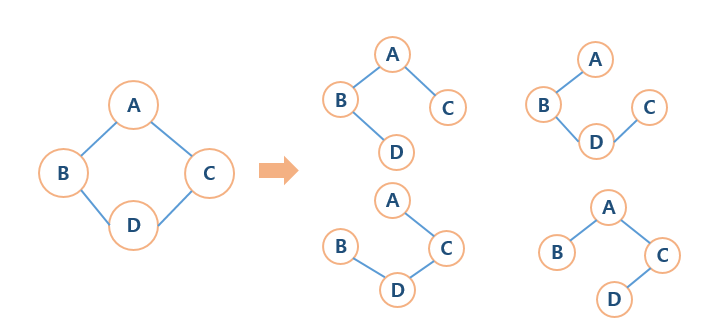
• 그래프의 모든 노드를 포함하는 트리
• 그래프에서 일부 간선을 채택하여 만든 그래프
  => 하나의 그래프에선 여러 개의 신장 트리가 나올 수 있다

✔️ 트리의 특수한 형태로, 사이클이 있어서는 안된다 !

🌲 Minimum Spanning Tree

최소신장트리는 특정 그래프의 신장트리 중에 가장 최소의 weight을 가지는 신장트리를 뜻한다.

✔️ MST를 만드는 대표적인 알고리즘

• Prim 알고리즘
• Kruskal 알고리즘

👉🏻 크루스칼 알고리즘은 가중치가 최소인 간선부터, 프림 알고리즘은 가중치가 최소인 정점부터 하나씩 MST에 포함시킨다는 점에서 둘다 그리디 알고리즘으로 분류할 수 있다.

Kruskal 알고리즘

📌 간선을 거리가 짧은 순서대로 그래프에 포함시킨다면?

✔️ 모든 노드의 간선 집합을 비교
✔️ N−1개의 엣지를 구성 시 종료
✔️ 연산 속도는 cycle 형성 검사 속도가 결정

✅ 프로세스

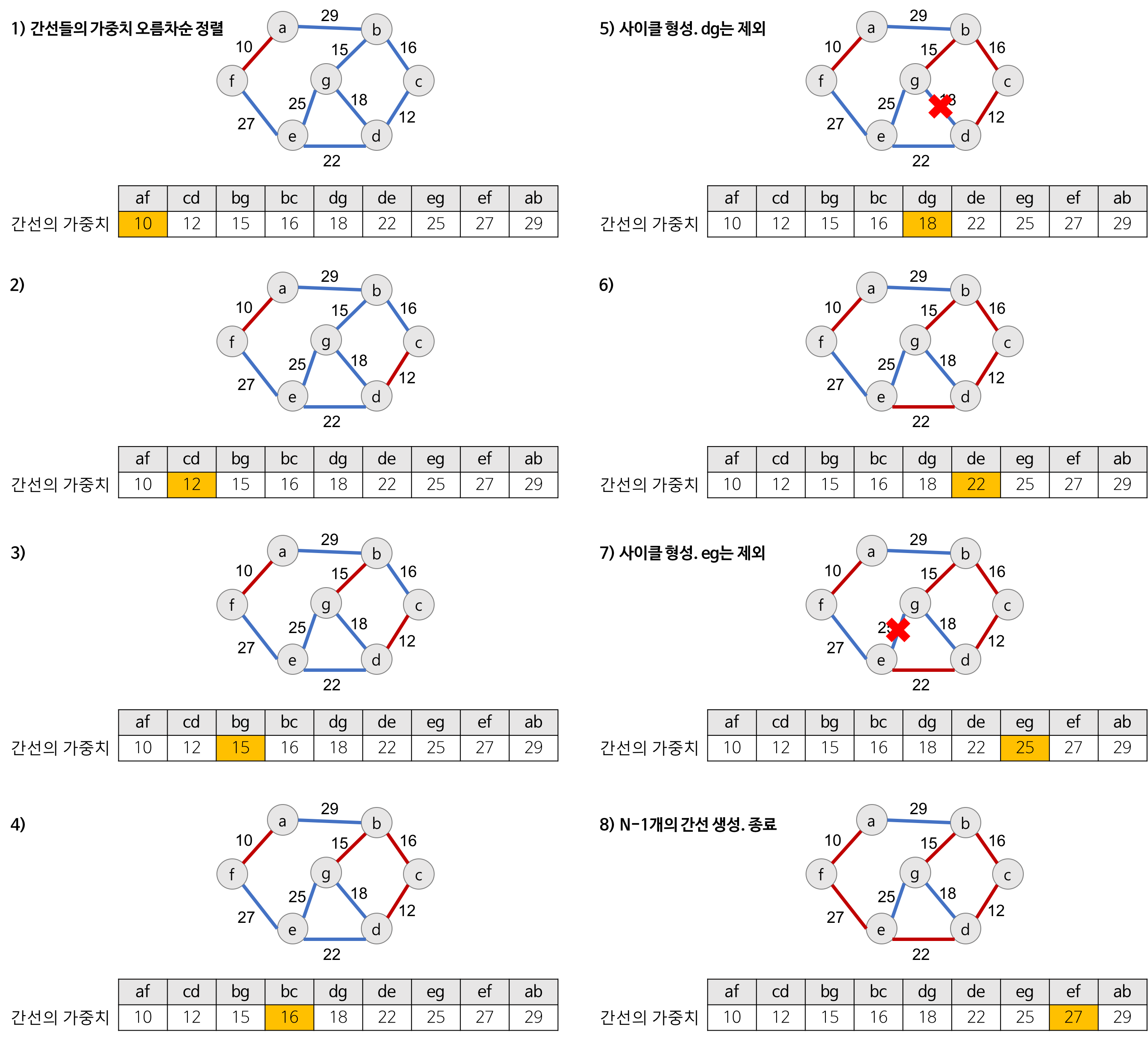
1. 모든 간선들의 가중치를 오름차순으로 연결
2. 가중치가 가장 작은 간선을 선택

• 사이클을 발생시키는지 확인 => 발생시키면 선택 ❌
• 사이클을 발생시키지 않으면 선택

4. 이 과정을 엣지를 n-1개 선택할 때까지 반복

✅ 특징

✔️ 시간복잡도는 edge e의 개수에 따른 O(eloge)의 속도를 가짐

• 초기 edge 오름차순 정렬 O(eloge)
• union-find를 통한 vertex 비교 O(V)
• O(eloe) = O(elogv)와 동일함

✔️ edge 정렬이 속도를 결정짓기 때문에 edge 수가 적은 그래프의 경우 유리

Prim 알고리즘

📌 정점 선택을 기반으로 그래프에 포함시킨다면 ?

✅ 프로세스

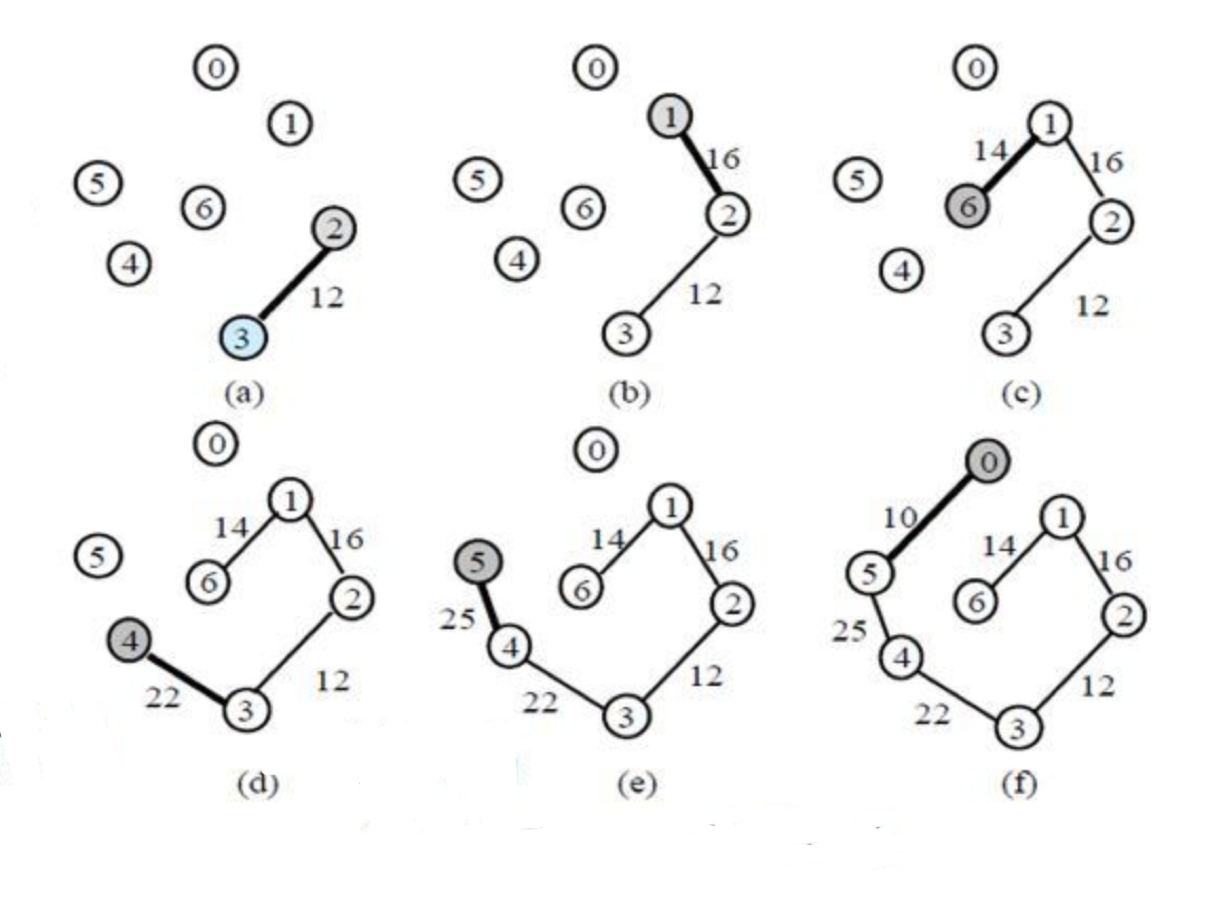
1. 정점들 중 가중치가 가장 낮은 정점을 선택한다.
2. 시작 정점과 인접한 정점들의 가중치를 비교하여 가장 낮은 가중치와 연결한다.

• 이 때 사이클이 형성 된다면 가중치가 낮더라도 제외한다.

3. N개의 노드를 채울 때까지 반복한다.

✅ 특징

✔️ 시간복잡도 :

• 모든 정점의 초기화 O(n)
• 최악의 경우 시작 정점 집합과 그렇지 않은 집합의 모든 노드를 탐색 O(n^2)
• 바이너리 힙을 사용해서 우선순위 큐를 구현한 경우 : O(elogv)

Kruskal vs Prim

✅ Kruskal

• 간선 위주의 알고리즘
• 시작점을 정하지 않음
• 간선을 기준으로 정렬하는 과정이 오래걸림
  => 간선의 개수가 적은 경우 ⭕️

✅ Prim

• 정점 위주의 알고리즘
• 시작점을 정함
• 최소 거리의 정점을 찾는 부분에서 성능에 영향을 받음
  => 간선의 개수가 많은 경우 ⭕️

참조 : https://velog.io/@agugu95/Kruskals-Algorithm%ED%81%AC%EB%A3%A8%EC%8A%A4%EC%B9%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://velog.io/@agugu95/Prims-Algorithm%ED%94%84%EB%A6%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98