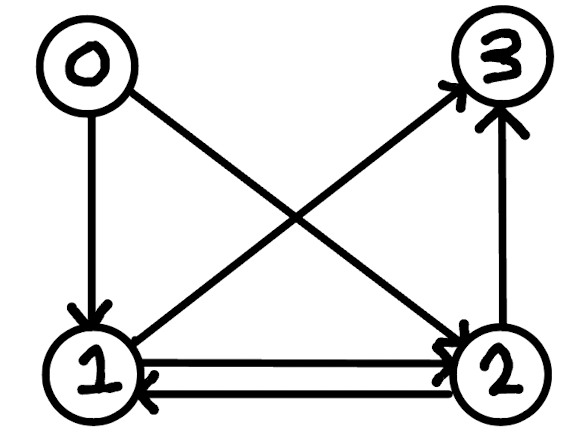
위와 같은 순환 가능성이 있는 그래프가 있을 때
0에서 출발해서 3까지 갈 수 있는 모든 경로
[0, 1, 3]
[0, 2, 3]
[0, 1, 2, 3]
[0, 2, 1, 3]을 구하는 방법을 알아보자.
메인 함수
일단 여러 알고리즘을 사용해보기 전에 메인 함수를 정의했다.
간단하게 위 사진의 그래프 모양을 인접 리스트로 표현하고, 구한 경로들을 출력하는 코드이다.
앞으로 findPath 만 여러가지 방식으로 구현하면서 가능한 방법들을 알아보겠다.
import java.util.*;
public class Main {
static int n;
static List<List<Integer>> allPaths = new ArrayList<>();
static List<List<Integer>> graph = new ArrayList<>();
public static void main(String[] args) {
n = 5; // 도시 수
for (int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
graph.get(0).add(1);
graph.get(0).add(2);
graph.get(1).add(2);
graph.get(1).add(3);
graph.get(2).add(1);
graph.get(2).add(3);
// 시작 도시(0)에서 목표 도시(3)로 향하는 모든 경로를 찾음
findPaths(0, 3);
for (List<Integer> path : allPaths) {
System.out.println(path);
}
}
static void findPaths(int start, int end) {
// 알고리즘 구현
}
}1. BFS
findPaths 함수를 bfs 로 구현해보자.
보편적인 bfs 와 다른 점
- Queue 에 노드의 번호가 아니라 경로 전체를 저장한다.
boolean [] visited를 통해 방문 처리 하는것이 아니라!currentPath.contains(next)로 방문 한 적 있는지 검사한다.- visited 를 써버리면 한가지의 경로만 구하면 끝나버린다. 단순히 노드에 대한 방문 처리로는 모든 경로를 구하는 것이 불가능하다.
static void findPaths(int start, int end) {
Queue<List<Integer>> queue = new LinkedList<>();
List<Integer> initPath = new ArrayList<>();
initPath.add(start);
queue.offer(initPath);
while (!queue.isEmpty()) {
List<Integer> currentPath = queue.poll();
int lastNode = currentPath.get(currentPath.size() - 1);
if (lastNode == end) {
allPaths.add(currentPath);
}
for (int next : graph.get(lastNode)) {
if (!currentPath.contains(next)) {
List<Integer> nextPath = new ArrayList<>(currentPath);
nextPath.add(next);
queue.offer(nextPath);
}
}
}
}최적화
위 코드는 리스트에 contains() 메소드를 사용하므로 효율적이지 못하다. 이를 개선하기 위해 경로와 방문 정보를 한번에 저장하는 클래스 PathState 를 큐에 사용했다.
static class PathState {
List<Integer> path;
Set<Integer> visited;
PathState(List<Integer> path, Set<Integer> visited) {
this.path = path;
this.visited = visited;
}
}
static void findPaths(int start, int end) {
Queue<PathState> queue = new LinkedList<>();
List<Integer> initPath = new ArrayList<>();
initPath.add(start);
Set<Integer> initVisited = new HashSet<>();
initVisited.add(start);
PathState pathState = new PathState(initPath, initVisited);
queue.offer(pathState);
while (!queue.isEmpty()) {
PathState currentPathState = queue.poll();
List<Integer> currentPath = currentPathState.path;
Set<Integer> currentVisited = currentPathState.visited;
int lastNode = currentPath.get(currentPath.size() - 1);
if (lastNode == end) {
allPaths.add(currentPath);
}
for (int next : graph.get(lastNode)) {
if (!currentVisited.contains(next)) {
List<Integer> nextPath = new ArrayList<>(currentPath);
nextPath.add(next);
Set<Integer> nextVisited = new HashSet<>(currentVisited);
nextVisited.add(next);
PathState nextPathState = new PathState(nextPath, nextVisited);
queue.offer(nextPathState);
}
}
}
}2. DFS
findPaths 함수를 dfs 로 구현해보자.
보편적인 dfs와 다른점
- 백트래킹을 사용하여 최종 정점에 달성할 경우 해당 노드를 경로에서 제거하여 다른 경로도 계속 탐색하도록 함
static void findPaths(int start, int end) {
boolean[] visited = new boolean[graph.size()];
List<Integer> path = new ArrayList<>();
dfs(start, end, visited, path);
}
static void dfs(int current, int end, boolean[] visited, List<Integer> path) {
visited[current] = true;
path.add(current);
if (current == end) {
allPaths.add(new ArrayList<>(path));
} else {
for (int next : graph.get(current)) {
if (!visited[next]) {
dfs(next, end, visited, path);
}
}
}
// 백트래킹: 순회가 끝나는 지점에서 current 방문 취소 및 경로에서 제거
path.remove(path.size() - 1);
visited[current] = false;
}시간복잡도
정점의 개수 V, 간선의 개수 E, 가능한 모든 경로의 수를 K 라고 할 때
두 방법 모두 이다. 다만 K 변수가 최악의 경우에 가 될 수 있어서 단순하게 라고 표현해도 된다.
결론
두 방식 모두 시간복잡도가 동일하므로 생각 나는대로 구현하자.
개인적으로는 bfs 는 직관적이라 이해가 쉽고, dfs 는 코드가 단순한것 같다.
단, 메모리 제한이 빡빡하다면 bfs 는 돌아가기 힘들고, dfs 는 재귀 스택의 깊이 제한이 걸릴 수 있다.
K 는 최악의 경우에 까지 될 수 있으므로 1초안에 동작하려면 V 는 약 20정도까지 밖에 안되는 알고리즘이다.
참고로, 순환이 일어나지 않는 그래프라면 DP 를 사용해서 로 해결할 수 있다.
