구간 트리 (세그먼트 트리)는 특정 구간의 합, 최대값, 최소값 등을 구해야 할 일이 많을 때 사용한다.

구간 트리 (Segment Tree)

특정 구간의 데이터의 합, 최대, 최소 등 계산을 효율적으로 할 수 있다.

• 구간 쿼리 (합, 최대, 최소)

일반 배열은 위 연산을 $O(N)$ 로 수행하는데, 구간 트리는 $O(Log N)$ 으로 수행한다.

단 메모리 공간도 많이 차지하고, 초기화, 단일 원소 갱신 ($LogN$) 등 다른 연산은 배열보다 비효율적이다.

특징

• 완전 이진 트리에 가까움
• 리프 노드 제외 자식이 2명
• 리프 노드 제외 노드의 값은 자식의 값의 합 (또는 최대 최소)

개념

구간의 합을 저장하는 구간트리로 일반 세그먼트 트리의 개념을 알아보자.

인덱스	0	1	2	3	4	5
값	3	5	6	7	2	9

위와 같은 배열을 이를 구간합을 저장하는 구간 트리로 변환하면 다음과 같은 트리가 된다.

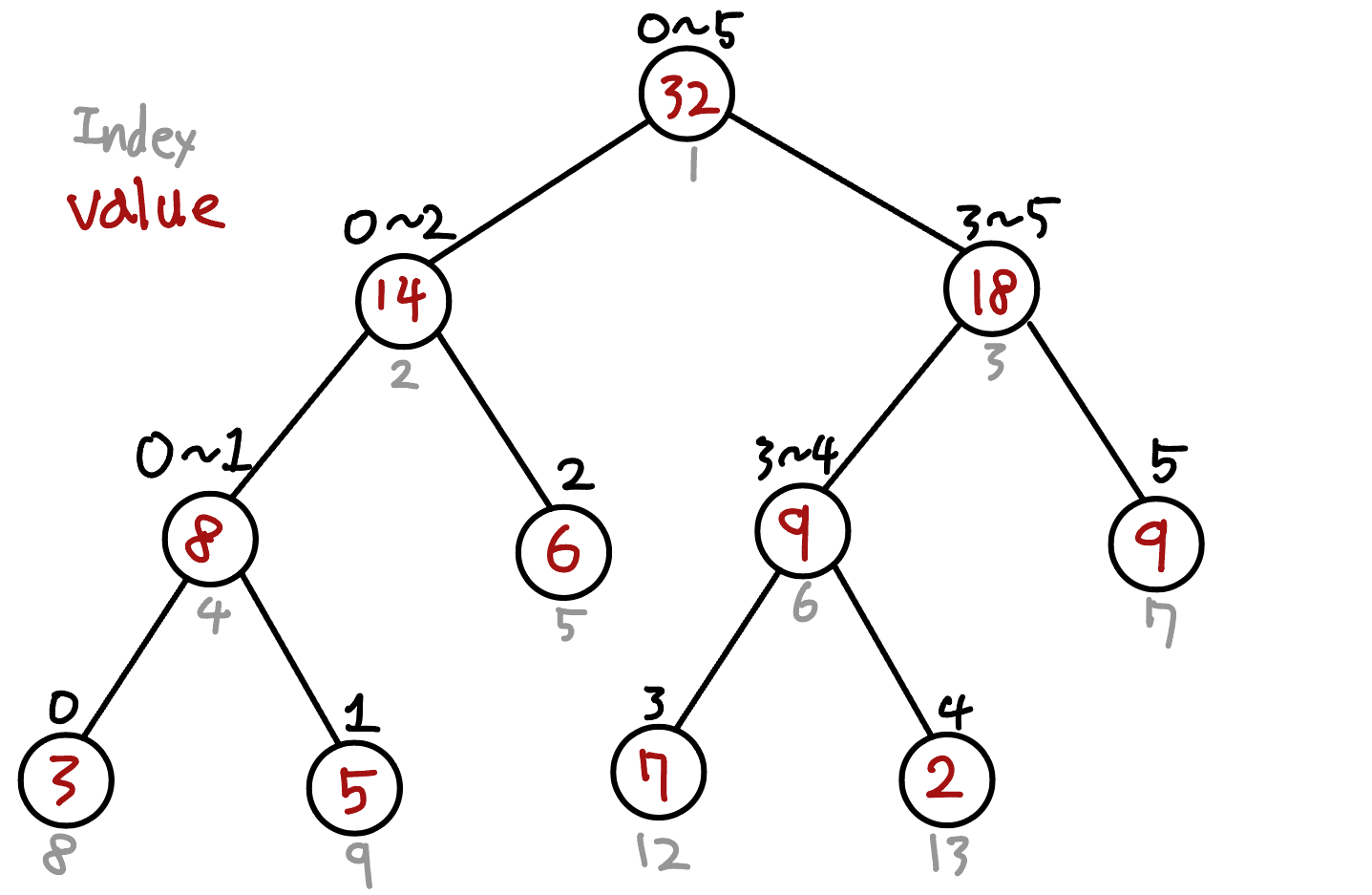
회색은 트리의 인덱스, 검정색 숫자는 원본 배열의 구간 표시, 빨간색 값은 원본 배열의 구간 합 값이다

트리의 루트 노드는 전체 범위(0~5)의 합 (3 + 5 + 6 + 7 + 2 + 9 = 32) 이다.
그 범위를 반으로 나눠서 왼쪽(0~2), 오른쪽(3~5) 으로 나누어 자식 노드로 둔다.
0~2 구간의 합은 (3 + 5 + 6 = 14) 이고, 3~5 구간의 합은 (7 + 2 + 9 = 18) 이다.

트리는 배열에 저장하여 나타낸다. 루트 노드의 인덱스가 1이 되고,
모든 노드의 왼쪽 자식의 인덱스는 node * 2, 오른쪽 자식의 인덱스는 node * 2 + 1 이다.

아래는 위 트리를 나타낸 Tree 배열이다.

인덱스	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
값		32	14	18	8	6	9	9	3	5			7	2

빈 곳은 노드가 존재하지 않는 곳이다.

코드

아래 세개의 함수를 구현해보겠다.

• 트리 초기화
• 단일 값 업데이트
• 구간 합

초기화

원 배열 ary를 사용해서 구간 트리 tree를 만드는 함수이다.

ary는 원본 배열, tree는 트리 배열, node는 현재 트리의 인덱스, start~end 는 현재 노드가 나타내는 원본 배열의 구간이다.

int init(int[] ary, int[] tree, int node, int start, int end) {
    if (start == end) {
        return tree[node] = ary[start];
    }

    int mid = (start + end) / 2;
    int leftSum = init(ary, tree, node * 2, start, mid); // 왼쪽 자식
    int rightSum = init(ary, tree, node * 2 + 1, mid + 1, end); // 오른쪽 자식
    return tree[node] = leftSum + rightSum;
}

// 호출 예시
int[] ary = { 3, 5, 6, 7, 2, 9 };
int[] tree = new int[ary.length * 4]; // 트리의 크기는 배열의 약 4배로 잡는다.
init(ary, tree, 1, 0, ary.length - 1);
// tree = { 0, 32, 14, 18, 8, 6, 9, 9, 3, 5, 0, 0, 7, 2, 0, 0 }

다음과 같은 분기 처리가 필요하다.

1. 말단 노드일 경우 (start == end) -> 트리 노드에 원 배열의 값 저장, 반환
2. 말단 노드가 아닐 경우 -> 자식 노드들의 초기화 함수 호출하고 반환값의 합을 트리 노드에 저장

단일 값 업데이트

ary 배열의 특정 값을 변경할때 그것을 구간 트리에도 적용하는 방법이다.

ary[index]에 diff 값을 더한 배열의 세그먼트 트리로 업데이트 하는 함수이다.

// index: ary 에서 바꾸고 싶은 곳의 인덱스, diff: 위치에 더할 값
void update(int[] tree, int node, int start, int end, int index, int diff) {
    if (index < start || end < index) return;
    tree[node] += diff; // 루트에서 내려가면서 index가 현재 범위에 포함되면 더하는 값 더해주기
    
    if (start == end) return;
    int mid = (start + end) / 2;
    update(tree, node * 2, start, mid, index, diff);
    update(tree, node * 2 + 1, mid + 1, end, index, diff);
}

// 호출 예시
update(tree, 1, 0, ary.length - 1, 4, 8); // ary[4] 의 값에 8을 더한 배열의 세그먼트 트리로 업데이트

1. 현재 트리 노드의 배열 합 범위가 index 를 벗어나는 경우 -> 종료
2. 나머지 모든 경우에 트리 노드에 diff 값 더하기
3. 말단 노드일 경우 -> 종료
4. 말단 노드가 아닐경우 자식 노드들의 업데이트 함수 호출

구간 합

배열의 구간 합을 트리를 활용하여 효율적으로 구한다.

// 담당하는 트리의 현재 구간: start ~ end
// 합을 구할 배열의 쿼리 구간: qs ~ qe
int query(int[] tree, int node, int start, int end, int qs, int qe) {
	// 쿼리 구간이 현재 구간과 상관 없는 경우 -> 0 반환
    if (qe < start || qs > end) return 0;
    
    // 쿼리 구간이 현재 구간을 완전히 포함할 경우 -> 이 구간의 합 그대로 반환
    if (qs <= start && end <= qe) return tree[node];
    
	// 나머지 경우: 두 구간이 부분적으로 겹치는 경우 -> 자식 재귀 호출
    int mid = (start + end) / 2;
    int left = query(tree, node * 2, start, mid, qs, qe);
    int right = query(tree, node * 2 + 1, mid + 1, end, qs, qe);
    return left + right;
}

// 호출 예시
query(tree, 1, 1, ary.length - 1, 1, 4); // ary의 0부터 3까지의 합 구하기

1. 쿼리 구간이 현재 트리 노드의 배열 합 범위를 완전히 벗어나는 경우 -> 0 반환
2. 쿼리 구간이 현재 트리 노드의 배열 합 범위를 완전히 포함하는 경우 -> 현재 트리 노드의 값 반환
3. 범위가 겹치는 경우 -> 자식 노드들의 쿼리값 구한 후 합쳐서 반환.
   좌우로 나눌 때 start 와 end 범위만 변경한다. 쿼리 범위는 변경 X

구간 최대/최소 라면 어떻게 바뀌나?

• 초기화 및 구간 쿼리 함수
  left + right 대신에 Math.min(left, right) 이런 식으로 수정하면 된다.

• 구간 업데이트 함수
  기존 값에 더해지는 값 diff 대신에 절대 값 value 를 받고, 범위 내부이고 말단 노드가 아니라면 tree[node] = Math.min(tree[node * 2], tree[node * 2 + 1]); 이런 식으로 노드의 값을 갱신한다.

백준 - 2042 일반적인 세그먼트 트리 연습 문제이다.
백준 - 6549 세그먼트 트리 문제는 대놓고 구간합 구하라고 나오기보다 이런식으로 많이 활용된다.

느리게 갱신되는 세그먼트 트리

일반 세그먼트 트리에서 추가로 구간 업데이트 연산을 빠르게 작동할 수 있는 Lazy Propagation Segment Tree 이다.

일반 세그먼트 트리의 구간 업데이트: $O(NLogN)$
느리게 갱신되는 세그먼트 트리의 구간 업데이트: $O(LogN)$

개념

구간 업데이트로 모든 노드의 값을 한번에 갱신하려면 너무 많은 노드를 방문해야 하는 문제가 생긴다. 따라서 값 업데이트를 해당 함수 실행 시점에 모두 실행하지 않는다.

자식 노드 등 모든 값을 바로 업데이트 하지 않고, lazy 배열에 임시로 저장하여 추후 해당 노드에 접근하게 되면 lazy 배열에 저장된 값을 확인하고 그때 업데이트 값을 반영한다.

따라서 방문하는 노드의 개수가 많이 줄어들어서 효율적으로 수행 가능하다.

코드

이쯤 되면 묶이는 함수가 많아서 클래스로 묶어서 구현을 많이 한다. 클래스로 한번에 구현하겠다.

class LazySegmentTree {
    long[] lazy; // lazy 값 저장할 배열
    long[] tree;
    int size;

    LazySegmentTree(long[] ary) {
        this.size = ary.length;
        this.lazy = new long[size * 4];
        this.tree = new long[size * 4];
        init(ary, 1, 0, size - 1);
    }

    private long init(long[] ary, int node, int start, int end) {
        if (start == end) {
            return tree[node] = ary[start];
        }

        int mid = (start + end) / 2;
        long left = init(ary, node * 2, start, mid);
        long right = init(ary, node * 2 + 1, mid + 1, end);
        return tree[node] = left + right;
    }

	// us ~ ue 구간의 값을 diff 만큼 증가시킨다.
    public void update(int us, int ue, long diff) {
        update(1, 0, size - 1, us, ue, diff);
    }

    private void update(int node, int start, int end, int us, int ue, long diff) {
        propagate(node, start, end); // 현재 노드에 lazy 값이 있을 경우 적용하기 위해 호출

        // 업데이트 범위가 구간과 완전히 벗어날 때
        if (ue < start || end < us) {
            return;
        }

        // 업데이트 범위가 구간을 완전히 포함할 때
        if (us <= start && end <= ue) {
            lazy[node] += diff;
            propagate(node, start, end); // lazy 값을 자식에게 전파시킴
            return;
        }

        // 나머지 경우: 구간이 업데이트 범위를 완전히 포함할 때 또는 범위가 겹칠 때
        int mid = (start + end) / 2;
        update(node * 2, start, mid, us, ue, diff);
        update(node * 2 + 1, mid + 1, end, us, ue, diff);
        tree[node] = tree[node * 2] + tree[node * 2 + 1];
    }

	// qs 부터 qe 구간의 합을 구한다.
    public long query(int qs, int qe) {
        return query(1, 0, size - 1, qs, qe);
    }

    private long query(int node, int start, int end, int qs, int qe) {
        propagate(node, start, end); // 현재 노드에 lazy 값이 있을 경우 적용하기 위해 호출

        // 업데이트 범위가 구간과 완전히 벗어날 때
        if (qe < start || end < qs) {
            return 0;
        }

        // 업데이트 범위가 구간을 완전히 포함할 때
        if (qs <= start && end <= qe) {
            return tree[node];
        }

        // 나머지 경우: 구간이 업데이트 범위를 완전히 포함할 때 또는 범위가 겹칠 때
        int mid = (start + end) / 2;
        long left = query(node * 2, start, mid, qs, qe);
        long right = query(node * 2 + 1, mid + 1, end, qs, qe);
        return left + right;
    }

	// 현재 노드에 lazy 값이 존재한다면 tree[node] 에 그 값을 적용하고 하위 노드가 있다면 lazy 값을 전파시킴
    private void propagate(int node, int start, int end) {
        if (lazy[node] != 0) {
            tree[node] += (end - start + 1) * lazy[node];
            if (start != end) {
                lazy[node * 2] += lazy[node];
                lazy[node * 2 + 1] += lazy[node];
            }
            lazy[node] = 0;
        }
    }
}

중요한 함수는 맨 마지막의 propagate() 이다.
해당 함수는 현재 노드에 lazy 값이 존재한다면 tree[node] 에 그 값을 적용하고 하위 노드가 있다면 lazy 값을 전파시키는 함수이다.

이 함수를 update, query 함수가 실행되면 바로 호출해서 현재 노드에 lazy 값이 있는지 확인하고, 있다면 적용시킨다.

기본 세그먼트 트리와 주요 차이점은 다음과 같다.

1. lazy 값을 저장하는 lazy[]
2. 노드 방문 시 lazy 값이 있다면 propagete() 를 호출한다.
3. propagate() 는 lazy 값이 존재하는지 확인하고 lazy 값을 트리 노드에 값을 반영한 다음 하위 노드에 lazy 값을 전파한다.
4. 구간 업데이트 할 때, 업데이트 구간이 현재 구간을 포함한다면, 하위 노드들의 lazy 값만 증가시킨다. 코드에서는 현재 노드의 lazy 값을 증가시키고 propagate 를 호출하는 방식으로 이를 구현했다.

디테일한 그림과 설명은 다음 블로그에 정리가 잘 되어있다.

03. 느리게 갱신되는 세그먼트 트리

막상 문제를 마주하게 되면 돌아가는 방식을 다 이해하고 있어야 구현할 수 있으므로 미리미리 비슷한 문제를 자주 풀어보자. 코드도 모든 문제가 동일하지 않고 사소한 디테일이 다르게 구현해야 하는 경우가 많아서 돌아가는 방식을 이해하고 있어야 한다.

자주 출제되는 유형은 아니지만 "구간의 합을 빠르게 구한다" 라는 문장 자체는 생소한 느낌은 아니므로 알아둘만 하다.
의외로 한번 이해하면 구현하기는 어렵지 않다.

백준 - 10999 레이지 세그먼트 트리 연습 문제이다. 위에서 구현한 클래스를 그대로 사용해서 풀 수 있다.