그래프 표현
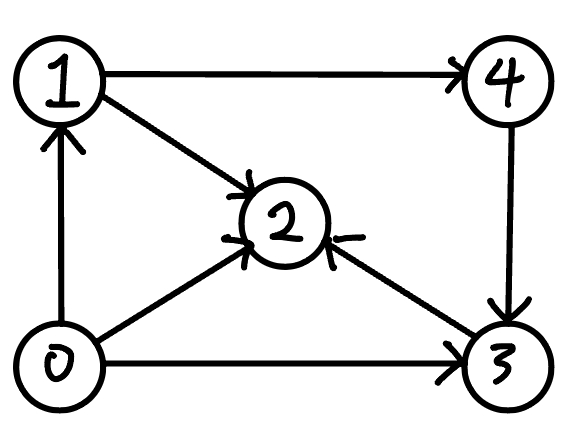
그래프 표현 방식엔 대표적으로 세가지가 있다.
인접 행렬
2차원 배열로 표현한다.
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 |
각각의 행 열을 각각의 정점으로 매핑해서 간선 i 에서 j로 갈 수 있다면 arr[i][j] 에 1 또는 간선의 가중치를 넣는다.
연결되어있지 않으면 0 또는 아주 큰 값을 넣어둔다.
- 장점: 간선 존재 여부 빠름
- 단점: 간선 순회 느림, 메모리 사용량 큼 (V * V)
인접 리스트
2차원 배열로 표현한다.
| i | graph[i] |
|---|---|
| 0 | 1 2 3 |
| 1 | 2 4 |
| 2 | |
| 3 | 2 |
| 4 | 3 |
간선 i 에서 j로 갈 수 있다면 arr[i] 에 j 를 넣는다. arr[i][0] = j 가 될것이다.
연결 리스트 또는 가중치 표현을 위해 클래스를 정의해서 사용한다.
- 장점: 메모리 효율적, 간선 순회 빠름, 일반적으로 알고리즘 작동시간이 효율적임
- 단점: 간선 존재 여부 확인이 느림 (탐색)
간선의 배열
간선을 클래스로 정의해서 1차원 배열 List<Edge>로 표현한다. (Java)
class Edge {
int from;
int to;
int weight;
// ..
}| From | To | Weight |
|---|---|---|
| 0 | 1 | 1 |
| 0 | 2 | 1 |
| 0 | 3 | 1 |
| 1 | 2 | 1 |
| 3 | 2 | 1 |
| 4 | 3 | 1 |
크루스칼 알고리즘 등 간선 중심 알고리즘에서 사용 된다.
그래서 뭘 사용할까
세가지 방법들로 대표적인 그래프 알고리즘을 구현했을떄의 시간복잡도를 보면
(정점의 개수: V, 간선의 개수: E)
| 알고리즘 | 인접 행렬 | 인접 리스트 | 간선 리스트 |
|---|---|---|---|
| BFS / DFS | O(V²) | O(V + E) | O(V + E) |
| 다익스트라 (우선순위 큐) | O(V²) | O((V + E) log V) | O(VE) |
| 플로이드-워셜 | O(V³) | X | X |
| 벨만-포드 | O(V³) | O(VE) | O(VE) |
| 크루스칼 (MST) | O(E log E) + O(V²) | O(E log E) + O(V log V) | O(E log E) |
| 프림 (MST, 우선순위 큐) | O(V²) | O((V + E) log V) | X |
(간선이 많아질 경우 E = V^2 이 되는걸 생각해야 한다.)
- 간선이 매우 많거나 간선의 유무를 매우 많이 확인하는 문제 -> 인접 행렬
- 크루스칼 알고리즘 등 간선 중심 -> 간선의 배열
- 나머지 전부 -> 인접 리스트
문제를 보고 위와 같이 판단해서 알맞은 구조로 구현하자.

