알고리즘 - 소수 판별

KDG·2021년 5월 10일

소수 판별

소수(Prime Number) : 1보다 큰 자연수 중에서 약수가 1과 자기 자신뿐인 수 (1은 제외)
합성수(Composite Number) : 1보다 큰 자연수 중에서 소수가 아닌 수
소수 판별 코드

n = 7
is_prime = True

for i in range(2, n):       # 소수는 1과 자기 자신만 갖기 때문에 2부터 n-1까지의 값만 확인하면 된다.
    if n % i == 0:          # 약수이기 때문에 소수가 아니다.
        is_prime = False   
        break               # 하나의 약수만 나와도 소수가 아니기 때문에 for문을 더 할 필요가 없다.
    
if is_prime:
    print(n, '은 소수입니다.')
    
else:
    print(n, '은 합성수입니다.')

위의 코드를 함수로 만들어서 사용하면 언제든 가져다가 사용할 수 있다.

def isPrime(n):
	for i in range(2, n):
    	if (n % i == 0):
        	return False
    return True
    
# 함수 사용해서 풀기
numbers2 = [127, 1023, 2333, 2337, 8191, 10867, 10869]

for n in numbers2:
    if isPrime(n):
        print(n, '은 소수입니다.')
    else:
        print(n, '은 합성수입니다.')

이렇게 함수를 만들어도되지만 만약 n의 숫자가 엄청나게 커지면 엄청나게 큰 n의 값만큼 for로 하나하나 확인해야해서 처리속도가 느리다는 단점이있다.

약수는 쌍(예를 들어 6의 약수 1, 2, 3, 6의 2,3)을 이루기 때문에 제곱근까지 확인하면 된다.
예를 들어 16이면 1,2,4,8,16인데 16까지 확인하지 않고 4까지만 확인하면 된다.

import math   

def isPrime2(n):
	for i in range(2, math.floor(math.sqrt(n))+1):   # 루트n 까지만 확인
    	if (n % i == 0):
        	return False
    return True
    
# 함수 사용해서 풀기
numbers2 = [127, 1023, 2333, 2337, 8191, 10867, 10869]

for n in numbers2:
    if isPrime(n):
        print(n, '은 소수입니다.')
    else:
        print(n, '은 합성수입니다.')

100까지 소수 구하기

primes = []

for i in range(2, 101):    # 100까지
    if not isPrime2(i):    # isPrime2가 False이면 즉, 합성수이면 무시하고 계속 반복을 진행해라
        continue
    primes.append(i)        # 합성수가 아니면 즉, 소수이면 primes에 추가
    
print(primes)

문제 1

1보다 크고 1000보다 작은 소수는 모두 몇개인가?

primes = []

for i in range(2, 1000):
    if not isPrime2(i):
        continue
    primes.append(i)
    
print(primes)
print(len(primes))

문제 2

1보다 큰 자연수 n이 주어졌을 때, n보다 작은 소수의 개수를 구하는 함수를 만들어보자

import math

def isPrime3(n):
    primes = []
    
    for i in range(2, n):
        check = True
        for j in range(2, math.floor(math.sqrt(i))+1):
            if i % j == 0:
                check = False
                break
                
        if check:    
            primes.append(i)
        
    return len(primes)

** 시간 측정

import time

n = 1000000
start = time.time()
print(isPrime3(n))
elapsed = time.time() - start   # 걸린 시간 = 끝 시간 - 시작 시간

print(elapsed, '초')
print(elapsed/60, '분')
print(elapsed/60/60, '시간')

->
78498
5.638519048690796 초
0.09397531747817993 분
0.0015662552913029988 시간

에라토스테네스의 체

위의 소수를 찾는 코드는 n이 커지면 커질수록 처리속도가 느려진다.
에라토스테네스의 체는 소수를 찾는 또 다른 방법이다.

이미지출처 : https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4

2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
자기 자신을 제외한 2의 배수를 모두 지운다.
남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
자기 자신을 제외한 3의 배수를 모두 지운다.
남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
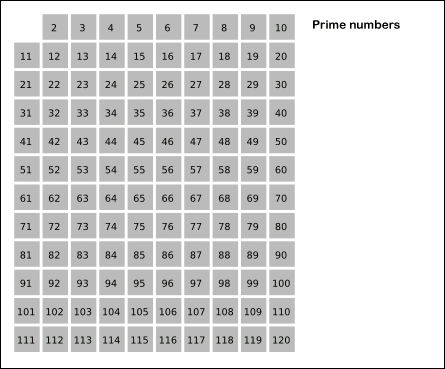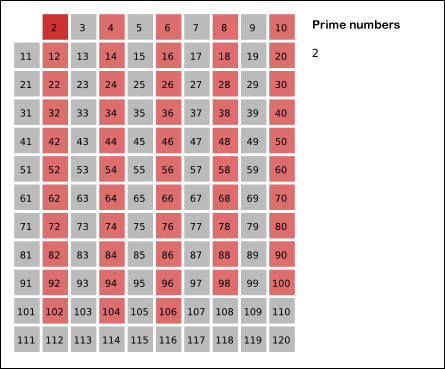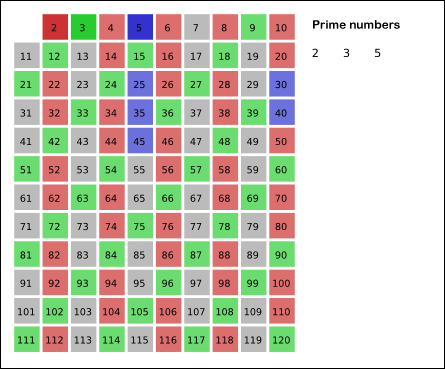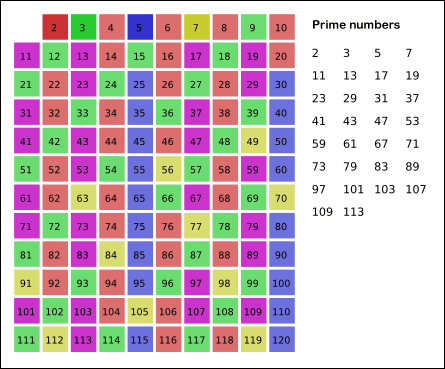
자기 자신을 제외한 5의 배수를 모두 지운다.
남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
자기 자신을 제외한 7의 배수를 모두 지운다.
위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.

def Eratosthenes(n):
    sieve = [False, False] + [True] * (n-1)  # 0과 1은 소수가 아니므로 기본적으로 False로 두고 나머지는 True로 초기값을 준다.
    primes = []   # 소수값이 들어갈 리스트
    
    for i in range(2, n+1):
        if sieve[i]:             # sieve 리스트의 i번째 값이 True. 즉 소수이면
            primes.append(i)     # primes 리스트에 추가
            
        for j in range(i*2, n+1, i):    # i값의 2배부터 n값까지 배수를 찾는다.
            sieve[j] = False            # i값의 배수들은 제거
            
    return len(primes)

** 시간 측정

import time

n = 1000000
start = time.time()
print(Eratosthenes(n))
elapsed = time.time() - start   # 걸린 시간 = 끝 시간 - 시작 시간

print(elapsed, '초')
print(elapsed/60, '분')
print(elapsed/60/60, '시간')

->
78498
1.3221855163574219 초
0.022036425272623696 분
0.00036727375454372827 시간