배낭문제란 무엇인가?
배낭 문제는 n개의 물건과 각 물건 무게 Weight와 가치 Value가 주어지고, 배낭의 용량이 K일 때, 배낭용량을 초과하지 않고 담을 수 있는 물건의 최대 가치를 찾는 문제이다. 각 물건은 하나씩만 존재한다고 가정한다.
모든 경우를 탐색해야하나?
모든 물건의 조합을 구성하여 완전탐색(Brute-Force)알고리즘을 사용하면 N개의 물건이 존재 하기 때문에, 담는다/안담는다의 경우가 존재하기 때문에 (2^N) 이상의 시간복잡도를 가지게 되어 큰 문제는 해결 할 수 없다.
그렇다면, 탐욕적(Greedy)으로 해결 할 수 없나?
단위 무게당 가치를 계산하여 가장 높은것 부터 담는경우, 물건을 쪼갤 수 있는 Fractional KnapSack Problem의 경우는 최적 해를 구할 수 있지만, 통째로 담는 경우에는 반례가 너무 많아 사용할 수 없다.
그럼 다이나믹 프로그램으로?
다이나믹 프로그래밍(DP)기법을 적용시키기 위해서는 아래 두가지 조건이 만족되는지 살펴보아야 한다.
- 최적 부분 구조 (Optimal substructure): 큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
- 중복되는 부분 문제 (Overlapping subproblem): 동일한 작은 문제를 반복적으로 해결한다.
배낭의 부분 문제를 적용하기 위해, 물건은 하나씩 고려하되 배낭 용량에 따른 최대 가치를 저장해나가는 방식으로 찾는다.
풀이
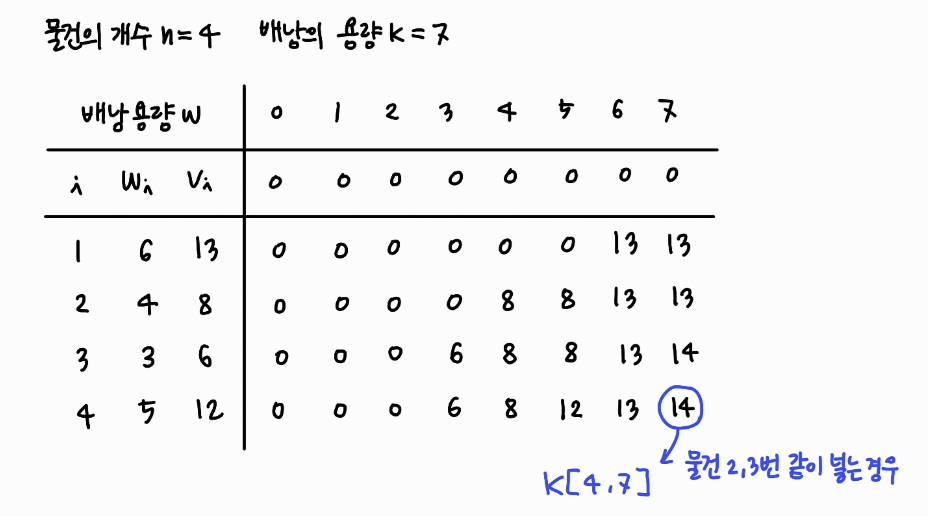
물건을 하나씩 고려해주면서, 현재 배냥의 용량에 해당하는 열, 각각의 물건 갯수에 해당하는 행을 가지는 DP 이차원 배열을 선언해준다.
물건 하나씩 탐색을 시작한다.
이런식으로 선언해주고, 다음과 같은 절차를 통해 기록해준다.
- 물건 i의 무게가 배낭의 현재 임시 용량보다 크거나 담지 않는 경우, 그 전에 있던 최대값을 가져온다. DP[i][j] = DP[i-1][j]
- 물건 i를 배낭에 담는 경우, 현재 무게인 w에서 물건 i의 무게인 wi를 뺀 상태에서 물건을 (i-1)까지 고려했을 때의 최대 가치인 K[i-1, w-wi]와 물건 i의 가치 vi의 합이 K[i, w]가 된다.
연관된 대표 문제
https://www.acmicpc.net/problem/12865
백준 평범한 배낭 문제이다.
이 문제를 풀기 위해서는 위에 설명한 알고리즘을 적용하면 된다.
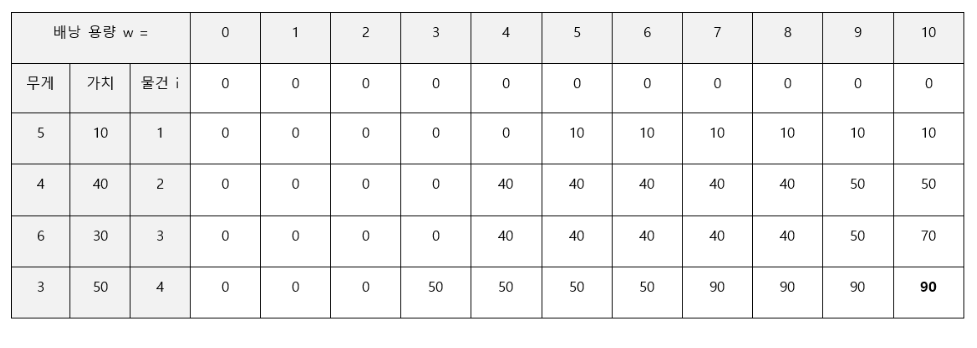
- 예제를 기준으로 다음과 같이 생긴 테이블을 정의한다.
이중 포문을 이용하여, 모든 물건과 모든 용량에 대해 차례대로 탐색하도록 구성하여 DP에는 최댓값이 기록되도록 해준다.
코드
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
arr = [[0,0]]
for i in range(n):
arr.append(list(map(int, input().split())))
dp = [[0]*(k+1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, k+1):
if j < arr[i][0]:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-arr[i][0]] + arr[i][1])
print(dp[n][k])
사진 및 개념 출처 : https://velog.io/@jxlhe46/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%B0%B0%EB%82%AD-%EB%AC%B8%EC%A0%9C-Knapsack-Problem
