[TIL Day4] 파이썬을 무기로, 코딩테스트 광탈을 면하자! (2)

유형별 코딩테스트 대표 문제

1. 힙(Heap)

더 맵게

• 알고리즘의 복잡도
  - 최악의 경우: 수가 하나 남을 때까지 섞어야 하는 경우(n - 1회)
  • 각 단계(섞는 일)에서 요구되는 계산량: 정렬된 리스트에 순서 맞추어 원소 삽입 O(N)
  • 전체 시간 복잡도는 O(N^2)
  • 최소/최대 원소를 빠르게 꺼낼 수 있으면 좋겠다! -> 최소/최대 힙을 이용하자.
• 힙
  - 성질: 최대/최소 원소를 빠르게 상수 시간 O(1)에 찾을 수 있음
  - 연산:
  • 힙 구성(heapify): N개 원소를 삽입할 때 O(NlogN)
  • 삽입(insert): O(logN)
  • 삭제(remove): O(logN)

import heapq

def solution(scoville, K):
    answer = 0
    heapq.heapify(scoville)
    while True:
        min1 = heapq.heappop(scoville)
        if min1 >= K:
            break
        elif len(scoville) == 0:
            answer = -1
            break
        min2 = heapq.heappop(scoville)
        new_scoville = min1 + (min2 * 2)
        heapq.heappush(scoville, new_scoville)
        answer += 1
        
    return answer

2. 동적계획법(Dynamic Programming)

주어진 최적화 문제를 재귀적인 방식으로 보다 작은 문제로 나누어 부분 문제를 풀고, 이 해를 조합하여 전체 문제의 해답에 이르는 방식

• 동적계획법
  - 알고리즘의 진행에 따라 탐색해야 할 범위를 동적으로 결정함으로써 탐색 범위를 한정할 수 있다.

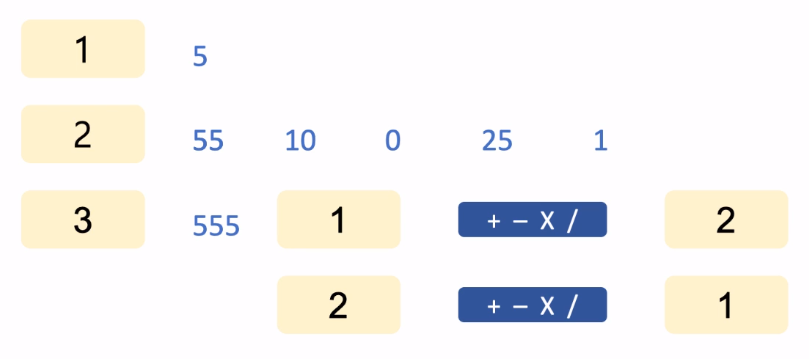
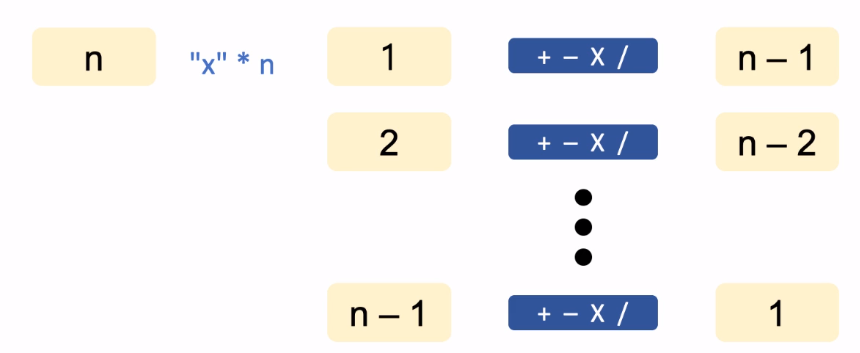
N으로 표현

• 해결 방법
  
  

def solution(N, number):
    # i번 사용해서 만들 수 있는 수들의 집합을 원소로 갖는다
    s = [set() for x in range(8)]
    # 5, 55, 555 ... 를 각 set에 먼저 채워주자
    # enumerate에 start=1 주의하자
    for i, x in enumerate(s, start=1):
        x.add(int(str(N) * i))
        # 이 때 이미 정답이 있는 경우가 있다
        if number in s[i - 1]:
            return i
        
    for i in range(1, len(s)):
        for j in range(i):
            # j번 사용해서 만든 수 중 피연산자 op1을 가져온다
            for op1 in s[j]:
                # i - j - 1번 사용해서 만든 수 중 피연산자 op2를 가져온다
                for op2 in s[i - j - 1]:
                    s[i].add(op1 + op2)
                    s[i].add(op1 - op2)
                    s[i].add(op1 * op2)
                    if op2 != 0:
                        s[i].add(op1 // op2)
        if number in s[i]:
            answer = i + 1
            break 
    else:
        answer = -1
        
    return answer

3. 깊이/너비 우선 탐색(DFS/BFS)

• 그래프
  - 정점(vertex, node)과 간선(edge, link)
  - 유향(directed) 그래프와 무향(undirected) 그래프
  
• 깊이 우선 탐색(DFS; Depth-First Search)
  - 한 정점에서 인접한 모든 (아직 방문하지 않은) 정점을 방문하되,
  - 각 인접 정점을 기준으로 깊이 우선 탐색을 끝낸 후 다음 정점으로 진행
  - 스택을 이용하여 어느 정점에서 dfs를 하고 있는지 기억하고 되돌아간다.
  
  
• 너비 우선 탐색(BFS; Breadth-First Search)
  - 한 정점에서 인접한 모든 (아직 방문하지 않은) 정점을 방문하고,
  - 방문한 각 인접 정점을 기준으로 (방문한 순서에 따라) 또다시 너비 우선 탐색 행함
  - 큐를 이용하여 어느 정점에서 bfs를 해야 하는지를 기록하고 진행한다.
  
  

여행경로

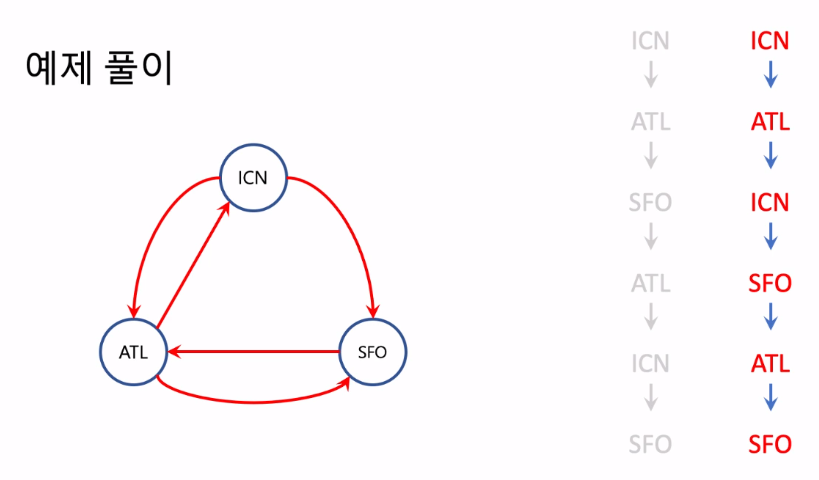
• 해결 방법: 깊이 우선 탐색을 응용
  - 시작 정점은 언제나 'ICN'이고, 모든 정점 방문이 목적이 아닌 모든 간선을 거치는 것이 목적
  - 한 정점에서 택할 수 있는 간선이 두 개 이상인 경우 공항 이름의 알파벳 순서를 따른다.
  - 스택을 이용하여 재귀적인 '한 붓 그리기' 문제를 해결하면 된다.
  • 시간 복잡도는 NlogN (sort() 정렬)
• 그래프의 표현
  - 사전을 이용하여 각 공항에서 출발하는 항공권의 집합을 표현, 출발지를 key로 도착지(의 리스트)를 value로
  - 원소를 꺼내 제거하기 쉽도록 value의 리스트를 알파벳 역순으로 정렬해둔다.
  

def solution(tickets):
    routes = {}
    # key-출발지:value-도착지(리스트)
    for t in tickets:
        routes[t[0]] = routes.get(t[0], []) + [t[1]]
    # 도착지를 알파벳 역순으로 정렬해둔다
    for r in routes:
        routes[r].sort(reverse=True)
    stack = ['ICN']
    path = []
    while len(stack) > 0:
        top = stack[-1]
        # top에서 출발하는 티켓이 없거나, 이미 다 쓴 경우
        if top not in routes or len(routes[top]) == 0:
            # 방문 처리
            path.append(stack.pop())
        else:
            # 스택에 top(다음 출발지가 됨)을 넣고
            stack.append(routes[top][-1])
            # 티켓을 뺀다
            routes[top] = routes[top][:-1]
            
    return path[::-1]