컴퓨터에게 소수점이란

김동현·2023년 11월 22일
무리수소수점실수유리수정수컴퓨터

Question

목록 보기
6/15
post-thumbnail

실수

實 열매 실 數 셈 수
실수란 주로 실직선 위의 점 또는 십진법 전개로 표현될 수 있는 수체계이다.
실수는 무리수와 유리수를 통틀어서 이야기한다.

유리수

유리수란 정수의 비로 나타낼 수 있는 수들이다.

정수
정수란 양의 부호인 +, 음의 부호인 -가 붙어 있는 자연수를 통틀어서 정수라고 말한다.

  1. 자연수 -> 1/1, 2/1, 3/1 ...
  2. 음수 -> -1/1, -2/1, -3/1 ...
  3. 분수와 소수 -> 1/2 = 0.5
  4. 순환하는 무한소수 -> 1/3 -> 0.33333

무리수

정수의 비로 나타낼 수 없는 수들이다.
즉, 순환하지 않는 무한 소수들이다.

  1. √2 -> 1.4142135624...
  2. π -> 3.1415926535....

컴퓨터가 실수를 표현하는 법

정수

정수는 2진수로 변환하여 사용하면 된다.
정수는 할당받은 메모리 공간을 넘어가지 않는 이상, 정확한 값이 보장된다!
1 -> 1
2 -> 10
3 -> 11
4 -> 100

소수점

  1. 소수도 그냥 정수부 표현처럼 이진수로 나눠서 표현 해버리자

😭 이 방법의 경우, 겹치는 숫자가 발생하는 문제가 있다.
1. 1.9 → 1.1001
2. 1.41 → 1.100 and 1

  1. 정수부에서는 2를 나누어 이진법을 표현한다.
    -> 소수부에서는 2를 곱하여 이진법을 표현하자
  1. 0.375 * 2 = 0.75 = 0 + 0.75 => ... 0
  2. 0.75 * 2 = 1.5 = 1 + 0.5 => ... 1
  3. 0.5 * 2 = 1 = 1 + 0 => ...1
  4. -> 0.011

즉 3.75 같은 경우 이진수로는 11.011이 되는 것이다.

컴퓨터에게 무한 소수

일단, 아래와 같은 코드를 실행해 보자

#include <stdio.h>

int main () {
	printf("0.3? %.20f \n", 0.1 + 0.2);
  return 0;
};

console.log(0.1 + 0.2) //0.30000000000000004???

10진법에서 1을 3으로 나누면 0.333333.... 으로 무한히 흘러간다.
2진법에서 0.1(1/10)은 아래와 같은 순환 구조를 띈다.

0.1 2 = 0.2 = 0 + 0.2 => ...0
0.2 2 = 0.4 = 0 + 0.4 => ...0
0.4 2 = 0.8 = 0 + 0.8 => ...0
0.8 2 = 1.6 = 1 + 0.6 => ...1
0.6 2 = 1.2 = 1 + 0.2 => ...1
0.2 2 = 0.4 = 0 + 0.4 => ...0
0.4 2 = 0.8 = 0 + 0.8 => ...0
0.8 2 = 1.6 = 1 + 0.6 => ...1
0.6 2 = 1.2 = 1 + 0.2 => ...1
0.2 2 = 0.4 = 0 + 0.4 => ...0
....

즉, 0.00011001100110011이 무한히 반복되는 케이스가 존재해 버리는 것이다.

이런 순환 소수들을 표현하기 위한 방법으로는 고정 소수점 표현방식과 부동 소수점 표현방식이 존재한다.

고정 소수점 표현 방식

고정 소수점 표현 방식은 할당된 비트 크기를 반으로 잘라 앞은 정수 이진수를, 뒷 부분은 소수 이진수를 넣는 방식이다.

즉, 할당된 메모리 공간을 반으로 나누어 앞부분은 정수부, 뒷부분은 소수부로 채우는 것이다!

만약 빈공간이 발생한다면 모두 0으로 채운다!

⚠️ 여기서 주의할 점은, 제일 앞 비트는 부호를 알려주기 위한 비트로 사용한다.
0이라면 양수를, 1이라면 음수임을 나타낸다!

부동 소수점 표현 방식

浮 뜰 부 動 움직일 동
⚠️ 여기서의 부동은 뜰 부에 움직일 동자를 쓴 부동이다. ⚠️
⚠️ 不(아닐 부)자가 아니다!! ⚠️

부동 소수점 표현 방식은 지수부(exponent)와 가수부(mantissa)로 나뉜다.
지수부는 소수점의 위치를 나타내고, 가수부는 유효한 숫자를 나타낸다.

부동 소수점의 경우 정수부 + 소수부로 표현된 방식을
부호 x 가수(가수부) x 밑수^지수(지수부)로 표현하는 방식이다.

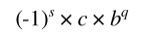
s : 부호부(sign)를 표현하며 0인 경우 +, 1인 경우 -를 나타낸다.
c : 가수부(significand, fraction, mantissa)를 나타내며 양의 정수로 표현된다. 정밀도(precision)에 따라 범위가 달라진다.
b : 밑수(base)/기수(radix)를 나타내며 IEEE 754에서는 2 또는 10이 된다. 이는 각각 2진수, 10진수 표현이 되는것을 의미한다.
q : 지수부(exponent)를 나타내며 지수부는 소수점의 위치를 나타내게 된다.

예를 들면

123.45 -> 123 + 0.45 // 정수부 + 소수부
12.345 -> (-1)^0 x 12345 x 10^3
부호 x 가수 x 밑수^지수

정규화

정규화라는 단어가 많이 있지만, 부동 소수점에서의 정규화란 0보다 크고 밑수보다 작은수.xxx로 표현 될 때까지 지수를 곱하거나 나누는 것이다.

아래의 예시를 보자

십진수의 정규화
12.345 정규화

가수: 12.345
밑수: 10
1. 12 > 10
2. 나누기 10 << 소수점 한자리 올리기
3. 1 < 10
결과: 1.234 * 10^1

이진수의 정규화

십진수 이진수로 변환
3.75

  1. 정수부 이진수 변환
    3 -> 11

  2. 소수부 이진수 변환
    0.375 2 = 0.75 = 0 + 0.75 => ... 0
    0.75     2 = 1.5 = 1 + 0.5 => ... 1
    0.5 * 2 = 1 = 1 + 0 => ...1
    -> 0.011

이진수의 정규화

이진수: 11.011
가수: 11011
밑수: 2
지수: 3

  1. 11 > 10
  2. 나누기 2
  3. 1 < 10
    정규화 결과: 1.1011 * 2^1

이진수: 0.0001100110011...
가수: 0001100110011...
밑수: 2
지수: 무한대

  1. 0.00011
  2. 곱하기 2
  3. 0.0011
  4. 곱하기 2
  5. 0.011
  6. 곱하기 2
  7. 0.11
  8. 곱하기 2
  9. 1.1
    정규화 결과: 1.100110011... * 2^-4

이진수의 정규화시에는 항상 지수부는 1이 될 수 밖에 없다!

IEEE

Institute of Electrical and Electronics Engineers, IEEE
전자 전기 공학 전문가들의 국제 조직 기구이다.

IEEE754는 IEEE에서 개발한 부동 소수점을 표현하는 방법이다.
이는 현재 가장 널리 쓰이는 표준으로 자리 잡았다.

IEEE에서 기본적으로 정의하는 형식은 아래 표와 같다.

TypeSignExponent PartSignificand (Mantissa)Total Number of Bits
Half Precision151016
Single Precision182332
Double Precision1115264
x86 Extended Precision1156480
Quad Precision115112128

bias

1.편견, 편향
2.성향
3.편견, 선입견을 갖게 하다 (=prejudice)

bias는 가만히 내버려 두지 않고 의도적으로 특정 무엇인가를 (다른 것들에 비해) 더 좋아하도록 치우치게 하는 것이다.

컴퓨터에서 bias는 설계자의 의도를 담아 방향성을 주는 것을 바이어스라고 할 수 있다. 이 경우에는 바이어스를 어떻게 거는가 하는 것이 아주 중요한 기술이 된다!

🤔 bias라는 단어에는 어떤 의도가 담겨 있는 것이 핵심이다!

부동 소수점 표현 방식에서 bias

Single Precision(정밀성) 4바이트 실수 저장 공간(float)에서 부동 소수점 표현 방식에서 bias는 127이다.

🤔 왜 127일까?
이유 부터 말하자면 > 양수, 음수를 모두 표현하기 위함이다.

위의 IEEE의 테이블의 정의표를 보면 Single Precision의 경우 정수부는 8비트이다.
8비트는 0~255의 정보를 표현할 수 있다.
이 중 절반을 음의 지수로 활용하기 위해 0~255의 절반의 수인 127을 bias로 잡은 것이다!
-> ✔️ 지수부의 지수는 양수, 음수 모두 나올 수 있다. 10^-1 , 10^1

그렇기에, 양의 지수는 최상의 비트가 1의 값을 갖게 되고, 0과 음의 지수는 최상위 비트가 0이되는 것이다!!

0.1 + 0.2를 구해보자

  1. 0.1

2진수: 0.000110011001100110011001100110011...
정규화: 1.100110011001100110011001100110011... * 10^-4

IEEE 규격:
0/01111011/10011001100110011001100
부호비트: 0(양수)
지수부: bias + (-4) = 127 - 4 = 123 = 01111011
가수부: 뒤의 23자리 = 10011001100110011001100

  1. 0.2

2진수: 0.0011001100110011001100110011001100110011...
정규화: 1.100110011001100110011001100110011... * 10^-3

IEEE 규격:
0/01111100/10011001100110011001100
부호비트: 0(양수)
지수부: bias + (-3) = 127 - 3 = 124 = 01111100
가수부: 뒤의 23자리 = 10011001100110011001100

0/01111011/10011001100110011001100 + 0/01111100/10011001100110011001100

반대로 지수부에서 소수점의 위치를 구하고 더해주면된다!
01111011 > 123 > 123 - 127 > -4 > 0.0001001100...
01111100 > 124 > 124 - 127 > -3 > 0.0010011001...

더하면 0.3이 온다!
0.3 = 0.01011001100110011...

참고 자료

profile
김동현
달려보자
이전 포스트

app.listen

다음 포스트

Node 버전 자동화

0개의 댓글