DFS

그래프의 표현

DFS로 들어가기 전, 그래프의 표현에 대해서 먼저 알아보고 시작하겠다.

구래프 관련 문제 풀이를 하기 위해서는 그래프를 어떻게 구현해야하는지 알아야한다.

엣지리스트

첫번째 엣지리스트, 엣지리스트란 엣지를 중심으로 그래프를 표현한 것이다. 엣지 리스트는 리스트에 출발노드,도착 노드를 저장하여 엣지를 표현한다. 또한 출발노드,도착노드,가중치를 저장하여 가중치가 있는 엣지를 표현한다.

엣지 리스트로 가중치 없는 그래프를 표현해보자.

가중치가 없는 그래프는 출발노드와 도착노드만 표현하기 때문에 리스트의 열을 2개면 충분하다.

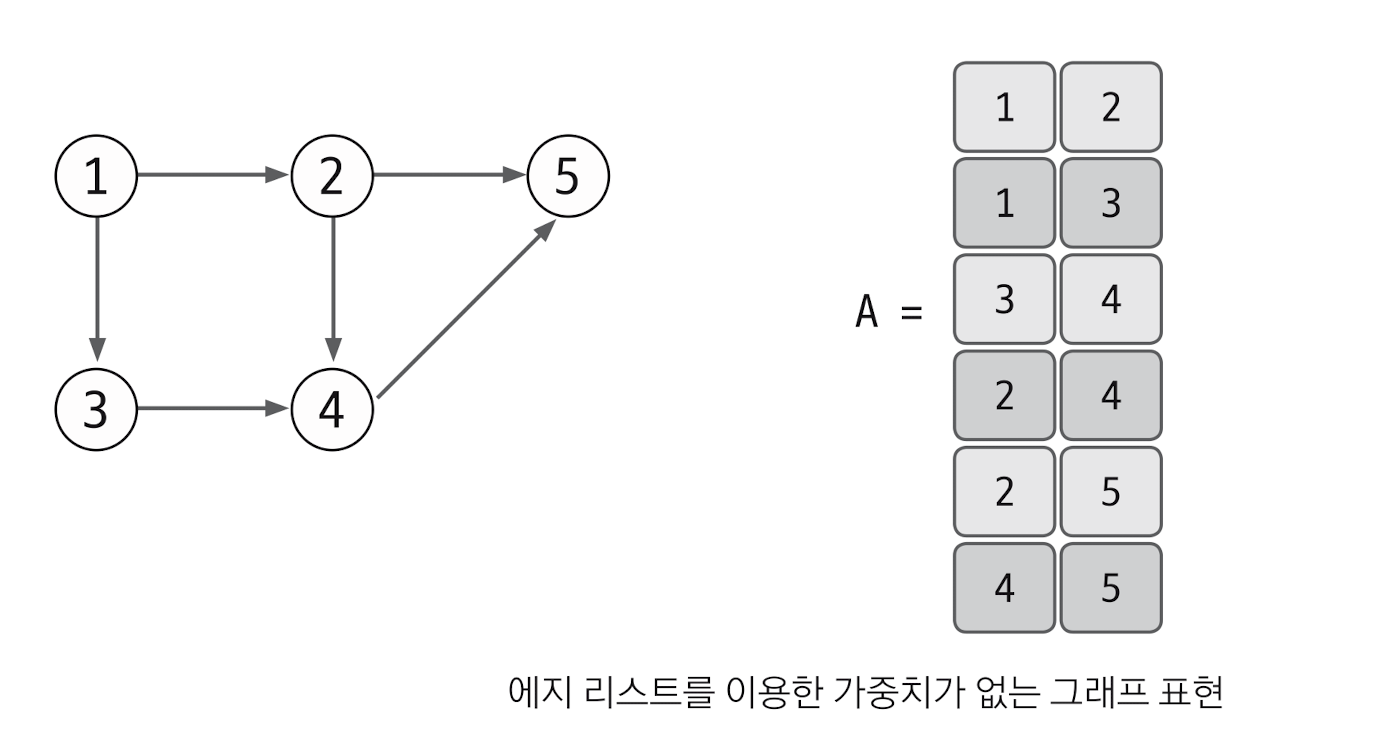
1 → 2 이 [1,2]로 표현된다 . 4→5 는 [4,5] 로 표현된다. 이처럼 방향이 있는 그래프는 순서에 맞게 노드를 리스트에 저장하는 방식으로 표현한다. 그리고 노드를 리스트에 저장하여 엣지를 표현하므로 엣지 리스트라고 한다.

다음은, 엣지리스트로 가중치 있는 그래프를 표현해보자

가중치가 있는 그래프의 경우 열을 3개로 늘려 3번째 열에 가중치를 저장하면 된다.

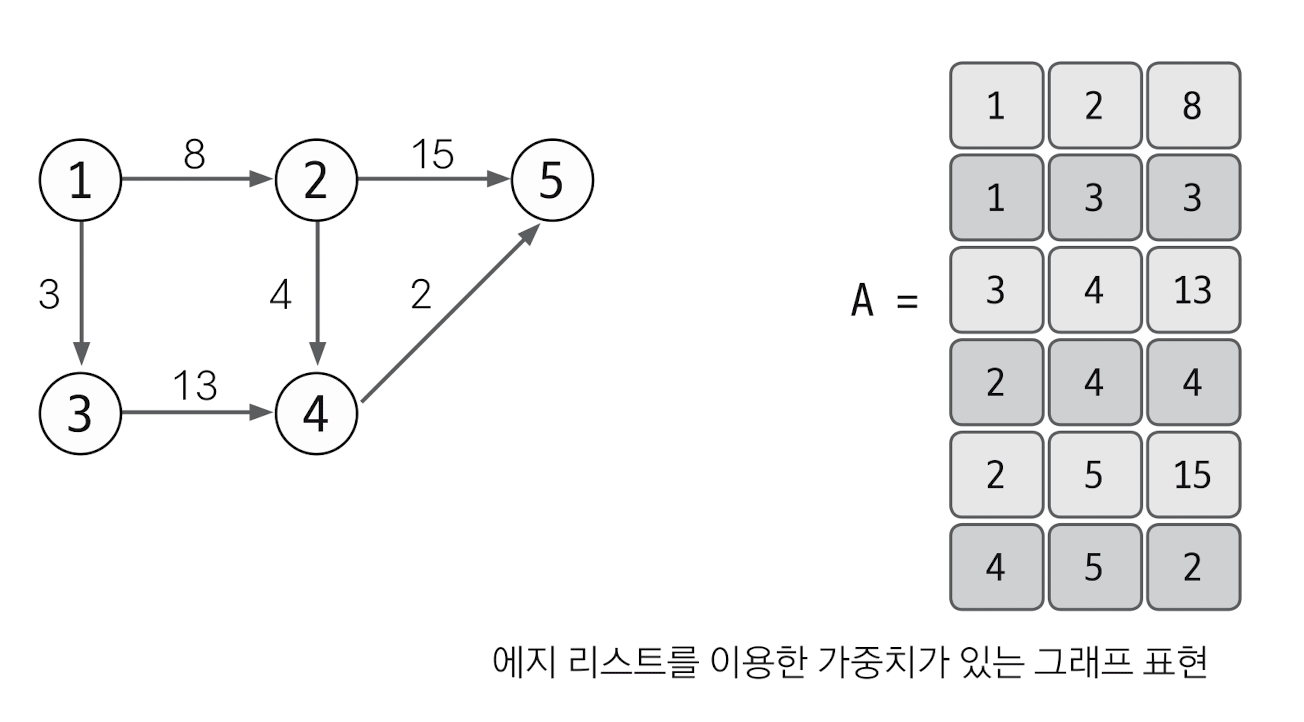
1 → 2로 향하는 엣지에 가중치가 8이 있다는 것을 우리는 [1,2,8] 로 표현한다. 이처럼 어디로 가야할지 방향이 정해진 엣지리스트의 경우 구현하기가 쉽다. 그러나 특정 노드와 관련되어 있는 엣지를 탐색하기는 쉽지 않다.

이러한 엣지리스트는 노드 사이의 최단 거리를 구하는 벨만-포드나 최소 신장 트리를 크루스 칼 알고리즘에 사용한다.

인접행렬

인접행렬의 경우 2차원 리스트를 자료구조로 이용하여 그래프를 표현한다. 인접행렬은 엣지리스트와 다르게 노드 중심으로 그래프를 표현한다. 노드가 5개인 그래프를 5 x 5 인접 행렬로 표현한 다음 그림을 보자.

인접행렬로 가중치 없는 그래프 표현하기

1 → 2로 향하는 노드를 여기에서는 1행 2열에 1을 넣어 표현한다. 1을 넣는 이유는 단순하다 가중치가 있다면 가중치를 넣지만 가중치가 없기 때문에 원소가 들어있다 라는 표현의 1을 넣어준 것이다.

인접행렬로 가중치 있는 그래프 구하기

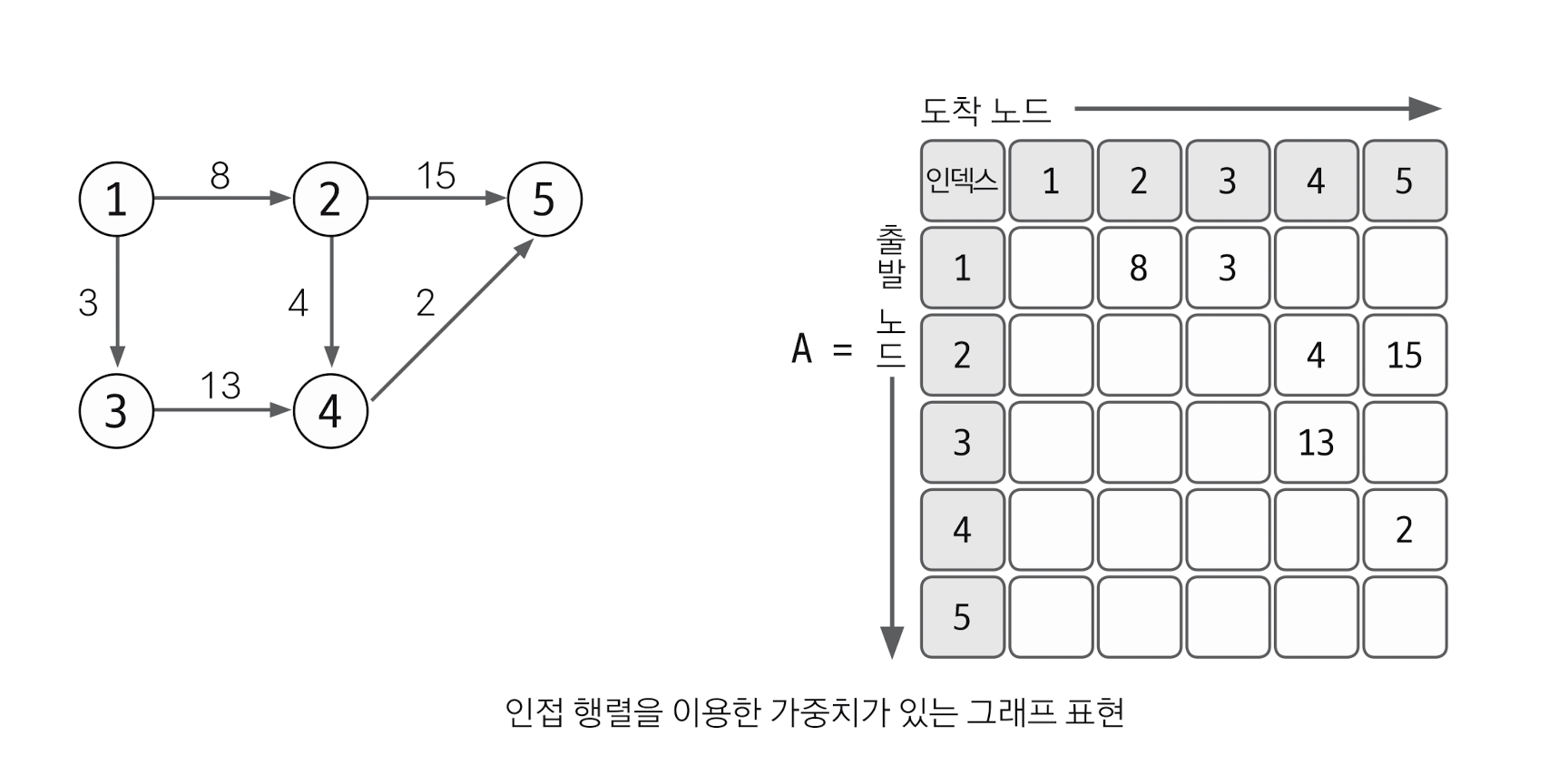
다음은 가중치가 있는 경우의 그래프 표현을 보자. 앞의 가중치가 없는 그래프와 조금 다른 점은 가중치를 기록한다는 것이다. 한번 보자 2 → 5로 향하는 노드가 있고 해당 엣지는 15의 가중치를 가지고 있다. 이것을 행렬에서는 2행 5열에 15를 기록함으로서 표현하고 있다.

이런 방식으로 인접행렬을 이용하여 그래프를 구현하는 것을 매우 쉽다. 두 노드를 연결하는 에지의 여부와 가중치값을 리스트에 직접 접근해서 확인할 수 있다는 장점이 있다.

그러나 노드와 관련되어 있는 에지를 탐색하려면 N번 접근해야하기 때문에 시간 복잡도가 인접 리스트에 비해 느리고 노드 개수에 비해 에지가 적을 때는 공간 효율성이 떨어진다.

인접리스트

인접리스트는 파이썬의 리스트를 이용하여 그래프를 표현한다. 노드 개수만큼 리스트를 선언하여 사용한다. 다음 그림을 통해 인접리스트로 그래프를 표현하는 방법에 대해서 알아보자.

인접리스트로 가중치 없는 그래프 표현하기

다음은 인접리스트로 가중치 없는 그래프를 표현한 것이다.현재의 경우 int 데이터 하나로 그래프를 표현하기에 충분하다. 인접 리스트에는 N 번 노드와 연결되어 있는 노드를 리스트의 index N 에 연결된 노드 개수만큼 리스트에 append 하는 방식으로 표현한다.

이를테면 노드1과 연결된 2,3 노드는 A[1] 에 [2,3]을 연결하는 방식으로 표현하는 것이다.

인접 리스트로 가중치 있는 그래프 표현하기

가중치가 있을 경우 input data를 두개로 한다 (도착노드 , 가중치) 위의 그림은 도착노드와 가중치를 가지고 있는 인접리스트를 표현한 그림이다.

그림을 보면 1과 연결된 노드를 A[1] 에 [(2,8),(3,3)] 로 표현하여 첫번째 튜플 값은 도착노드 두번째 튜플 값은 가중치로 설정하였다.

앞에서 본 인접리스트를 이용한 그래프 구현은 복잡한 편이다. 그러나 노드와 연결된 엣지를 탐색하는 시간이 매우 뛰어나며, 노드 개수가 커도 공간 효율이 좋아 메모리 초과 에러도 발생하지 않는다.

이러한 장점이 있어 실제 코딩테스트에서는 인접 리스트를 이용한 그래프 구현을 선호한다.

DFS

본격적으로 깊이 우선 탐색인 DFS에 대해서 알아보겠다.

DFS의 경우 그래프 완전 탐색 기법 중 하나로, 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘이다.

깊이 우선 탐색은 실제 구현시 재귀 함수를 이용하므로 스택 오버플로에 유의해야한다. 깊이 우선 탐색을 응용하여 풀 수 있는 문제는 다음과 같다.

단절점 찾기

단절선 찾기

사이클 찾기

위상 정렬 등이 있다.

이제, 깊이 우선 탐색이 어떻게 작동하는지에 대해서 알아보겠다.

DFS의 경우 한번 방문한 노드를 다시 방문하면 안되기 때문에 노드 방문 여부를 체크할 리스트가 필요하다. 또한 DFS의 탐색방식은 후입선출 특성을 가지기 때문에 스택을 사용하여 얘기를 해보겠다.

왜 후입선출의 특성을 가지냐고 ? 가장 깊은 노드까지 들어가서 탐색하면서 나올때 보면, 가장 늦게 들어간 노드, 즉 가장 안에 있는 노드가 먼저 탐색된다 이러한 특징을 생각해보면 늦게 들어온 노드가 먼저 나가는 구조를 가지고 있다고 볼 수 있다.

1. DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기.

   

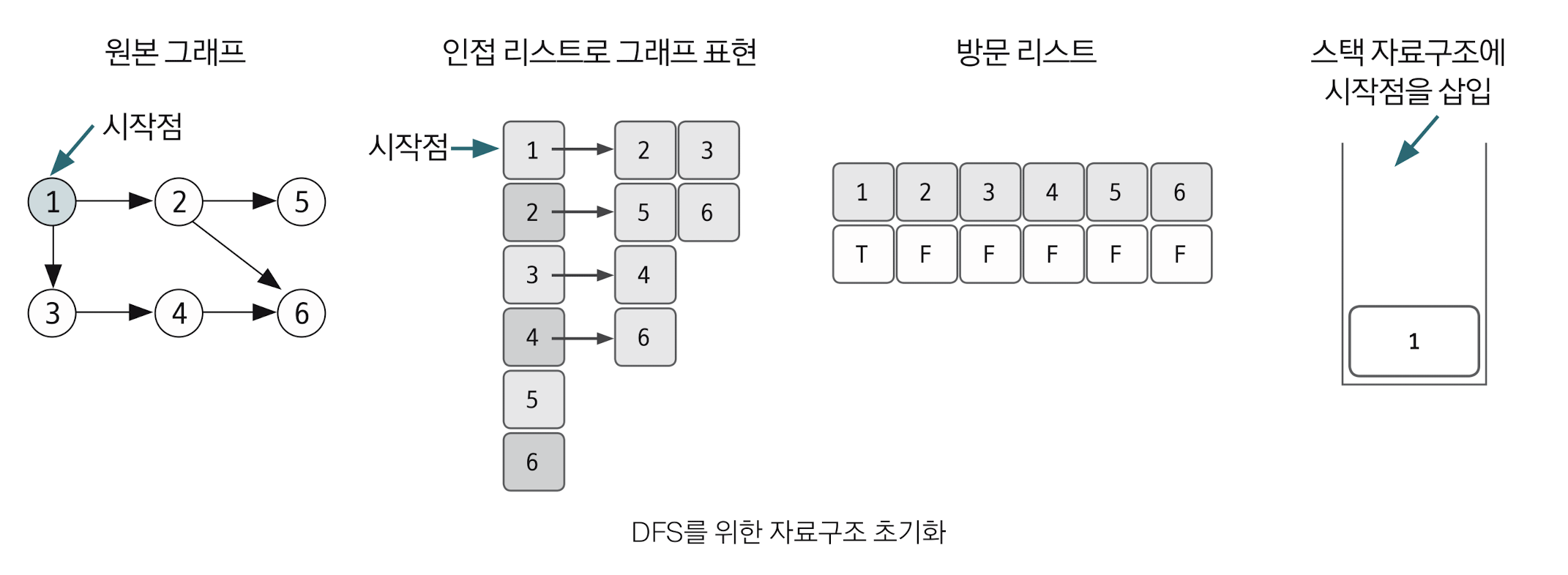
   DFS를 시작하기 전 필요한 초기작업은 다음과 같다

   • 인접리스트로 그래프 표현하기 → 그래프 표현방식은 다른 방식을 선택해도 괜찮다.

   • 방문 리스트 초기화하기

   • 시작 노드 스택에 삽입하기

     스택에 시작 노드를 1로 삽입할 때 해당 위치의 방문 리스트를 체크하면 T F F F F F F 가 된다. 즉, 첫번째 노드는 방문했다는 소리!

2. 스택에서 노드를 꺼낸 후 거낸 노드의 인접 노드를 다시 스택에 삽입하기

이제 pop을 수행하여 노드를 꺼낸다. 꺼낸 노드를 탐색 순서에 기입하고 인접 리스트의 인접 노드를 스택에 삽입하여 방문 리스트를 체크한다. 방문 리스트는 T T T F F F 가 된다 !

3. 스택 자료구조에 값이 없을 때까지 반복하기

   

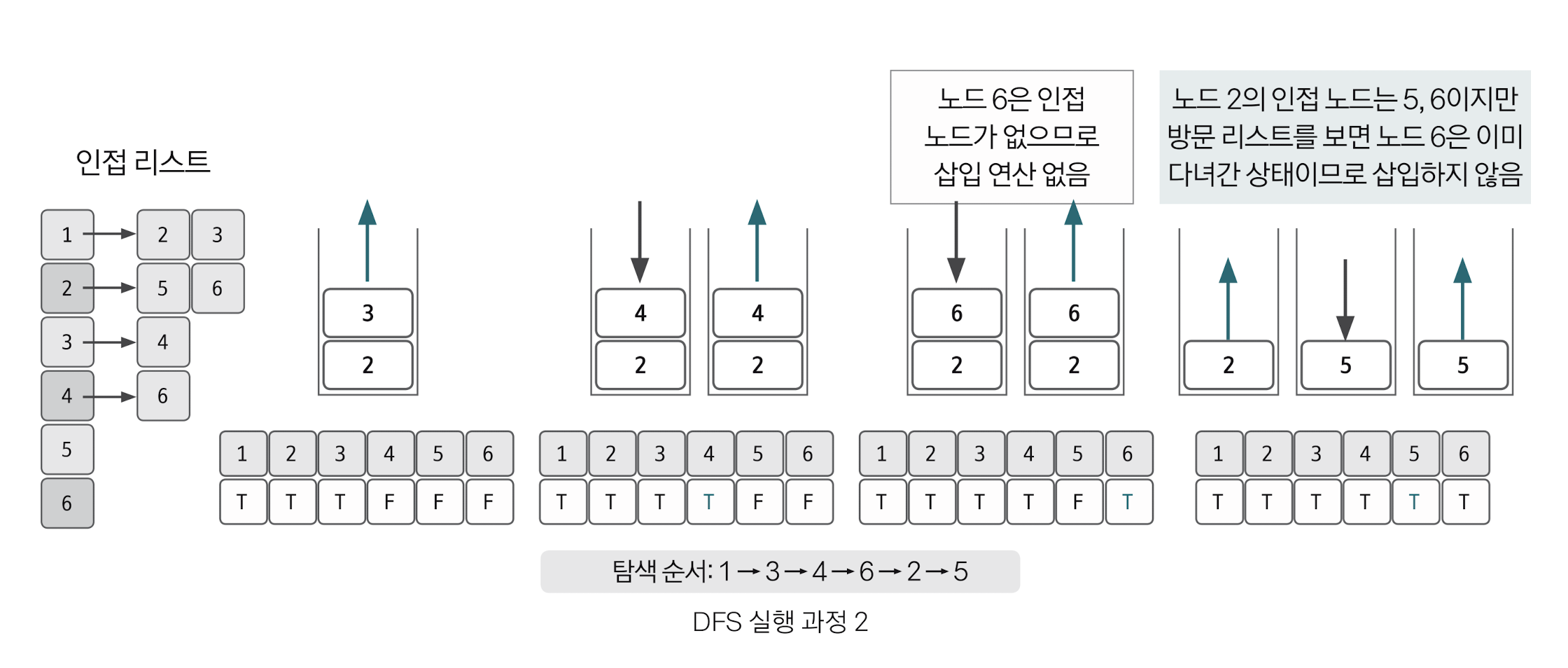
   앞선 과정을 스택 자료구조에 값이 없을 때까지 반복한다. 이때 이미 다녀간 노드는 방문 리스트를 바탕으로 재삽입하지 않는 것이 핵심이다.

구현

## dfs 깊이 우선 탐색 알고리즘
## 재귀를 사용하여 구현
def dfs(node):
    global arr
    visited[node] = True
    print(node)
    for i in arr[node] :
        if visited[i] == False:
            dfs(i)

arr =  [[],[2,3],[5,6],[4],[6],[],[]] # 1부터 시작하도록 초기화
visited = [False] * (len(arr)+1) # 1부터 시작하기 때문에 길이가 + 1

start_node = 1 #시작노드 위치

dfs(start_node)

문제

연결 요소의 개수 구하기

파이썬으로 재귀문제를 풀때 만드시 주의해야 할 점

n(노드개수),m(에지의개수)
arr(그래프 데이터 저장 배열) 초기화
visited(방문정보를 담은 배열) 초기화

DFS:
	visited 리스트에 현재노드 방문처리함 
	현재 노드의 연결 노드 중 방문하지 않은 노드로 DFS 실행 (재귀)

for m(에지의 개수)만큼 반복:
	간선의 양 끝점을 입력받기 때문에 간선의 개수만큼 반복함
	arr 리스트에 그래프 데이터를 저장함

for n(노드의 개수)만큼 반복:
	if 방문하지 않은 노드가 있으면:
		연결되어있으면 연결된것끼리 DFS 한번을 돌기 때문에 연결이 끊긴 부분을 찾음
		연결 요소 개수 값 1증가
		DFS(방문하지않은 노드)

연결 요소 개수 값 출력

import sys
from sys import stdin
sys.setrecursionlimit(10000)

N,M = map(int,stdin.readline().split())
# 노드의 갯수 , 에지의 갯수

arr = [[] for _ in range(N+1)]
visited = [False] * (N+1)
#그래프를 담을 2차원 배열
#방문정보를 담은 boolean 배열

def DFS(v):
    visited[v] = True
    for i in arr[v]:
        if not visited[i]:
            #노드에 방문한적이 없다면
            DFS(i)

for _ in range(M):
    s,e = map(int,stdin.readline().split())
    arr[s].append(e)
    arr[e].append(s)
    #양방향 에지이기 때문에 양쪽에 에지를 더한다

count = 0

for i in range(1,N+1):
    #우리가 그래프를 표현한 방식의 경우 전체 노드만 순회해도 되기 때문에 loop 이용
    if not visited[i]:
        count += 1
        DFS(i)

print(count);

신기한 소수 찾기

모든 자리의 숫자가 소수일 경우를 찾는 문제

예시) 7331소수 , 733 소수 73 소수 7소수

즉, 4자리일 경우 4자리,3자리,2자리,1자리가 모두 소수일 경우 신기한 소수이다.

문제 풀이 전략은 아주 간단하다. 1자리 소수를 일단 먼저 구한다음 1자리 소수에서 2자리로 늘린다 거기서 1~9까지 반복 하며 소수인지 판별한다. 소수일경우 재귀를 타서 다시 3자리로 늘린다 .. 이런 루프를 재귀로 반복하면 N자리 수가 되는 경우가 발생하는데 거기에서 더이상 늘어나지 않도록 if를 걸어 재귀를 종료시켜주면 된다

from sys import stdin

import math

def isPrimeNumber(number):
    if number == 1:
        return False;
    for i in range(2, int(math.sqrt(number)) + 1):
        # x가 해당 수로 나누어떨어진다면
        if number % i == 0:
            return False  # 소수가 아님
    return True  # 소수임

def dfs(number):
    global answer
    global N
    if number < math.pow(10,N) and number > math.pow(10,N-1):
        answer.append(number)

    for i in range(1,10):
        tmp = (number*10)+i
        if isPrimeNumber(tmp) == True:
            dfs(tmp)

N = int(stdin.readline())
answer = []

for i in range(1,9):
    if isPrimeNumber(i) == True:
        dfs(i)

answer = sorted(answer)

for i in answer:
    print(i)

여기서 조금 더 개선을 한다면, 루프에서 짝수일 경우 탐색을 할필요가 없다 ! 불필요한 탐색을 막기 위해서 짝수 일경우를 예외처리하면 좋다. 나는 루프를 그냥 홀수만 돌도록 바꾸었다

from sys import stdin

import math

def isPrimeNumber(number):
    if number == 1:
        return False;
    for i in range(2, int(math.sqrt(number)) + 1):
        # x가 해당 수로 나누어떨어진다면
        if number % i == 0:
            return False  # 소수가 아님
    return True  # 소수임

def dfs(number):
    global answer
    global N
    if number < math.pow(10,N) and number > math.pow(10,N-1):
        answer.append(number)

    for i in range(1,10,**2**):
        tmp = (number*10)+i
        if isPrimeNumber(tmp) == True:
            dfs(tmp)

N = int(stdin.readline())
answer = []

for i in range(1,9):
    if isPrimeNumber(i) == True:
        dfs(i)

answer = sorted(answer)

for i in answer:
    print(i)

친구관계 파악하기

N의 최대 범위가 2000이기 때문에 알고리즘 시간 복잡도 고려할 때 자유롭다 !

이 문제의 경우 5개의 노드가 재귀 형태로 연결되면 1 아니라면 0을 출력하면 된다.

DFS의 시간복잡도 O(V+E) 이다. 인접리스트로 구현 할 경우 각 정점에 연결된 간선의 개수만큼 탐색을 하게 되므로 예측이 불가능하다. 그래서 DFS가 다 끝난 이후를 기준으로 계산해보면, 모든 정점을 한번씩 다 방문하고,모든 간선을 한번씩 모두 검사했다고 할 수 있기 때문에 O(dfs 호출횟수 + 간선) 이다.

import sys
from sys import stdin

sys.setrecursionlimit(10000)
N,M = map(int,stdin.readline().split())

arr = [[] for _ in range(N+1)]
visited = [False] * (N+1)
arrive = False

def dfs(now,depth):
    global arrive

    if depth == 5:
        arrive = True
        #원하는 depth 에 도착하면 그만 순회함
        return
    visited[now] = True
    for value in arr[now]:
        if not visited[value] :
            dfs(value,depth+1)
            # 재귀호출때마다 depth가 1증가
    visited[now] = False
    #재귀호출에서 빠져나올때,현재 재귀보다 더 긴 루트가 있을 수도 있기 때문에 false 처리를 해놓는다
    # True가 되어있으면 순회를 안하니까

for _ in range(M):
    a,b = map(int,stdin.readline().split())
    arr[a].append(b)
    arr[b].append(a)
    #양방향 저장

#인덱스가 정점, value가 정점에 연결된 값

for i in range(N):
    dfs(i,1)
    if arrive:
        break

if arrive:
    print(1)
else :
    print(0)