정렬
정렬 알고리즘
버블 : 데이터의 인접 요소끼리 비교하고, swap 연산을 수행하며 정렬하는 방식
선택 : 대상에서 가장 크거나 작은 데이터를 찾아가 선택을 반복하면서 정렬하는 방식
삽입 : 대상을 선택해 정렬된 영역에서 선택 데이터의 적절한 위치를 찾아 삽입하면서 정렬하는 방식
퀵 : pivot 값을 선정해 해당값을 기준으로 정렬하는 방식
병합 : 이미 정렬된 부분 집합들을 효율적으로 병합해 전체를 정렬하는 방식
기수 : 데이터의 자릿수를 바탕으로 비교해 데이터를 정렬하는 방식
버블정렬
버블 정렬은 두 인접한 데이터의 크기를 비교해 정렬하는 방법이다.
구현은 쉽지만 시간 복잡도는 O(n^2)으로 다른 정렬 알고리즘보다 속도가 느린 편이다.
def bubbleSort(arr):
N = len(arr)
for i in range(N):
for k in range(N-i-1):
if arr[k] > arr[k+1]:
arr[k],arr[k+1] = arr[k+1],arr[k]
return arr
if __name__ == '__main__':
arr = [43,32,24,60,15]
print(bubbleSort(arr))- 비교연산이 필요한 루프 범위를 설정한다
- 인접한 데이터 값을 비교한다
- swap 조건에 부합하면 swap 연산을 수행한다.
- 루프 범위가 끝날때까지 2~3 번 연산을 반복한다.
- 정렬 영역을 설정한다. 다음 루프를 실행할때는 이 영역을 제외한다.
- 비교대상이 없을 때까지 1~5를 반복한다
문제

from sys import stdin
N = int(stdin.readline());
arr = []
for i in range(N):
arr.append(int(stdin.readline()))
for i in range(N-1):
for k in range(N-i-1):
if arr[k] > arr[k+1]:
arr[k],arr[k+1] = arr[k+1],arr[k]
for i in arr:
print(i)
버블정렬의 swap이 한번도 일어나지 않은 루프가 언제인지 알아내야 하는 문제이다. swap이 일어나지 않은 경우 == 모든 데이터가 정렬되었다는 것을 의미한다. 이럴때는 프로세스를 바로 종료하면 복잡도를 줄일 수 있다.
버블정렬의 경우 하나의 원소가 오른쪽으로 이동하는 것은 하나의 루프에서 여러번 발생할 수 있다 그러나, 왼쪽으로 가는 경우는 한 루프에서 한번 발생한다.
왼쪽으로 간 횟수 중 최댓값을 구한다면, 그 횟수는 정렬한 횟수가 될 수 있다.
from sys import stdin
N = int(stdin.readline())
arr = []
for i in range(N):
arr.append((int(stdin.readline()),i))
sorted_arr = sorted(arr)
answer = 0
for i in range(N):
if answer < sorted_arr[i][1] - i:
answer = sorted_arr[i][1] - i
//어짜피 원본 배열의 인덱스는 0,1,2,3,4 ... 로 일정한 숫자의 배열이기 때문에 i랑 비교함
answer = answer + 1
print(answer)선택정렬
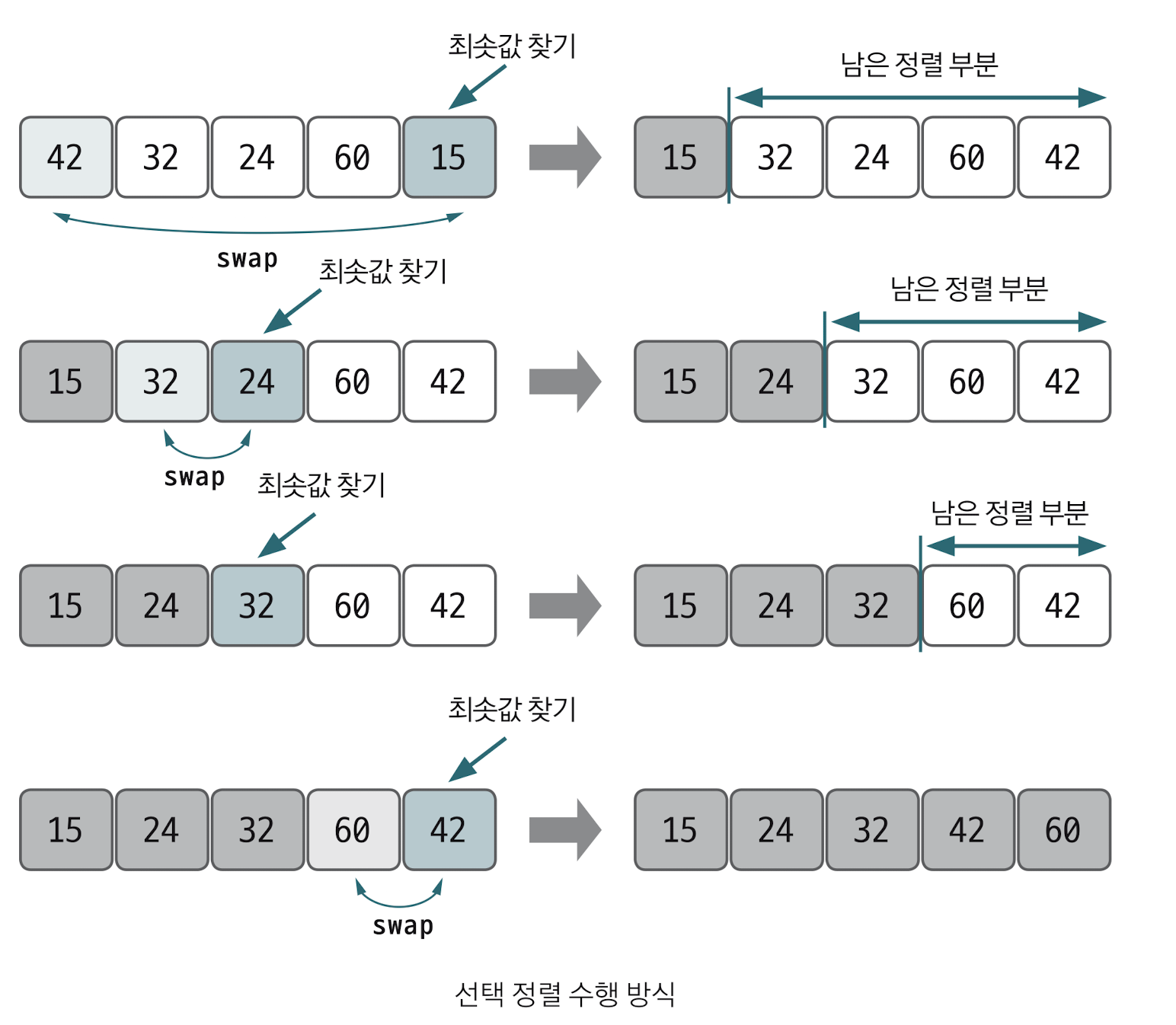
선택정렬은 대상 데이터에서 최대나 최소 데이터를 데이터가 나열된 순으로 찾아가며 선택하는 방법이다. 구현방법이 복잡하고 시간복잡도도 O(n^2)으로 효율적이지 않아 코딩테스트에서는 많이 사용되지 않는다.
선택정렬의 핵심 이론
최솟값 또는 최댓값을 찾고 남은 정렬부분의 가장 앞의 있는 데이터와 swap 하는 것이 선택정렬의 핵심이다.
def selectedSort(arr):
N = len(arr)
for i in range(N-1):
min_idx = i
for j in range(i+1,N):
if arr[i] > arr[j]:
min_idx = j
if arr[min_idx] < arr[i]:
arr[i],arr[min_idx] = arr[min_idx],arr[i]
return arr
if __name__ == '__main__':
arr = [42,32,24,60,15]
print(selectedSort(arr))문제

arr = list(input())
N = len(arr)
for i in range(N):
max_idx = i
for j in range(i+1,N):
if arr[max_idx] < arr[j]:
max_idx = j
if arr[i] < arr[max_idx]:
arr[max_idx],arr[i] = arr[i],arr[max_idx]
print(''.join(str(e) for e in arr))선택정렬을 이용하여 간단하게 풀 수 있다.
위의 선택정렬 알고리즘의 내림차순이 오름차순으로 바뀐것만 다르다.
삽입정렬
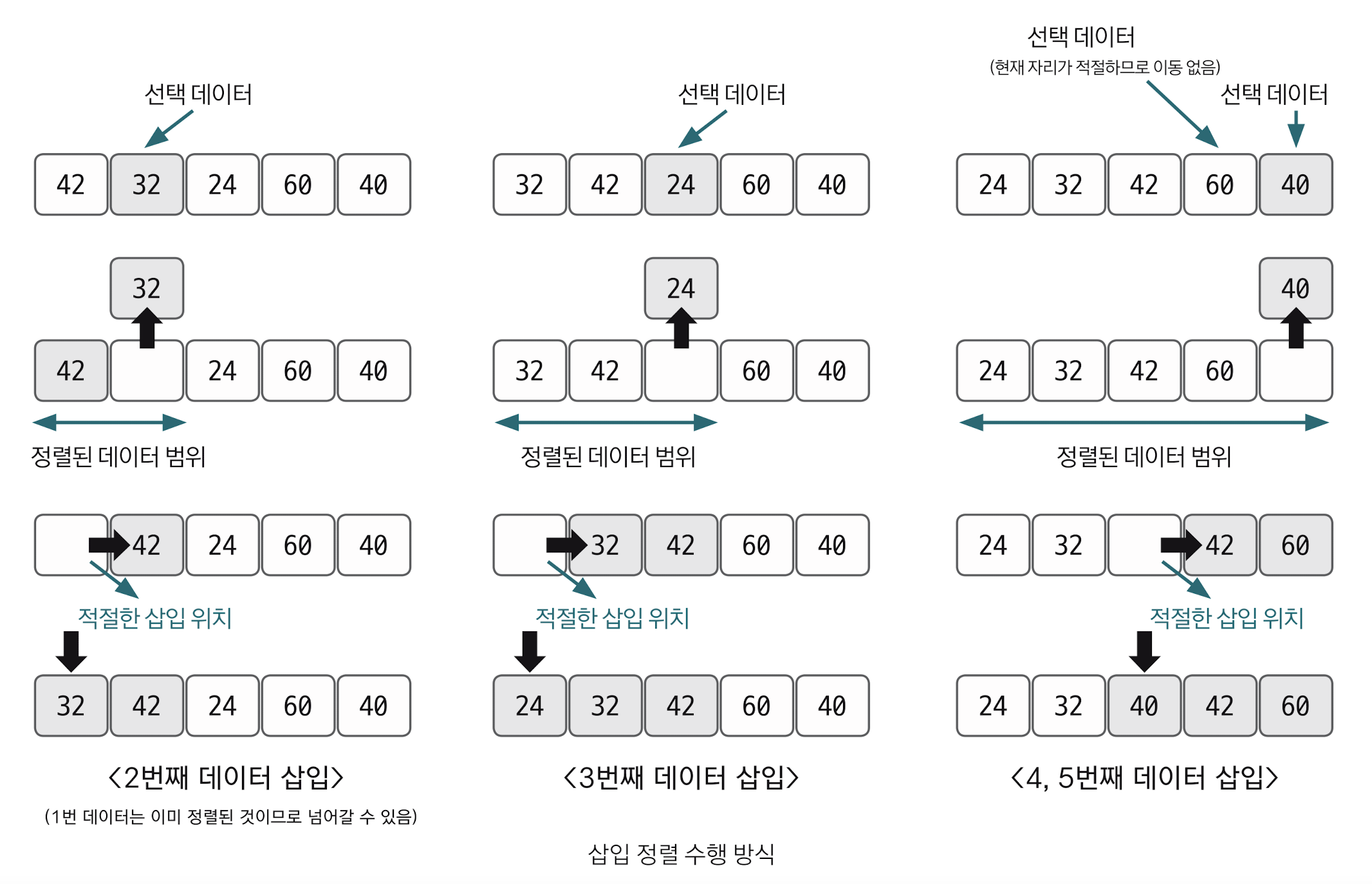
삽입정렬은 이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 방식이다. 시간 복잡도가 O(n^2)로 느리지만, 구현하기 쉽다는 장점이 있다.
선택 데이터를 현재 정렬된 데이터 범위 내에서 적절한 위치에 삽입하는 것이 삽입 정렬의 핵심이다.
def insertSort(arr):
N = len(arr)
for i in range(1,N):
for j in range(i,0,-1):
if arr[j] < arr[j-1]:
arr[j-1],arr[j] = arr[j],arr[j-1]
return arr적절한 삽입 위치를 탐색하는 부분에서 이진 탐색등과 같은 탐색 알고리즘을 사용하면 시간 복잡도를 줄일 수 있다.
이분탐색이란 무엇인가 ?
정렬 된 상태의 구간 내에서 중간에 위치한 원소와 비교하여 중간원소보다 작다면 왼쪽구간으로, 크다면 오른쪽 구간으로 나누어 탐색하는 과정을 말한다.
어떻게 활용하는가
현재의 수를 넣을 위치를 찾는 과정을 이진탐색으로 찾아내면 시간복잡도가 낮아진다.
현재의 수를 key 로 잡아서 이전까지 정렬해두었던 앞의 배열에서 key가 들어갈 자리를 찾는 것이다.
자바 [JAVA] - 이진 삽입 정렬 (Binary Insertion Sort)
문제
해당 문제의 경우 문제 길이가 너무 길어서 간단하게 문제에 대해 설명하고 분석으로 넘어가도록 하겠다.
ATM이 1대밖에 없어서 N명이 모두 해당 자원을 나누어 사용해야하는 상황이다.
이러한 상황에서 각각의 사람이 ATM을 사용하는 시간이 주어진 배열이 있고, 해당 배열을 이용하여 모든 사람이 인출하는데 필요한 시간의 합이 가장 작을 경우를 구하는 문제이다.
이러한 경우 가장 ATM을 짧게 이용한 사람이 먼저 사용하는게 적절하다.
즉, 주어진 ATM 사용시간 배열을 오름차순으로 정렬하는 것이 문제의 해결방법이다.
여기에서 우리는 이 정렬 알고리즘으로 삽입정렬을 사용해보려고 한다.
from sys import stdin
N = int(stdin.readline())
arr = list(map(int,stdin.readline().split(" ")))
for i in range(1,N):
for j in range(i,0,-1):
if arr[j-1] > arr[j]:
arr[j-1],arr[j] = arr[j],arr[j-1]
sum_arr = [arr[0]]
for i in range(1,N):
sum_arr.append(sum_arr[i-1] + arr[i])
print(sum(sum_arr))마지막으로 값을 구하는 과정에서 합배열을 사용하였다.
왜인지는 0~N 번 까지 인출하는데 걸리는 시간을 구하는 과정을 보면 알 수 있다.
0번 손님의 경우 0분 기다리고 , 1분이 걸린다 ⇒ 1분 걸림
1번 손님의 경우 0번손님의 사용시간 만큼 기다려야한다 ⇒ 1 + 2 = 3분 걸림
2번 손님의 경우 0번손님의 사용시간 + 1번손님의 사용시간 ⇒ 3 + 3 = 6분 대기
이런식으로 각각의 손님이 기다려야하는 시간은 다음과 같이 표현할 수 있다.
Wait(i) = Customer(i) + Customer_sum(i-1)
이는, 합배열을 통해 나타낼 수 있기 때문에 합배열로 만들고, 해당 리스트로 sum으로 합쳐주었다.

