기술 통계

모집단(population)

• 통계를 통해 알고 싶어하는 모든 집단
• 모수(parameter) : 모집단의 특성(모평균, 모분산, 모표준편차 등)

표본 (sample)

• 모집단의 분포, 특성을 알기 위해 모집단에서 추출된 일부 집단
• 통계량(statistic) : 표본의 특성 (표본평균, 표본분산, 표본표준편차 등)

추출(sampling)

• 모집단에서 표본을 추출하는 방법

추론(Inference)

• 표본 통계량으로 모집단의 특성을 추론

확률 표본 추출

• 단순 샘플링 (Simple Random Sampling) : 단순 랜덤으로 샘플을 추출
• 층화 샘플링 (Stratified Sampling) : 모집단을 몇 개의 그룹으로 나누어 각 그룹에서 랜덤으로 n개씩 추출
• 계통 샘플링 (Systematic Sampling) : 모집단 데이터에 1~n개의 번호를 임의로 매긴 다음 일정 간격마다 데이터 추출
• 군집 샘플링 (Cluster Sampling) : Cluster로 모집단 데이터로 분할하고, 군집중 하나 or 여러개의 군집을 선정, 선정된 군집의 전체데이터 사용

정규분포

• 정규 분포는 연속 확률 분포 중에서 가장 많이 사용
• 평균에 대해서 좌우 대칭. 평균에서 최대값, 종 모양
• 자연 현상이나 사회 여러 현상들이 정규 분포를 따른다
• 정규 분포는 평균과 표준편차에 의해 결정된다

중심극한 정리

• 표본의 크기가 커질수록 표본 평균의 분포는 모집단의 분포 모양과는 관계없이 정규분포에 가까워진다.
• 표본 평균의 평균은 모집단의 모평균과 같고, 표본 평균의 표준 편차는 모집단의 모 표준 편차를 표본 크기의 제곱근으로 나눈 것과 같다.

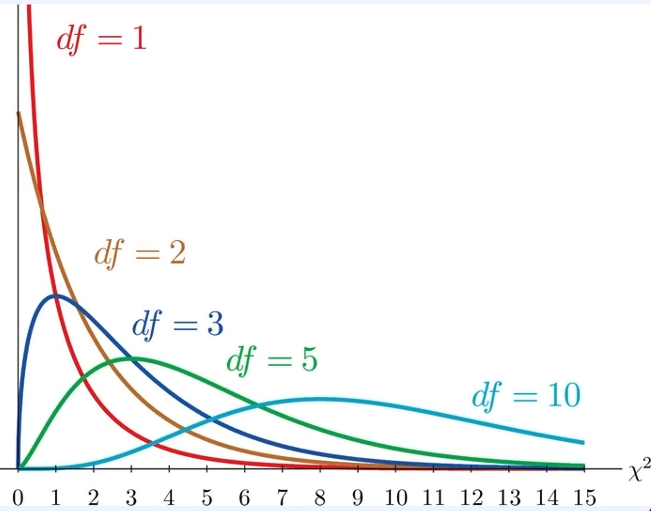
카이제곱분포(chi-squared distribution, x^2 분포)

• 검정 통계량이 카이제곱 분포를 따르는 통계 검정에 사용
• 분산의 특징을 확률 분포로 만든 것
• 분포는 자유도에 의해 정의
• 모분산을 구하는 것
• 카이제곱 분포의 자유도가 높을수록 정규 분포에 근접
• y-skewed(y축에 편향된) 분포
• 제곱된 값의 분산을 다루기 때문에, - 값은 존재하지 않고 + 값만 존재

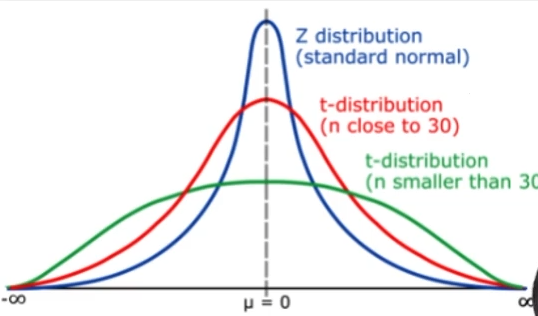
스튜던트 t 분포

• 모분산이 알려져 있지 않고 소규모 표본인 경우에 쓸 수 있는 새로운 분포를 개발
• 정규 분포와 생김새가 비슷하지만, 꼬리 부분이 더 두껍고 길다.
• 표본의 크기가 30 이하인 경우 t 분포 사용
• 모분산을 모를 때 모 평균을 구하는 것
• t 분포는 표본 평균, 두 표본평균 사이의 차이, 회귀 파라미터 등의 분포를 위한 기준으로 사용

F 분포

• 스튜던트 t 분포는 집단 3개 이상은 검정이 불가 -> F분포로 검정
• 카이제곱분포처럼 분산을 다루지만 집단간의 분산을 다룬다.
• 분산분석에 주로 사용
• 집단 간 분산 / 집단 내 분산