퍼셉트론
입력이 2개인 단층 퍼셉트론
- 목표 : input(X)에 대한 Output(y)을 가장 잘 예측하는 Weights(W)를 찾는 것
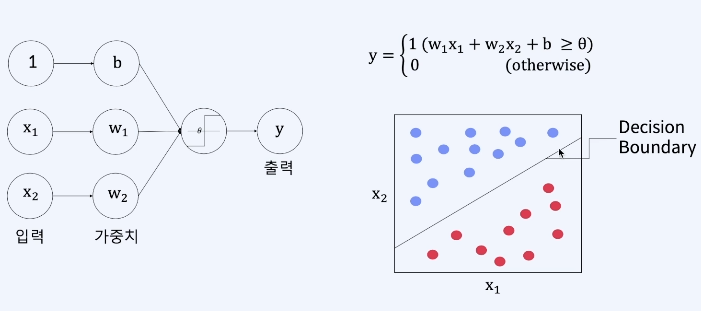
단층 퍼셉트론의 한계 및 XOR
- AND/OR : 하나의 직선으로 분류 가능
- XOR : 하나의 직선으로 분류 불가능
- 최소 두 개의 직선- 곡선
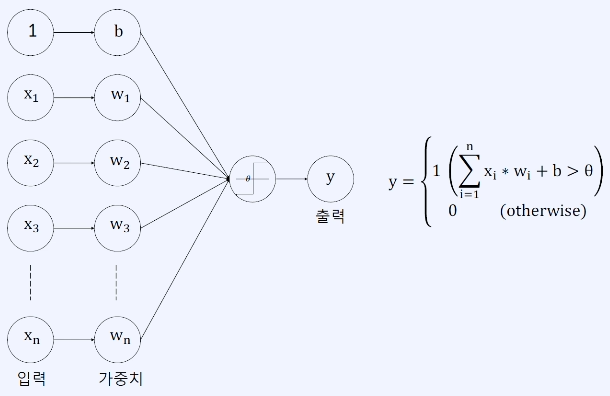
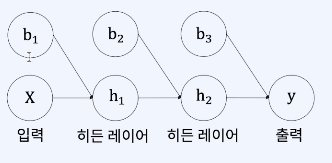
입력이 n개인 단층 퍼셉트론 (MLP)
- 목표 : input(X)에 대한 Output(y)을 가장 잘 예측하는 Weights(W)를 찾는 것
활성화 함수
- 선형 함수 vs 비선형 함수
- 활성화 함수 역할 : 최종 출력값을 다음 레이러로 보낼지 말지 결정하는 역할
선형 함수
Linear 함수 (y=x)
- 입력이 그대로 출력으로 나감
- 네트워크를 쌓는 이점이 없음
- 선형 변환을 통해 다시 WX + B 꼴로 변환 가능
비선형 함수
뉴렬 네트워크에서 층을 쌓는 것의 효과를 보기 위해 사용
Sigmoid
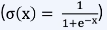
- Logistic function
- 0과 1 사이의 값을 가짐
- 중심이 0이 아님(0.5)
- 주로 히든 레이어에 대한 활성화 함수보다는 2개의 카테고리를 예측하는 출력 레이어에서 사용
Tanh 함수

- -1과 1사이의 값을 가짐
- 중심이 0
ReLU
ReLU(x) = max(0,x))
- 0보다 작은 값을 0으로 설정
- Sigmoid나 tanh보다 학습이 빠름
- 가장 많이 쓰임
Leaky ReLU (Leaky ReLU(x) = max(0.1x, x)
- x가 음수일 때 미분값이 0이 되는 ReLU를 변형하여 약간의 미분값을 갖게 만듦
Softmax
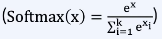
- 주로 레이어 간의 acivation보다는 마지막 layer에서 클래스를 분류하기 위해 쓰임
- 입력 값을 0~1 사이의 값으로 정규화하여 합이 1인 확률 분포로 만듦
손실 함수
모델의 출력이 얼마나 정답(실제 값)과 가까운지 측정하기 위함
- 손실, 즉 모델의 출력 값과 실제 값 간의 차이를 수치화 하는 함수
- 오차가 작을수록 손실 함수 값이 작음
- 손실 함수 값이 작은 방향으로 모델을 학습시키는 것이 목표
- 크게는 회귀를 위한 손실 함수와 분류를 위한 손실 함수로 나뉨
Regression
평균 절대 오차 (Mean Absolute Error, MAE)
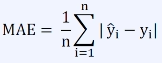
- 모든 데이터(n개)에 대해 예측 값(y')과 실제 정답 값(y)의 차이에 절댓값을 취한 후 평균
- 이상치에 조금 덜 예민함
평균 제곱 오차 (Mean Squared Error, MSE)
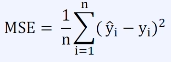
- 모든 데이터 (n개)에 대해 예측 값(y')과 실제 정답 값(y)의 차이에 제곱을 취한 후 평균
- 이상치에 예민함
- 오차가 커질수록 손실 함수가 빠르게 증가
Classification
이진 교차 엔트로피 (Binary Cross-Entropy)
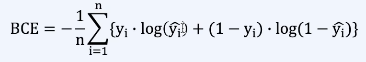
- 이진 분류에 사용 (True/False, 양성/음성 등 2개의 class를 분류)
- 예측값 y'는 0과 1사이의 확률 값
- 예측값이 1에 가까우면 (True or 양성)일 확률이 크고 0에 가까우면 (False or 음성)일 확률이 큼
범주 교차 엔트로피 (Categorical Cross-Entropy)
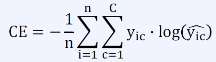
- Class의 수(C)가 3 이상인 분류에 사용
- 예측값 y'는 0과 1사이의 확률 값
- 레이블 y는 one-hot 인코딩 형태
- one-hot 인코딩 : 정답에 해당하는 클래스만 1이고 나머지는 0
최적화 알고리즘
최적화 : 손실 함수를 최소화 하는 Weights(W)를 찾는 과정
- 현재 위치에서 손실 함수의 출력값이 감소하는 방향으로 조금씩 Weights(W)를 움직여 나가는 것
- 산을 내려가는 원리와 같다
- 한 걸음 내딛은 후 그 위치에서 어느 방향이 내리막 길인지 찾아 그 방향으로 한 걸음을 내딛음
- 위의 과정을 더 이상 내려갈 수 없는 곳(최솟값)에 도달할 때까지 반복
- 어떤 방향이 내리막인지
- 한걸음이란 얼마 정도를 의미하는지
Gradient Descent
손실 함수를 최소화하는 Weights(W)를 찾기 위해 기울기(gradient)를 이용하는 방법
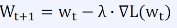
-
어떤 방향이 내리막인가 :
- Gradient
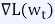
- Gradient
-
한 걸음이란 얼마 정도를 의미하는가 :
- Learning rate, Step size
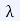
- Learning rate, Step size
-
기울기(Gradient, 일차 미분)가 양수면 w를 감소시키고, 음수면 w를 증가시키는 방식으로 손실 함수가 최소가 되는 지점을 찾음
-
임의의 함수 L의 임의의 점 w에서의 gradient(=L(W))를 계산하면 w로부터 움직였을 때, L값의 변화량을 표현하는 백터가 나옴
-
이 벡터는 가장 가파르게 L값이 증가하는 방향을 가리킨다
-
따라서 반대 방향으로 W를 업데이트 해주면 최솟값을 찾는 방법이 됨
Gradient Descent 문제점
-
모든 파라미터(weights)에 대해 동일한 learning rate를 적용
-
Local minimum, Saddle point에서 빠져나오기 어렵다

-
무조건 기울어진 방향으로 이동하므로 탐색 경로가 비효율적이다.
Learning rate
- 너무 작으면 수렴 속도가 느리고 너무 크면 수렴을 하지 못하고 발산해 버린다.
역전파 알고리즘(Back Propagation)
- input(x)에 대한 output(y)를 가장 잘 예측하는 Weights(W)를 찾기 위해 W를 조정하는 방법
- 출력 -> 입력 순

Sigmoid 미분
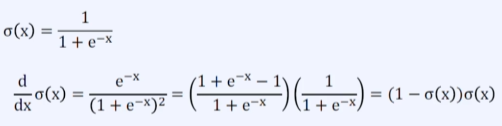
- Sigmoid는 0과 1 사이의 값을 가진다.
- 1보다 작은 값들이 반복되서 곱해지면 거의 0에 가까운 값이 된다
- Gradient가 역전파 과정에서 반복적으로 곱해지며 0에 가까워지는 현상을 Gradient Vanishing이라 부른다
- 이를 피하기 위해 ReLU나 Normalization 등을 사용한다.
최적화 기법
Momentum
- Gradient Descent를 통해 이동하는 과정에 '관성(momentum)을 더함
- 파라미터(Weights)를 업데이트 할 때 현재 뿐만 아니라 이전 gradient도 계산에 포함하여 업데이트
- 과거에 이동했던 방식을 기억하면서 그 방향으로 일정 정도를 추가적으로 이동
- Gradient들의 지수 평균을 업데이트 하는 데 이용
Adagrad(Adaptive Gradient)
- 각 변수마다 step size를 다르게 설정해서 이동하는 방식
- Gradient가 커서 많이 변화했던 변수들은 step size를 작게하자
- 많이 변화한 변수들은 그만큼 학습이 더 많이 되었을 것으로 가정
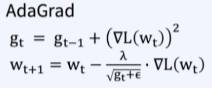
단점
학습을 계속 진행하면 step size가 너무 줄어듦 => 학습을 오래 할 경우 거의 움직이지 않게 된다.
RMSProp
- AdaGrad의 학습이 오래 진행할 경우 step size가 너무 줄어들어 학습이 더 이상 되지 않는 문제를 해결하기 위함
- Gradient의 제곱값을 더해가며 구한 g 부분을 합이 아닌 지수 평균으로 대체
- 변수간 상대적 크기 차이 유지 가능
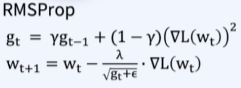
Adam
- RMSProp + Momentum
- 가장 많이 사용되는 최적화 방법
- 지금까지 계산해 온 gradient의 지수평균 저장
- Gradient의 제곱값의 지수평균을 저장
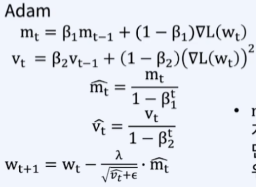
Regularization
과적합(Overfitting)문제를 해결하기 위해 필요하다
과적합(Overfitting)
- 학습 데이터에는 성능이 높지만 검증/테스트 데이터에는 성능이 잘 나오지 않는 경우
- 모델이 복잡하고 데이터가 적을수록 과적합이 일어나기 쉬움
- 학습 데이터가 검증/테스트 데이터를 충분히 대표하지 못할 경우 많이 일어남
- Training loss는 감소하지만 Validation loss는 증가하는 구간
- 모델을 데이터에 과하게 맞추려 하는 경우 - '학습'보다는 '암기'에 가깝다
Mini-batch
전체 데이터를 동일한 크기를 가진 그룹으로 나눈 것Iteration
한 'mini-batch'단위의 데이터를 학습하는 단위Epoch
모든 데이터를 한 번 학습하는 단위
조기 종료(Early Stopping)
- 이전 epoch과 비교하여 validation loss가 감소하지 않으면 학습을 중단
- 바로 전 epoch의 validation loss뿐 아니라 일정한 epoch 수를 거듭하며 validation loss가 감소하지 않으면 학습 중단
- Validation Loss2처럼 loss는 epoch마다 올라가기도 하고 내려가기도 하므로 여러 epoch들에 대해 validation loss추세를 고려
Dropout
- 모델이 복잡할 수록, 뉴럴 네트워크가 커질수록 overfitting에 빠질 가능성이 높음
- Dropout은 위 경우의 문제를 피하기 위한 방법
- 네트워크에 있는 모든 weight에 대해 학습을 하는 것이 아니라 layer에 포함된 weight 중 일부만 학습
- 학습 시 뉴런을 임의의 비율만큼 삭제하며 삭제된 뉴런의 값은 순전파/역전파를 하지 않음
- 하나의 feature에 의전하지 않게 하기 위함
Batch Normalization
한 Batch 단위로 정규화하는 방법
- Batch 단위로 한 레이어에 입력으로 들어오는 값들을 이용해서 평균과 분산을 구함
- 구한 평균과 분산을 이용하여 Normalization을 함
- Learning rate를 크게 설정해도 학습을 안정적으로하여 학습 속도가 개선
- 과적합의 위험을 줄일 수 있다
- Weight 초깃값 설정의 의존성이 줄어듦
- Local minima에 빠질 가능성을 낮춰줌
Internal Covariant Shift
- 레이어를 통과할 때마다 각 레이어나 활성화 함수의 입력값의 분산(분포)이 달라지는 현상
- 학습 시 hidden layer에서 입력 분포가 학습할 때마다 변화하면 weifht가 최적이 아닌 방향으로 학습될 수 있음
- 학습을 불안정하게 하는 요소 - 신경망이 깊어질 수록 학습이 불안정해 진다.
- Batch Normalization의 경우 위와 같은 문제를 해결 가능 - 학습 시 평균과 분산을 조정
- 단순히 평균/분산을 구하고 각각 0/1(unit gaussian)로 만들려는 것이 아니라 Scaling(y)와 Shifting(b)를 통해 적절한 분포를 유지하면서 학습할 수 있도록 도와줌
Gradient Vanishing
- 뉴럴 네트워크 학습을 위한 역전파 과정에서 낮은 레이어로 갈 수록 기울기(Gradient)가 작아지는 현상
- 해결을 위해 Sigmoid 대신 ReLU 사용, 매 layer의 입력을 normalization 해주어 작아지지 않도록 하는 방법이 있다
- 반대로 Gradient가 너무 커지는 현상을 Gradient Exploding이라 하며 Batch Normalization은 Gradient Exploding도 예방하는데 도움이 됨
- Weight의 scale을 정규화하기 때문에 gradient exploding도 방지 가능
