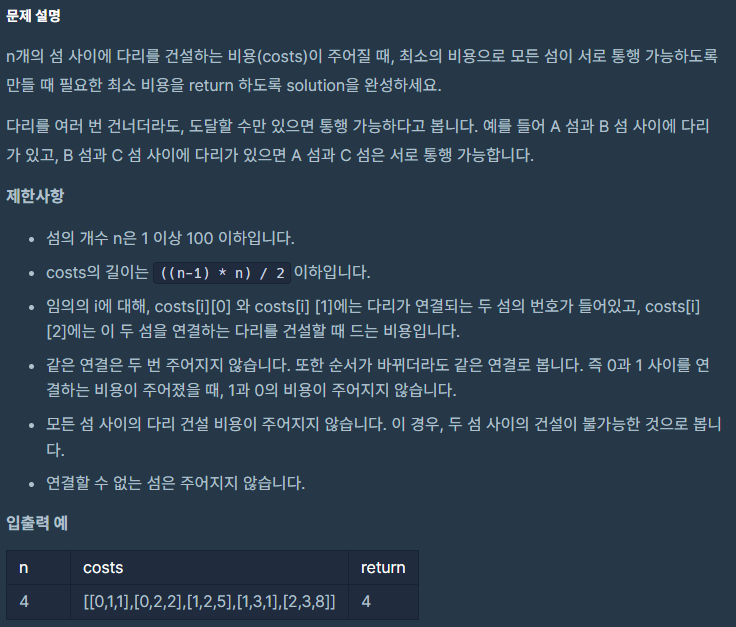
코딩테스트 고득점 Kit > 탐욕법(Greedy)
문제풀이 (2022-02-26 SAT 💻)
🤔 사담
고득점 Kit에는 분류가 명시되어 있어서 해당 문제들을 풀 때에는
만약 내가 분류 유형을 모르고 문제를 접했다면 어떤 방식으로 접근했을까
에 대해 반드시 생각해보는데
처음에는 dfs나 bfs 문제인가? 싶었으나 딱 봐도 커버 불가능한 경로들이 있었다
다음으로는 visited check 하면서 모든 노드가 방문될 때까지
방문하지 않은 노드에 대해서만 다리를 건설하는 식으로 코드를 짜봤는데
이 경우에는 모든 섬이 통행 가능하도록 만들어야 하는 문제의 조건을 충족할 수 없었다
해당 경우의 반례 테케는 질문하기 게시판에서도 찾아볼 수 있었다
📌 cf) https://programmers.co.kr/questions/3981
⭐ 풀이의 핵심
다소 엉뚱한 풀이로 헤매다가 결국 구글링을 통해
MST(Minimum Spanning Tree) 를 활용해 풀어야 하는 문제임을 깨달았다
알고리즘 수업에서 MST를 배웠던 기억은 있는데
실제로 코테 문제에서 활용해본 것은 처음이었다
MST는 Kruskal's Algorithm 또는 Prim's Algorithm을 활용할 수 있다
그림과 수도코드로만 공부했던 알고리즘들이라서
구현 연습해볼 겸 두 가지 방식으로 코드를 짜보았다
➕ 참고 Kruskal's Algorithm
- edge들을 가중치 기준 오름차순으로 정렬
- 가중치가 작은 edge부터 MST에 포함시키되 사이클을 형성하지 않도록 체크
👉 사이클 형성 여부를 확인하는 위해서는
Disjoint Sets 표현을 위해 활용되는 Union-Find 알고리즘을 사용한다
내 블로그에는 Union-Find 알고리즘을 다룬 포스트가 없어서 레퍼런스를 달아두겠다
📌 cf) https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
👉 edge 정렬 부분에서 시간 복잡도가 결정되므로
퀵 정렬과 같은 효율적인 방법을 통해 edge 정렬을 수행한다는 전제 하에
O(ElogE)의 시간 복잡도를 갖는다
➕ 참고 Prim's Algorithm
- 임의의 시작 node를 선택
- 해당 node와 인접한 node 중 최솟값을 갖는 edge로 연결된 node를 선택하여 MST에 포함
- MST에 모든 node가 포함될 때까지 (n-1개의 edge가 포함될 때까지) 위 과정을 반복
👉 인접 node들을 탐색하는 작업을 모든 node 수 만큼 반복하므로
O(N^2)의 시간 복잡도를 갖는다 (단, 최소힙 사용할 시 O(ElogN)로 개선 가능)
✅ 효율성 Tip
edge의 수가 적을 경우 O(ElogE)의 복잡도를 가지는 Kruskal's Algorithm,
edge의 수가 많을 경우 O(N^2)의 복잡도를 가지는 Prim's Algorithm이 효율적이다
이 문제의 경우
costs의 길이(edge의 수)는 ((n-1)*n)/2 이하 라는 조건이 주어졌기 때문에
결론적으로 Kruskal's Algorithm으로 구현하는 것이 보다 적합하다고 볼 수 있다
🔽 Kruskal's Algorithm 활용 코드 (C++)
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> parents;
bool cmp(const vector<int> &a, vector<int> &b) {
return a[2] < b[2];
}
int getParent(int x) {
if (parents[x] == x) { return x; }
return parents[x] = getParent(parents[x]);
}
void unionNodes(int x, int y) {
x = getParent(x);
y = getParent(y);
if (x < y) { parents[y] = x; }
else { parents[x] = y; }
}
// Solution #1 Kruskal's Algorithm 활용
int solution(int n, vector<vector<int>> costs) {
int answer = 0;
// 부모 노드 담는 벡터 초기화
for (int i=0; i<n; i++) { parents.push_back(i); }
// 건설 비용이 적은 순으로 정렬
sort(costs.begin(), costs.end(), cmp);
int size = costs.size();
for (int i=0; i<size; i++) {
int first = costs[i][0]; // 첫 번째 섬의 번호
int second = costs[i][1]; // 두 번째 섬의 번호
// 아직 통행이 불가능할 경우 (부모 노드가 다른 경우)
if (getParent(first) != getParent(second)) {
unionNodes(first, second); // 다리 건설
answer += costs[i][2]; // 비용 추가
}
}
return answer;
}🔽 Prim's Algorithm 활용 코드 (C++)
#include <string>
#include <vector>
#include <queue>
using namespace std;
struct Node {
int id; // 섬의 번호
int cost; // 비용
};
struct Cmp {
bool operator()(const Node &a, const Node &b) {
return a.cost > b.cost;
}
};
vector<bool> visited(100, false);
// Solution #2 Prim's Algorithm 활용
int solution(int n, vector<vector<int>> costs) {
int answer = 0;
priority_queue<Node, vector<Node>, Cmp> minHeap; // 비용이 적은 순으로 정렬되는 최소힙
minHeap.push({0, 0}); // 0번 섬을 기준으로 탐색 시작
int size = costs.size();
while (!minHeap.empty()) {
Node curNode = minHeap.top();
minHeap.pop();
if (visited[curNode.id]) {
// 이미 방문한 섬일 경우 스킵
continue;
}
visited[curNode.id] = true;
answer += curNode.cost;
for (int i=0; i<size; i++) {
// 인접한 섬들의 번호와 다리 건설 비용 minHeap에 push
if (costs[i][0] == curNode.id) {
minHeap.push({costs[i][1], costs[i][2]});
}
else if (costs[i][1] == curNode.id) {
minHeap.push({costs[i][0], costs[i][2]});
}
}
}
return answer;
}