[프로그래머스] 입국심사 (C++)

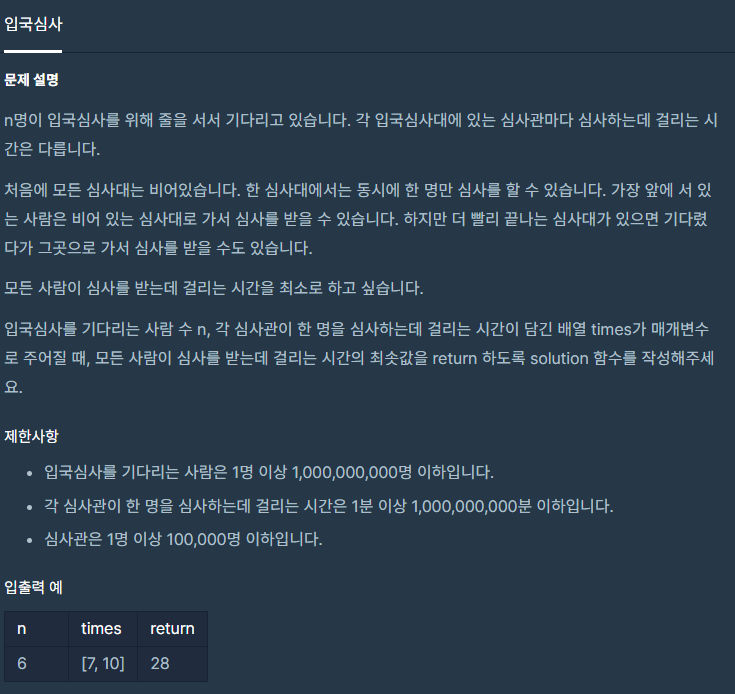
코딩테스트 고득점 Kit > 이분탐색

입국심사 | 문제 바로가기

문제풀이 (2022-02-27 SUN 💻)

🤔 사담

이분탐색.. 왜 이렇게 오랜만인 것 같지..
요즘 dfs/bfs랑 구현 문제만 주구장창 풀었더니 라는 비루한 변명은 저리가랏 💧
감도 안 잡혔다....

(times에 들어있는 가장 큰 값) * n 보다 작은
times에 들어 있는 수들의 배수들을 다 나열한 후
작은 순으로 n개를 뽑아서 더하면 되지 않을까.. 하는 일차원적인 생각밖에 안 났다..
오브콜스 시간 초과!
우리들의 착한 친구 구글링을 통해 깨달은 방법을 아래에서 살펴보도록 하자..

⭐ 풀이의 핵심

최솟값을 1, 최댓값을 times에 들어있는 가장 큰 값 * n 로 놓고
중간값을 구하여 해당 중간값 시점에 심사 완료 가능한 사람의 수를 구하여
문제에 주어진 n보다 크거나 같을 경우 answer를 해당 값으로 업데이트 해주는 방식으로
이분탐색을 계속 해나간다

🚨 실수 또는 간과한 부분

이 문제에서 또 중요한 것은
모든 변수를 int가 아닌 long long 으로 선언해줘야 한다는 것이다

특히 최댓값 (아래 코드에서 maxTime 변수) 을 초기화 할 때
times에 들어 있는 가장 큰 값 * n 값을 넣어주게 되는데
maxTime 변수를 long long으로 선언해주어도
times 벡터에 들어 있는 값도 int형, n도 int형 이므로,
int형 * int형을 해줄 때 이미 연산에서 오버플로우가 발생한다
따라서 적어도 둘 중 하나를 long long 으로 반드시 type casting 해주어야 한다!
ex) long long maxTime = times[times.size()-1] * (long long)n;

🔽 코드 (C++)

#include <string>
#include <vector>
#include <algorithm>
using namespace std;

long long completed(long long curTime, vector<int> times) {
    // curTime 시점에 심사 완료 가능한 사람 수를 return하는 함수
    long long cnt = 0;
    for (int i=0; i<times.size(); i++) {
        cnt += curTime / times[i];
    }
    return cnt;
}

long long solution(int n, vector<int> times) {
    long long answer = 0;
    
    sort(times.begin(), times.end()); // 오름차순 정렬
    long long minTime = 1; // 최소 시간
    long long maxTime = times[times.size()-1] * (long long)n; // 최대 시간
    
    // 이분탐색 활용
    long long midTime;
    while (minTime <= maxTime) {
        midTime = (minTime + maxTime) / 2;
        long long cnt = completed(midTime, times);
        if (cnt >= n) {
            answer = midTime;
            maxTime = midTime - 1;
        }
        else {
            minTime = midTime + 1;
        }
    }
    
    return answer;
}