[코딩테스트]백준 - 최소 스패닝 트리

최소 스패닝 트리

문제

그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.

최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.

입력

첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.

그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.

출력

첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.

예제 입력 1

3 3
1 2 1
2 3 2
1 3 3

예제 출력 1

3

출처

• 문제의 오타를 찾은 사람: BaaaaaaaaaaarkingDog
• 빠진 조건을 찾은 사람: tjrwodnjs999

해결한 나의 코드

function b1197(){
 var fs = require('fs');
 var input = fs.readFileSync('/dev/stdin').toString().split('\n');
 var info = input[0].split(' ').map(e => e / 1)
 var link = []
 for (var k = 1; k < input.length; k++) {
     link.push(input[k].split(' ').map(e => e / 1))
 }
 link = link.sort((a, b) => a[2] - b[2])
  
  var edge = []
  
  var cycleTable = new Array(info[0] + 1) // index 1 부터 사용하기 위해 +1 함
  for(var i=0; i<cycleTable.length; i++){
  	cycleTable[i] = i
  }
  
  var answer = 0
  var count = 0
  
  while(true){
  	var current = link[count] // 현재 정점 
    if(cycleTable[current[1]] !== cycleTable[current[0]]){ 
      // 만약 간선 연결 안되어있으면 
    	cycleTable = cycleTable.map(e => {
        if(e === cycleTable[current[1]]) return cycleTable[current[0]]
          // current[1]이랑 연결된 모든 애들에게 current[0]이랑도 연결되었다고 알려주기 
          else return e
        })
    }
    edge.push(current[2])
    // 간선 추가 
  }
  if(edge.length === info[0]-1){
    // 간선 갯수가 정점 갯수 - 1 이 되면 
  	break;
  }
  count++ // 다음 정점을 위해 count++
  
}
answer = edge.reduce((a,b) => a+b)
console.log(answer)

b1197()

알고리즘

최소 스패닝 트리(== 최소 신장 트리)를 구현하는 것.
따라서, 최소 스패닝 트리에 대한 개념을 알고 접근해야 한다.

1. 간선의 가중치에 따라 오름차순으로 정렬한다.
2. 사이클을 검사해주기 위한 cycleTable을 만든다.
   2-1. 연결하려는 두 정점의 cycleTable 값이 같다는 것 => 연결 하면 사이클 만들어진단 소리 !
   따라서 정점 연결할 때마다 cycleTable 값이 서로 같은지 다른지 확인해주어야 한다.
   사이클이 만들어지는 걸 피하기 위해 사용한다.
3. 이제 본격적으로 최소비용 신장 트리를 만든다 !!!
   ex. 예를 들면,

info = [3, 3]
link = [
  [1, 2, 1],
  [2, 3, 2],
  [1, 3, 3]
]

3-1. [1, 2, 1] 을 연결한다 ?
1의 연결상태 = 1 vs 2의 연결상태 = 2
서로 다르므로 연결 가능 -> edge에 push -> edge = [1]

3-2. [2, 3, 2] 를 연결한다 ?
2의 연결상태 = 1 vs 3의 연결상태 = 3
서로 다르므로 연결 가능 -> edge에 push -> edge = [1, 2]

3-3. info[0]-1 = 2 vs edge.length = 2 -> while 문 종료
3-4. 연결된 간선들의 합 == edge 원소들의 합 == 3

근데 테스트케이스가 너무 쉬운 것 같아서 내가 임의로 만든 테스트케이스로 다시 정리해보았다.

ex. 예를 들면,

info = [6, 8]
link = [
  [1, 2, 5],
  [1, 4, 2],
  [1, 5, 3],
  [2, 5, 1],
  [4, 5, 10],
  [2, 3, 2],
  [3, 6, 3],
  [5, 6, 4]
]

1. 가중치에 따라 오름차순으로 정렬한다.

link =  [
  [ 2, 5, 1 ],
  [ 1, 4, 2 ],
  [ 2, 3, 2 ],
  [ 1, 5, 3 ],
  [ 3, 6, 3 ],
  [ 5, 6, 4 ],
  [ 1, 2, 5 ],
  [ 4, 5, 10 ]
]

2. cycleTable도 만든다.

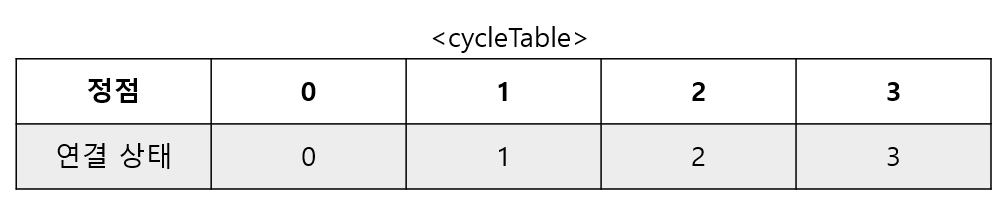
cycleTable:  [ 0, 1, 2, 3, 4, 5, 6 ]

3. current: [ 2, 5, 1 ] 이라면

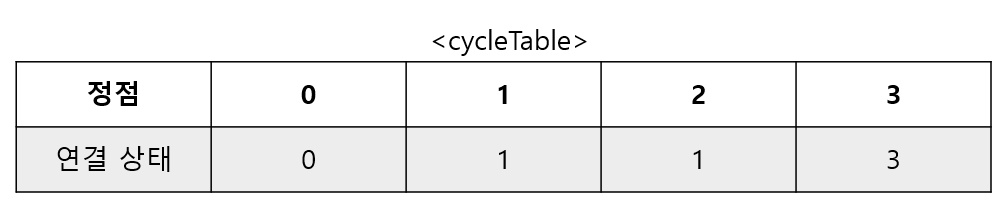
cycleTable:  [ 0, 1, 2, 3, 4, 2, 6 ]
edge:  [ 1 ]

2, 5는 사이클 상태가 서로 다르다 => 연결 가능하다 => 5의 연결상태는 2가 된다.

4. current: [ 1, 4, 2 ] 이라면

cycleTable:  [ 0, 1, 2, 3, 1, 2, 6 ]
edge:  [ 1, 2 ]

1, 4는 사이클 상태가 서로 다르다 => 연결 가능하다 => 4의 연결상태는 1이 된다.

5. current: [ 2, 3, 2 ] 이라면

cycleTable:  [ 0, 1, 2, 2, 1, 2, 6 ]
edge:  [ 1, 2, 2 ]

2, 3은 사이클 상태가 서로 다르다 => 연결 가능하다 => 3의 연결상태는 2가 된다.

6. current: [ 1, 5, 3 ] 이라면

cycleTable:  [ 0, 1, 1, 1, 1, 1, 6 ]
edge:  [ 1, 2, 2, 3 ]

5, 1은 사이클 상태가 서로 다르다 => 연결 가능하다 => 5의 상태는 1이 된다.
그런데 5는 2와 연결되어있었다 => 즉 2와 연결된 모든 정점들은 1과도 연결되게 된다.
따라서 연결상태가 2인 모든 정점의 연결상태를 1로 바꾼다.

7. current: [ 3, 6, 3 ] 이라면

cycleTable:  [ 0, 1, 1, 1, 1, 1, 1 ]
edge:  [ 1, 2, 2, 3, 3 ]

3, 6은 사이클 상태가 서로 다르다 => 연결 가능하다 => 6의 연결상태는 3의 연결상태인 1이 된다.

8. 연결된 간선의 갯수(edge.length)가 정점의 갯수-1이 되었다 => 최소 신장 트리 완성!

사실은 며칠동안 헤맸던 문제...
오타 하나 때문에 며칠을 헤맸었다... 풀고 나서 약간 허망했던 ㅜㅜ