🤖 등장 배경
단층 퍼셉트론을 여러층 쌓아올리면 어떨까? 하고 나오게 된 개념이 다층 퍼셉트론이다.
🤖 개념
앞서 배운 퍼셉트론은 단층 퍼셉트론이다. 다층 퍼셉트론은?
단층 퍼셉트론을 여러개 쌓은 것이다.
하나 이상의 은닉층(Hidden Layer)을 가진 퍼셉트론.
MLP (Multi-Layer Perceptron) 라 한다.
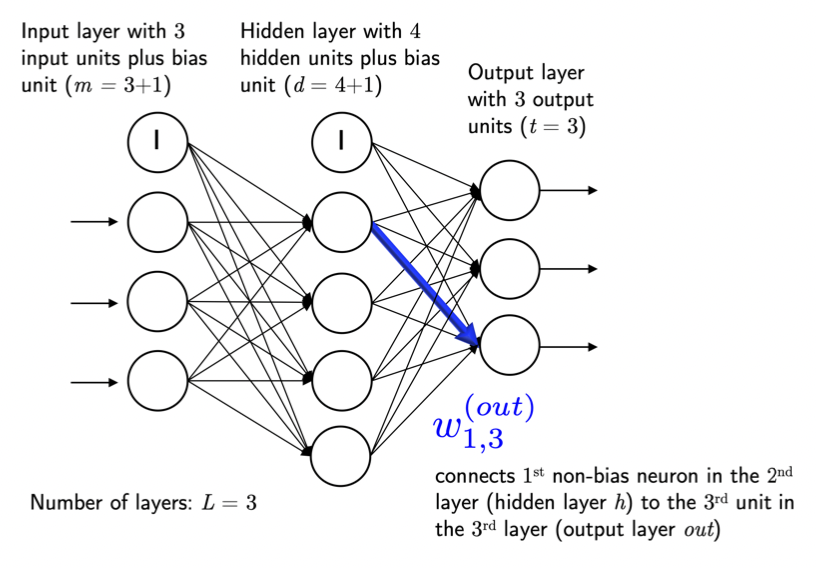
🤖 학습 과정
인공 신경망의 학습은 오차(예측값과 실제값 차)를 최소화하는 "가중치"를 찾는 목적으로 순전파와 역전파를 반복한다.
🔺 Forward Pass (순전파)
(입력층 → 출력층) 의 방향으로 계산.
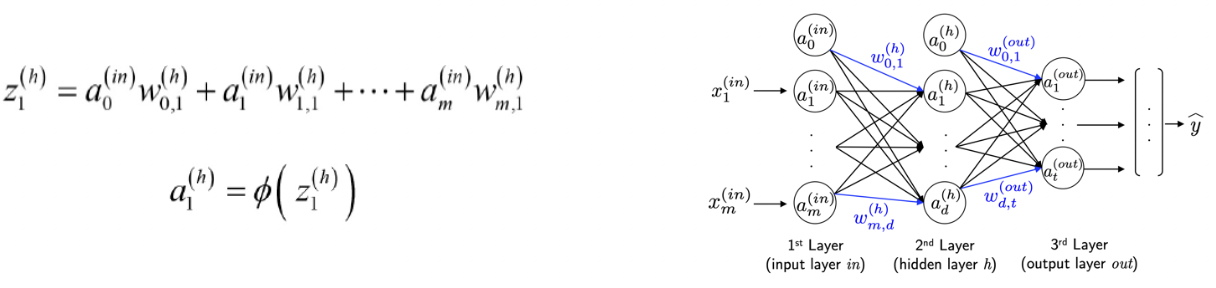
-
입력(a)과 그에 해당하는 가중치(w)를 곱한 값들의 합을 활성화 함수(activation function)에 전달한다.
-
활성화 함수로 부터 리턴된 값을 다시 input으로 보고, 위 과정을 반복하여 출력층까지 차례대로 계산한다.
-
최종 활성화 함수에서 출력값(^y)이 계산되고, 이 출력값(^y)와 실제값(y)를 손실함수에 넣어 연산하여 오차(cost)를 계산한다.
이제, 순전파 과정을 통해 나온 오차(cost)를 활용해 각 층의 가중치(w)와 편향(bias)를 최적화 해야한다.
오차의 최솟값을 구하기 위해 '경사하강법'을 이용해 각 층의 오차의 미분값을 구해서 가중치(w)와 편향(bias)를 업데이트를 한다.
그런데 여기서 문제점이 발생한다 !!!
MLP 층의 수가 많아지면서 미분을 통해 신경망을 업데이트하려면 순전파를 몇번이고 다시 수행해야한다.
그러면 연상량이 많아지므로 굉장히 비효율적이게 된다.
-> 그래서, Back propagtion 알고리즘으로 이를 해결한다.
🔻 Backpropagation (역전파)
(출력층 → 입력층) 의 방향으로 계산.
입력값과 출력값을 알고 있는 상태에서 신경망을 학습 시키는 방법이다. Supervised learning(지도학습)이라고 한다.
역전파 과정에서는 각각의 가중치와 편향을 최적화하기 위해 "연쇄 법칙(Chain Rule)"을 활용한다.
새로 계산된 가중치는 "최적화(Optimization) 알고리즘"을 통해 오차를 최소로 줄일 수 있는 가중치와 편향을 계산한다.
따라서 순전파를 통해 오차를 계산했다면, 역전파를 통해서는 반대방향으로 중간 변수와 파라미터에 대한 미분값을 계산하고 저장해서 오찻값이 0이 될 수 있도록 가중치를 갱신한다.
🤖 이후의 문제점 ...
1. Overfitting
트레이닝 셋에 너무 과최적화되어 실제 데이터를 집어 넣어 분류를 하려고 하면 정확도가 좀 떨어지는 것
2. Vanishing Gradient
층을 거치면서 계속 경사하강법을 통해 미분하고 미분하고 하다보니, 뒤로 전해지면서 에러값이 현저히 작아져 학습이 제대로 안되는 것
