🤖 등장 배경

McCulloch-Pitts 뉴런 모델의 등장

1943년 'McCulloch-Pitts Neuron Model' 이 제시됨.

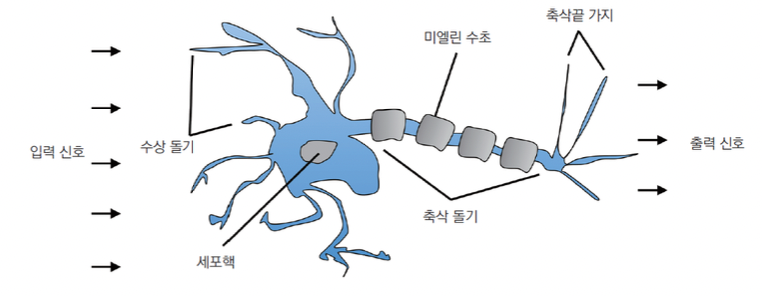
• 최초의 간소화된 뇌의 뉴런 개념.
• 출력이 Binary인 간단한 모델.
• 수상 돌기에 도착한 여러 신호가 세포체에 합쳐짐.
• 합쳐진 신호가 특정 값을 넘으면 축삭 돌기를 이용하여 출력 신호가 전달됨.

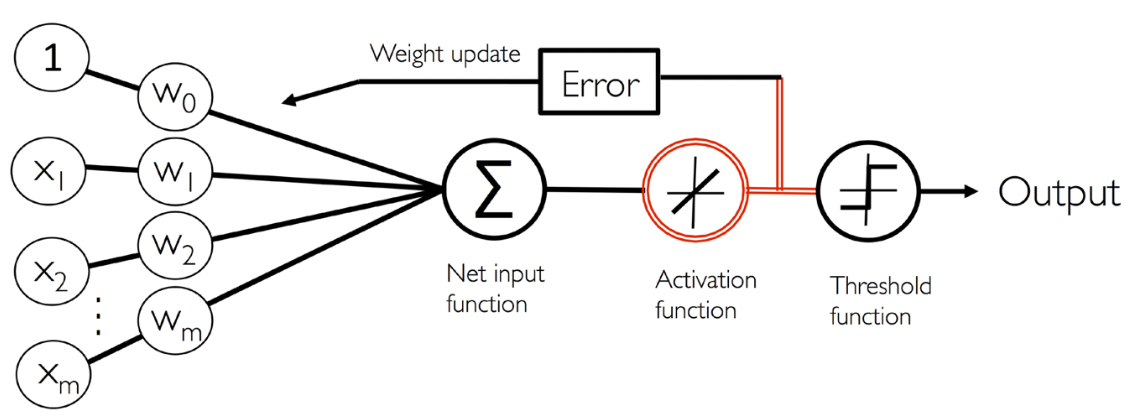
이후, 위의 동작 과정을 모델링한 알고리즘인 퍼셉트론이 등장함.

🤖 개념

퍼셉트론은 위의 동작 과정(생물학적인 신경계의 기본 단위인 뉴런의 동작 과정)을 통계학적으로 모델링한 알고리즘이다.

🤖 특징

이진 분류

'뉴런 모델'의 출력이 Binary 한 것 처럼 '퍼셉트론'도 이진뷴류(Binary Classification)에 적용가능하다.

• Positive Class : +1
• Negative Class : -1

Step Function (계단 함수)

-> 임계값 넘으면 P, 넘지 못하면 N

결정 함수는 입력 벡터 x와 가중치 w의 선형 조합이다. 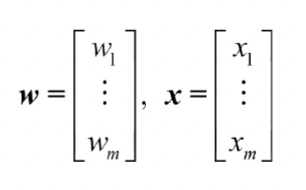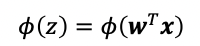z 값 >= Threshold ➡️ Positive
z 값 < Threshold ➡️ Negative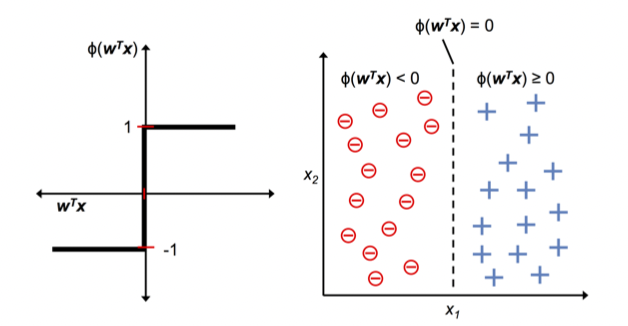

🤖 학습 과정

학습 규칙

• x(입력값), y(출력값), w(가중치)

1. 가중치 w를 0 또는 작은 값으로 랜덤 초기화.
2. 각 샘플 x에 대한 출력값 ˆy 계산.
3. 예측이 정확한 경우(y와 ^y이 같은 경우)는 가중치를 그대로 유지하고,
   예측이 틀린 경우(y와 ^y가 다른 경우)는 가중치를 업데이트.
4. 가중치 유지 or 업데이트 후 수렴까지 반복.

학습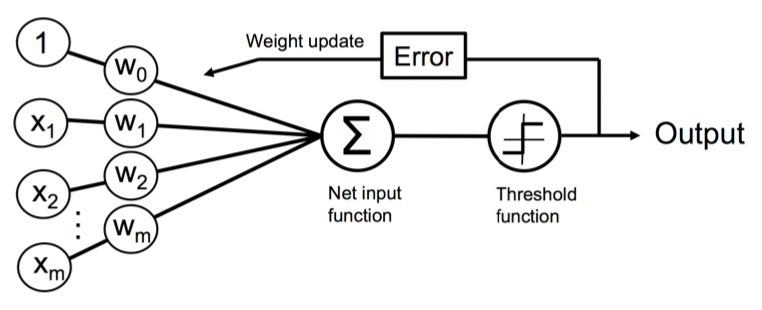

선형적으로 구분 가능한 데이터에 대해 사용한다. ( 데이터가 선형 구분 가능하지 않으면 update가 멈추지 않는다. )
학습률이 충분히 작을 경우 수렴이 보장된다.

🤖 이후...

'ADALINE'의 등장

퍼셉트론 등장 몇 년 후 Adaptive Linear Neuron (ADALINE) 등장.

• 가중치 업데이트를 위해 Step Function 이 아닌 Linear Activation Function을 사용 !!
  -> 뉴런에서 출력값을 변경시키는 함수
• Class Label과 실수 출력 값을 비교하여 오차를 계산 (미분 가능한 비용 함수, Gradient Descent 이용 가능)