
본 < 지능형 시스템 > 시리즈는 부산대 정보컴퓨터공학과 차의영 교수님의 '지능형 시스템' 강의에서 배운 내용을 바탕으로 작성합니다.
🕹 퍼지 이론이란?
우리의 일상은 애매모함으로 넘친다. 불완전하고, 부정확한 자료를 처리하기 위해 신경회로망을 사용하는 것인데, 여기에 퍼지 이론(fuzzy logic)을 추가하면 또 다른 애매모한 처리의 상승효과가 가능하다.
- 퍼지 이론과 확률 이론의 닮은 점
✔️ 퍼지 멤버십(fuzzy membership) 과 확률의 값은 0-1 사이이다.
✔️ 확률의 1은 어떤 사건이 일어날 확실성을 나타내고,
✔️ 애매모호함(fuzziness)의 1은 특정 집합에 속하는 대상에 관한 확실성을 나타낸다.
- union, intersection, complement
✔️ A와 B의 union = 두 개중 더 큰 것.
✔️ A와 B의 intersection = 두 개중 더 작은 것.
✔️ A의 complement = 1 - A
📌 예시)
A = [ 0, 0.3, 0.7, 0.4, 0.8], B = [0.8, 0.2, 0.6, 0.7, 0.9]
A ∪ B = [0.8, 0.3, 0.7, 0.7, 0.9]
A ∩ B = [0, 0.2, 0.6, 0.4, 0.8]
A'= [1, 0.7, 0.3, 0.6, 0.2]
A ∪ A' = [1, 0.7, 0.7, 0.6, 0.8]
A ∩ A' = [0, 0.3, 0.3, 0.4, 0.2] -> 확률과는 다르게 0이 아니다 !!!
- cardinality, subset
✔️ cardinality = 퍼지벡터의 크기로 '요소들의 합'이다. M 으로 표현.
✔️ A가 B의 부분집합인 정도 = S(A,B) = M(A∩B)/M(A)
📌 예시)
M(A) = 2.2, M(B) = 3.2
M(A∩B) = 2.0
S(A,B) = 2.0/2.2 = 0.909
S(B,A) = 2.0/3.2 = 0.625
- Crisp VS Fuzzy
✔️ Crisp는 0과 1만 다루지만, Fuzzy는 0부터 1사이 값을 다룬다.
✔️ arithmetic operations ⭐️⭐️⭐️ -> 중앙 값 계산 후, 각 구간의 평균을 구하여 앞 뒤로 +- 해준다.
📌 예시)
a = [-2, 3, 8] -> 구간: 10
b = [-1, 2, 7] -> 구간: 8 , 따라서 구간의 평균은 (10+8)/2 = 9
a+b = [-4, 5, 14]
a-b = [-8, 1, 10]
axb = [-3, 6, 15]
a/b = [-7.5, 1.5, 10.5]
🕹 Hybrid Learning System
🎨 전체적인 그림
✔️ 기존의 역전파 문제점: 적절한 학습률을 선택하기 어렵다.
✔️ 해결책: 퍼지이론을 추가한 하이브리드 학습 시스템을 이용한다.
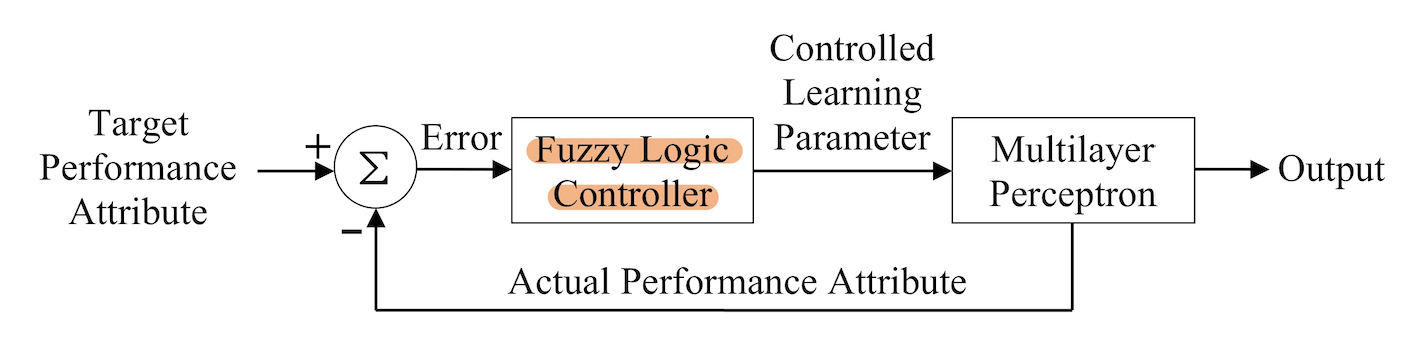
아래 그림은 하이브리드 학습 시스템이다.
학습률 계수를 잘 조절하여 수렴을 더 잘할 수 있게 해주는 시스템이다.
🎨 Fuzzy Logic Controller
Fuzzy logic controller는 역전파 학습을 하는 다층 퍼셉트론의 학습률 계수를 알맞게 하기 위해 사용된다. 그렇기에 수렴율 개선에 도움이 된다.
이때, 역전파의 학습률 계수의 인간언어적 서술을 돕는다.
예를들어, 역전파가 수렴하지 않을 때 "학습률을 조금 낮춰봐라"라고 말할 수 있는데, 여기서 '조금'이라는 말 자체가 퍼지한 말이다. 그래서 이를 처리하기 위해 퍼지 이론을 적용한다.
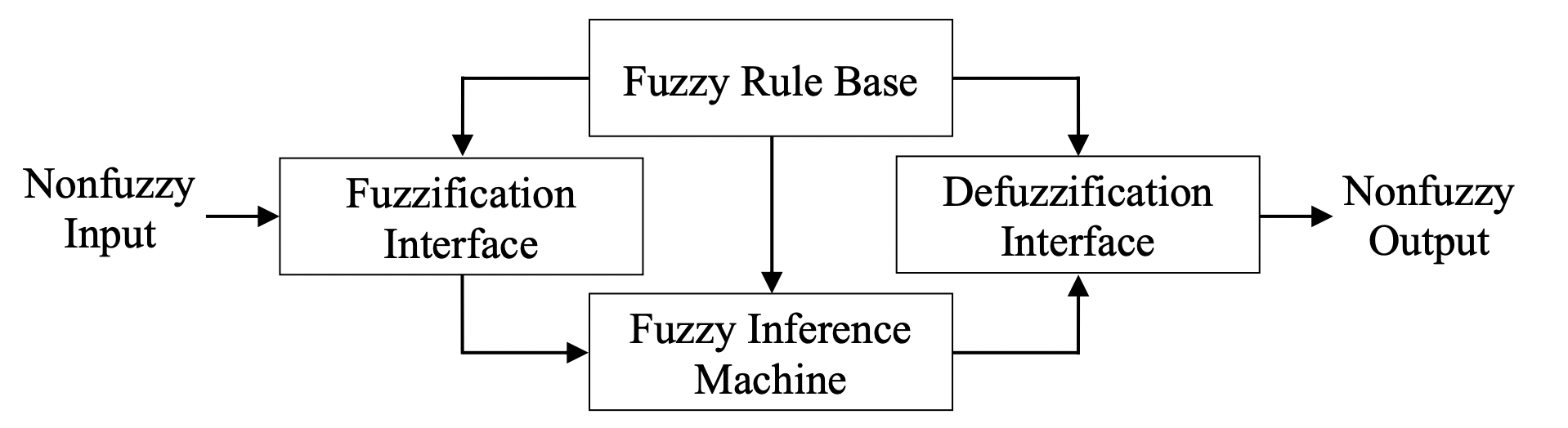
(1) Fuzzification Interface
- 입력변수 값(=crisp한 값)의 범위에 일치하는 universe of discourse로 변화시키는 scale mapping 이다.
- 입력변수 값(=crisp한 값)을 적절한 언어적 값으로 바꾸는 fuzzification 이다. 즉, fuzzified input을 만드는 과정이다.
- ex ) 32.5 에러값이 입력 데이터로 들어오면 '큰 값'이라는 적절한 언어적 값으로 바꿔준다.
(2) Fuzzy rule base
- IF-THEN 형태로 쓰여진 언어적 제어 규칙의 집합이다.
- ex ) If 에러가 '큰 값'이면, then 학습률 계수를 낮춰라.
(3) Fuzzy inference machine
- fuzzified 된 입력값에 대응하여 fuzzy control action을 추론하기 위한 fuzzy rule base 로 부터 규칙을 채택하는 의사 결정 논리(decision-making logic)이다.
- ex ) 에러값이 '큰 값'이라는 fuzzified input과 IF-TEHN 규칙으로부터 학습률 계수를 낮추는 규칙(fuzzy control action)을 채택한다.
(4) Defuzzicaion interface
- 출력변수 값의 범위에 일치하는 universe of discourse로 변화시키는 scale mapping 이다.
- 추론된 fuzzy control action으로 부터 nonfuzzy(crisp) control action을 내는 defuzzification 이다. 즉, crisp output을 만드는 과정이다.
- ex ) 학습률 계수를 낮춘다 -> 학습률 계수를 '0.05'로 줄여라.
여기서, fuzzy control의 핵심은 수렴 속도를 빠르게 하기 위해 fuzzy IF-THEN-rule의 형태로 heuristic을 구현하는 것이다. 여기서 Heruistic은 sum of squared error E에 의해 조정된다.
🎨 Heuristic
CE(change of error)
- Error surface의 미분값의 근사치이다.
- 그렇기에 Error surface의 미분값의 부호 변화는 CE의 부호 변화와 동일하다.
CCE(change of CE)
- 수렴의 가속도와 관련된 second-order 미분값의 근사치이다.
- CCE는 CE 두개의 차이값이다.
Rule base
- CE 값이 계속 + 이거나 계속 - 라면, 학습률 계수가 작다고 판단하여 학습률 계수를 증가시키고자 한다.
- Error가 계속 진동되고 있으면, 학습률 계수가 크다고 판단하여 학습률 계수를 감소시키고자 한다.
- 대체로 CE가 계속 - 이면 CCE는 + 이고, CE가 계속 + 이면 CCE는 - 인 경향이 있다.
예시
E(n-2) = 0.34, E(n-1) = 0.32, E(n) = 0.33- n-1과 n-2 사이 CE 값: 0.32 - 0.34 = -0.02
- n과 n-1 사이 CE 값: 0.33 - 0.32 = 0.01
- CCE 값: 0.01 - (-0.02) = 0.03
Fuzzy 관련 이론
퍼지이론을 이용한 컨테이너 트레일러ㆍ트럭의 주차제어, 1999년, pp.1 - 9 , 박계각
