Game Theory 에서 MINIMAX algorithm을 사용할 경우 너무 많은 노드가 생성될 수 있다. 이런 경우 연산 시간과 메모리 문제가 발생할 우려가 있고, 실제 문제에 적용하기 곤란하여 노드의 절단이 필요하게 된다.
이때 사용하는 것이 Alpha-Beta Pruning algorithm이다.
📎Alpha-Beta Pruning
https://commons.wikimedia.org/w/index.php?curid=3708424
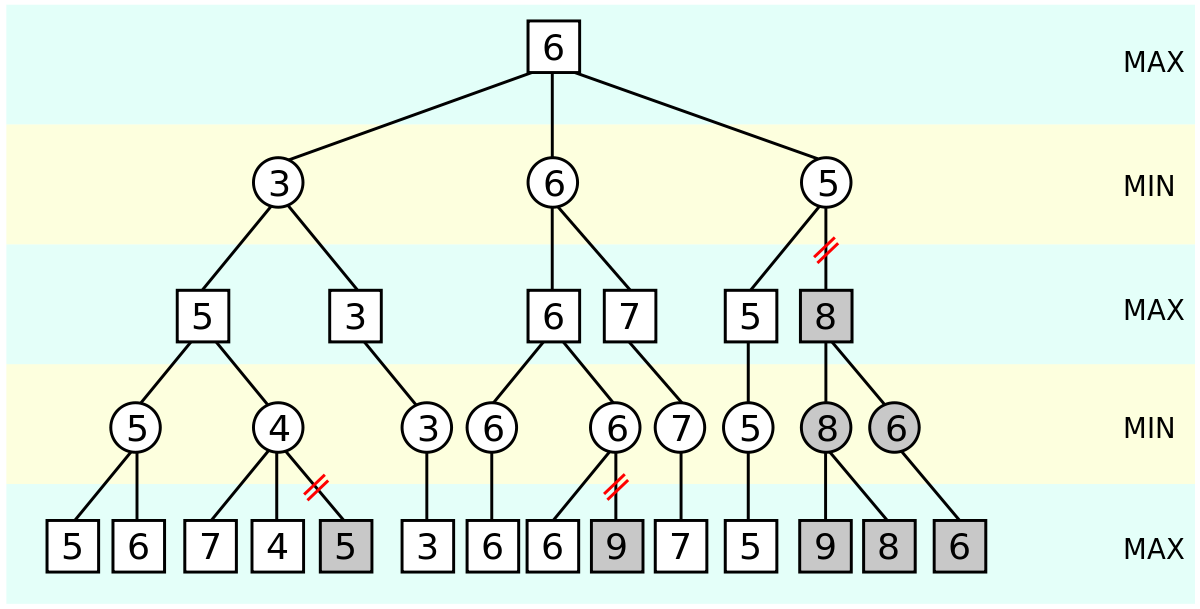
기본 베이스는 MINIMAX 알고리즘에 기반한다.
MAX 로 표시된 층에서는 큰 수를 선택하는 것이 좋고(나의 이익이 최대가 되는 선택), MIN으로 표시된 층에서는 작은 수(게임 상대의 입장에서 나의 이익이 최소가 되는 선택)가 선택 된다.
여기서 기억해야 할 부분은
Alpha-Beta Pruning은 가지치기를 함으로써 다음 노드를 아예 탐색의 고려조차 하지 않고 넘어간다는 것이다.
Alpha-Beta Pruning의 정확한 solution으로는 a와 b값을 따로 구분하여 설정해야한다.
(참고 : https://merry-nightmare.tistory.com/173)이 풀이는 시험을 위해 빠르게 해결하기 위해 자체적으로 해석한 풀이입니다. alpha-cutoff, beta-cutoff를 사용하는 기존의 풀이는 위의 주소를 참고해주세요.
다만 이 문제를 간단하게 풀기 위해 부등식을 활용하고자 한다.
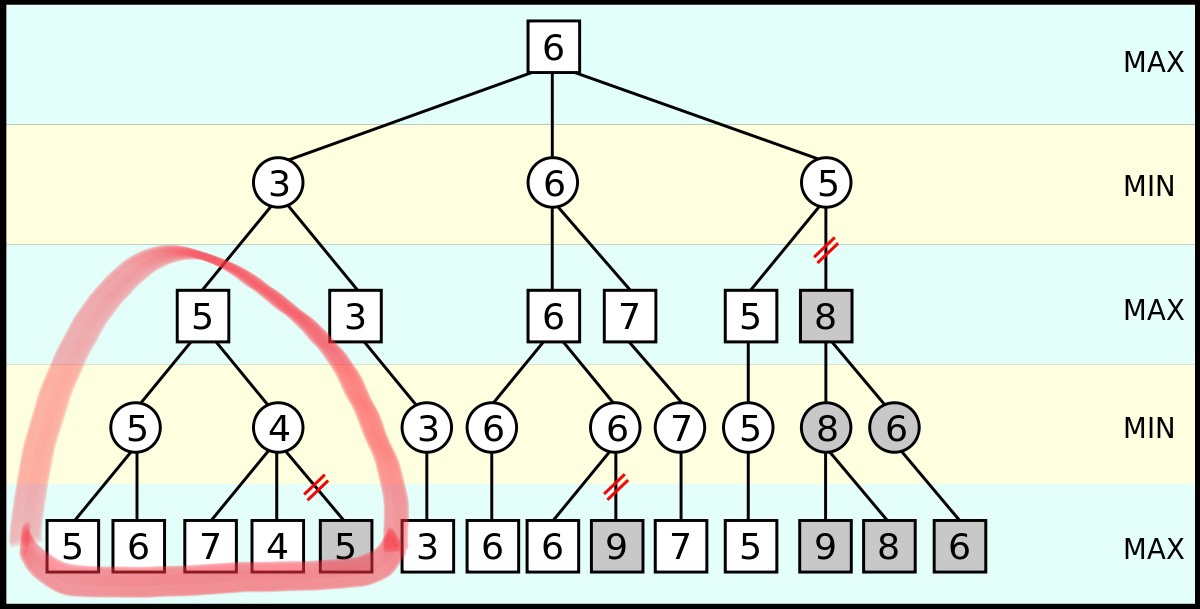
빨간 색으로 표시된 부분만 살펴보자.
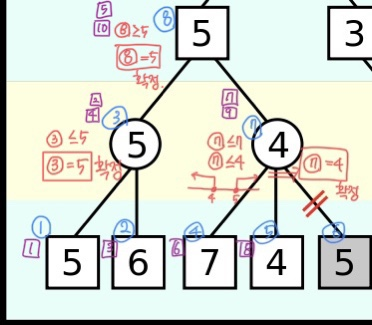
파란색 동그라미로 표시한 숫자는 설명의 편의를 위해 임의로 정한 노드의 이름 대신 부를 숫자이다.
(맨 왼쪽 아래의 5 노드가 1번 노드이다.)보라색 네모로 표시한 숫자는 탐색되는 순서이다.MIN층에서는 아래의 층에서 작은 수를 골라야 하고,MAX층에서는 아래 층에서 큰 수를 골라야 한다.
빨간 색으로 표시된 메모에 집중해서 봐야한다.
-
1번 노드를 탐색한 후 3번 노드에는 일단 숫자 5가 들어간다. (아무것도 탐색된게 없기 때문이다.
-
이때 3번 노드에 5보다 작은 수가 들어가면 3번 노드의 값은 바뀐다.(
MIN층이기 때문이다.)③<=5
-
2번 노드를 탐색하니 2번 노드의 수가 6이기 때문에 3번 노드의 값은 바뀌지 않고 5로 확정된다.
③=5 확정
-
3번 노드에서 확정된 숫자 5는 8번 노드로 올라간다.
-
이때 8번 노드에 5보다 큰 수가 들어가면 8번 노드의 값은 바뀐다.(
MAX층이기 때문이다.)⑧>=5
-
이후에 4번 노드로 내려가서 탐색한다.
-
4번 노드를 탐색하니 숫자 7이 있으니 일단 7번 노드에 숫자 7을 넣는다.
-
이때 7번 노드에 7보다 작은 수가 들어가면 7번 노드의 값은 바뀐다.
(MIN층이기 때문이다.)⑦<=7
-
5번 노드를 탐색하니 7보다 작은 4가 들어있다.
-
그러므로 7번 노드의 수를 4로 바꾼다. ( 7번 노드에 4보다 작은 수가 들어가면 4번 노드의 값은 바뀐다.)
⑦<=4
-
이때 6번 노드는 탐색하지 않고 7번 노드는 4로 확정, 8번 노드는 5로 확정하고 탐색을 종료한다.
- 7번 노드에는 이미 5보다 작은 값이 들어있다.
- 6번 노드를 탐색해 7번 노드에 4보다 작은 어떤 값이 들어가더라도 8번 노드의 결과와 더 상위 노드의 결과에는 영향을 주지 않는다. ( 부등식의 해가 존재하지 않기 때문이다.)
- 그러므로 6번 노드의 값을 탐색조차 하지 않고 가지를 치고 각각의 노드 값을 확정한다.
⑦ = 4 , ⑧ = 5 확정
이 과정을 반복하면 원래의 이미지와 같은 가지치기된 트리 형태가 된다.
참고 :
https://going-to-end.tistory.com/entry/%EC%95%8C%ED%8C%8C-%EB%B2%A0%ED%83%80-%EA%B0%80%EC%A7%80%EC%B9%98%EA%B8%B0-Alpha-beta-pruning
https://merry-nightmare.tistory.com/173
