[Algorithm] Big-O 표기법

📎시간 복잡도

알고리즘의 효율성에 대해 수행시간으로 나타낼 때 시간복잡도를 사용한다.
시간 복잡도는 알고리즘이 실행되는 동안에 사용된 기본적인 연산 횟수를 입력 크기의 함수로 나타낸다.

📎Big-O 표기 , O-표기

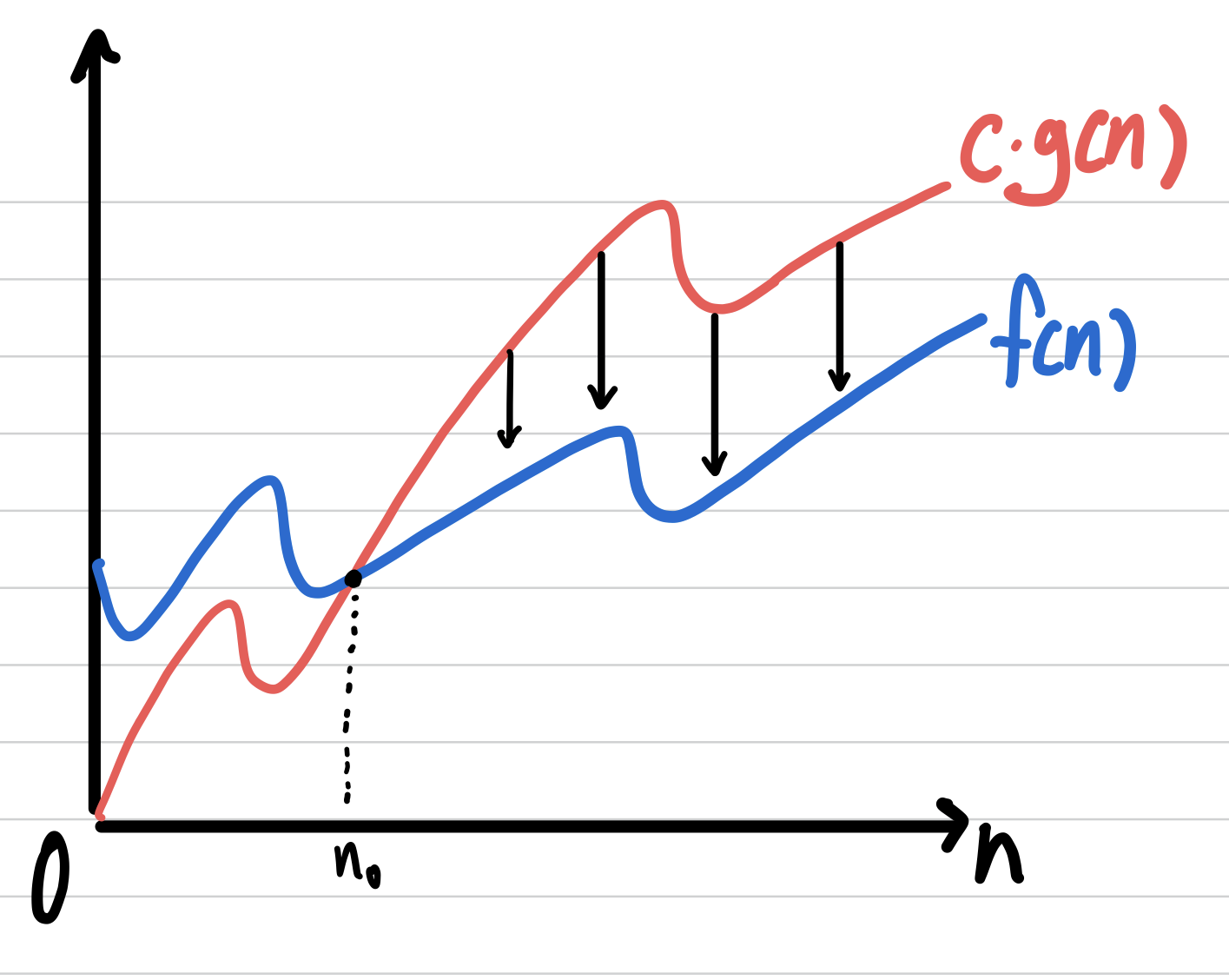
모든 n>=n0에 대해 f(n)<=g(n)이 성립하는 양의 상수 c와 n0가 존재하면, f(n)=O(g(n))이다.
이때, g(n) = f(n)의 상한(upperbound)이다.

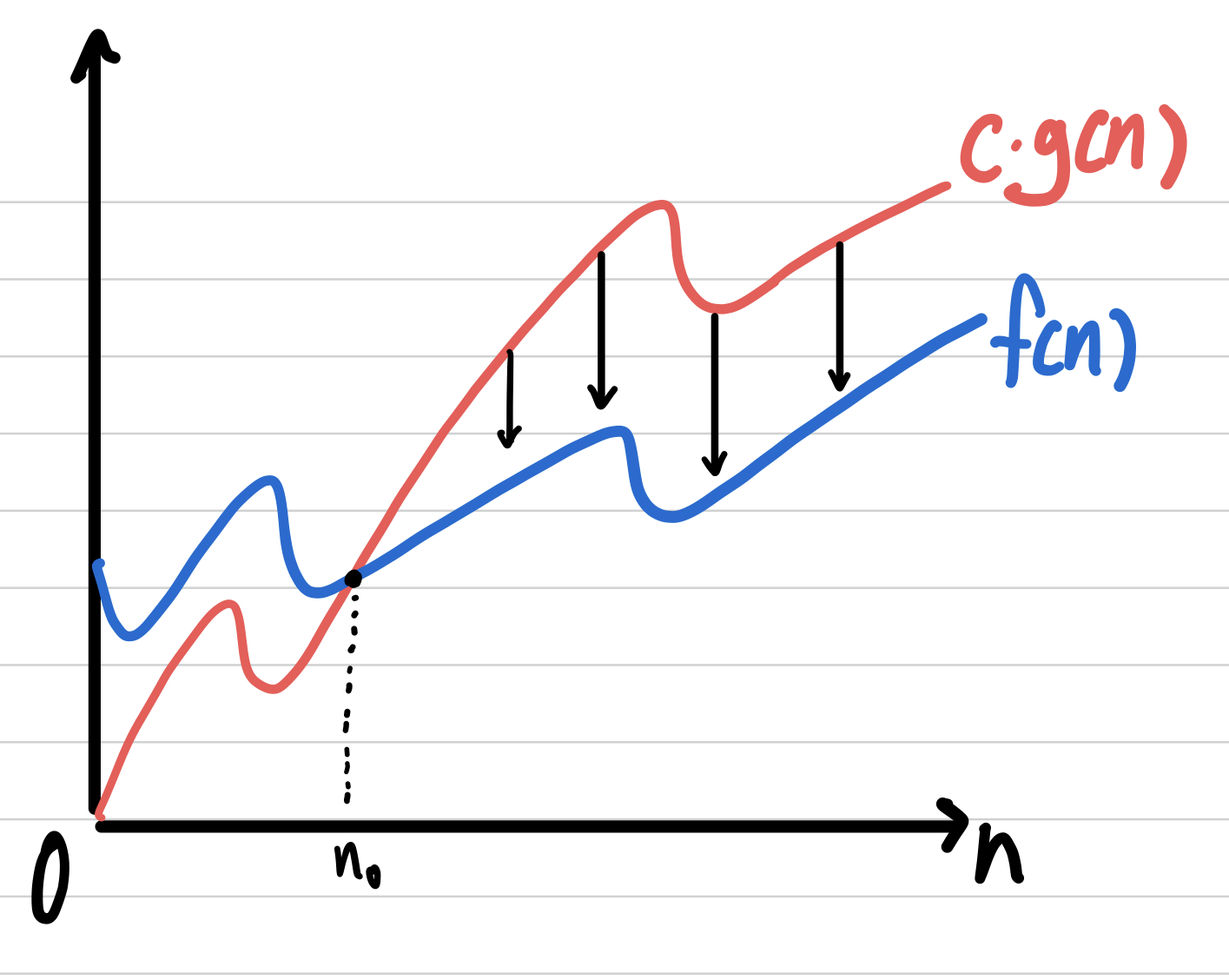
입력크기 n이 커질수록 수행시간 차이가 커지기 때문에 n이 커지는 경우에 O-표기가 효과적이다.

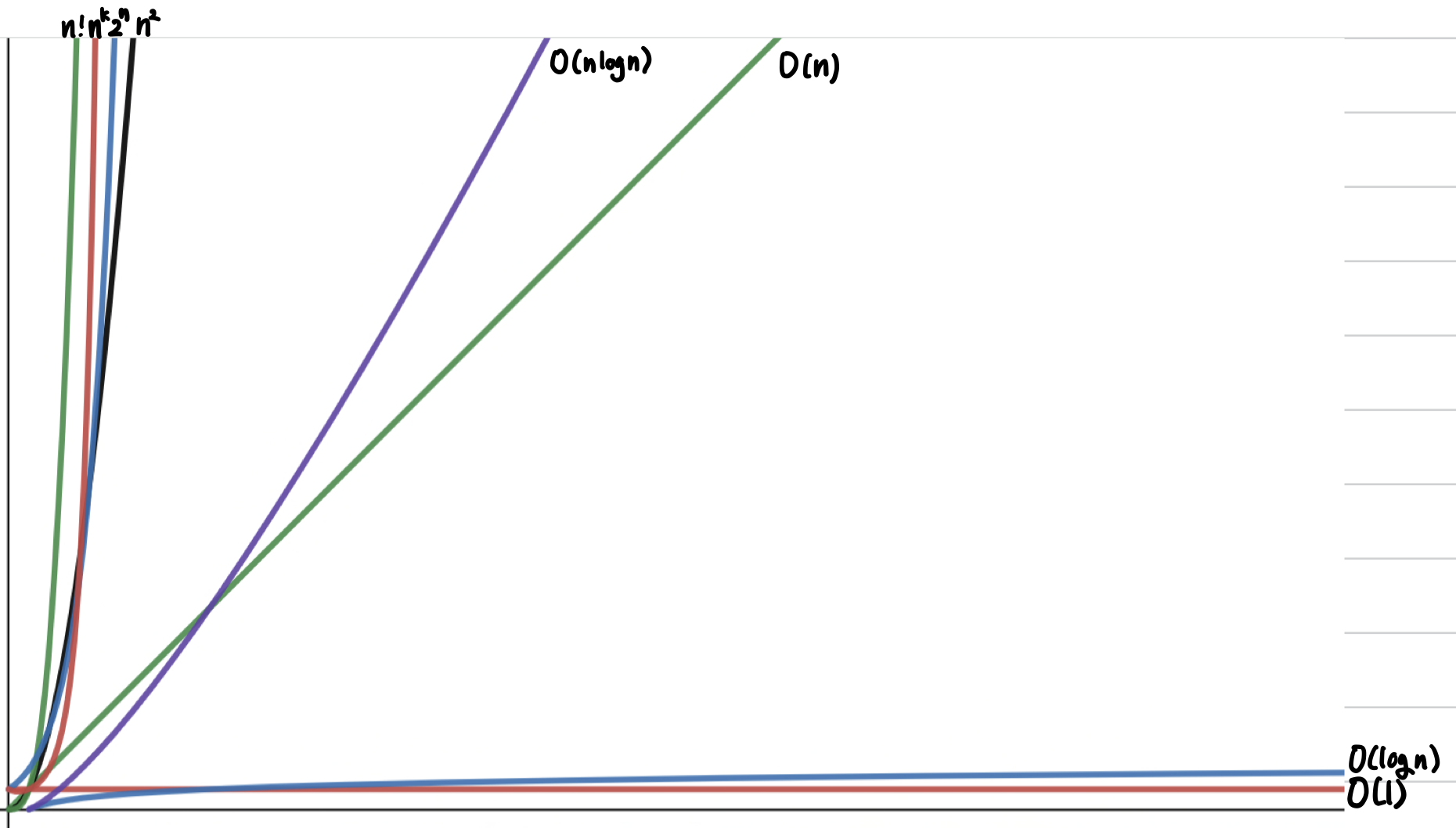
위의 그래프와 같이 시간복잡도는 다음과 같은 포함 관계이다.
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^k)<O(2^n)<O(n!)

기본적으로 시간복잡도는 알고리즘의 연산 횟수를 점화식으로 나타내 구할 수 있다.

---

📎O(1)

: 입력된 데이터에 상관 없이 언제나 일정한 시간이 걸린다.
Ex)

F(int[] n){
	return (n[0]==0)? true: flase;
}

---

📎O(n)

: 입력 데이터의 크기에 비례해서 처리속도가 증가한다.
Ex)

F(int[] n ){
	for i = 0 to n.length
    	print i
}

---

📎O(n^2)

: 입력 데이터의 크기의 제곱만큼 연산을 수행한다. (n번을 n회 수행한다.)
Ex)

F(int[] n){
	for i = 0 to n.length
    	for j = 0 to n.length
        	print i + j;
}

---

📎O(mn)

✏️ 변수가 다르다면 반드시 다르게 표기한다.
Ex)

F(int[] n , int[] m ){
	for i=0 to n.length
    	for j = 0 to m.length
        	print i+j;
}

---

📎O(n^3)

: 입력 데이터의 세제곱만큼 연산을 수행한다.
Ex)

F(int[] n){
	for i=0 to n.length
    	for j=0 to n.length
        	for k=0 to n.length
            	print i + j + k;
}

---

📎O(2^n)

:연산의 수행 횟수가 2개씩 n번 증가한다 (피보나치 수열의 기본 형태)

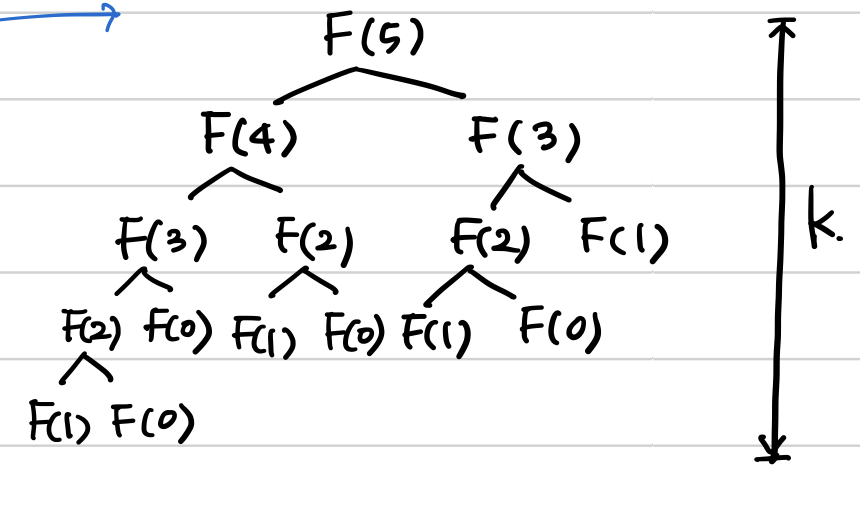
Ex)

F(n,r){
	if(n<=0) return 0;
    else if ( n==1) return r[n]=1;
    return r[n]=F(n-1,r)+F(n-2,r);
}

cf) O(m^n) : m개씩 n번 증가

---

📎O(log n)

:실행마다 처리할 데이터가 절반 씩 감소
ex) binary search : 중간 값 기준으로 한 쪽 부분 필요 x (절반 감소)
Ex)

F(k,arr,s,e){
	if(s>e) return -1;
    m = (s+e)/2;
    if(arr[m]==k) return m;
    else if (arr[m]>k) return F(k,arr,s,m-1);
    else return F(k,arr,m+1,e);
}

참고 :
https://youtu.be/6Iq5iMCVsXA