💻Divide & Conquer Algorithm
- 주어진 문제의 입력을 분할하여 문제를 해결(정복)하는 방식의 알고리즘
- 분할한 입력에 대하여 동일한 알고리즘을 적용하여 해를 계산
- 이들의 해를 취합해 원래 문제의 해를 얻음.
- 부분 문제와 부분 해
- 분할된 입력에 대한 문제 = 부분 문제(subproblem)
- 부분 문제의 해 = 부분 해
- 부분 문제는 더 이상 분할할 수 없을 때까지 분할
📎분할 과정
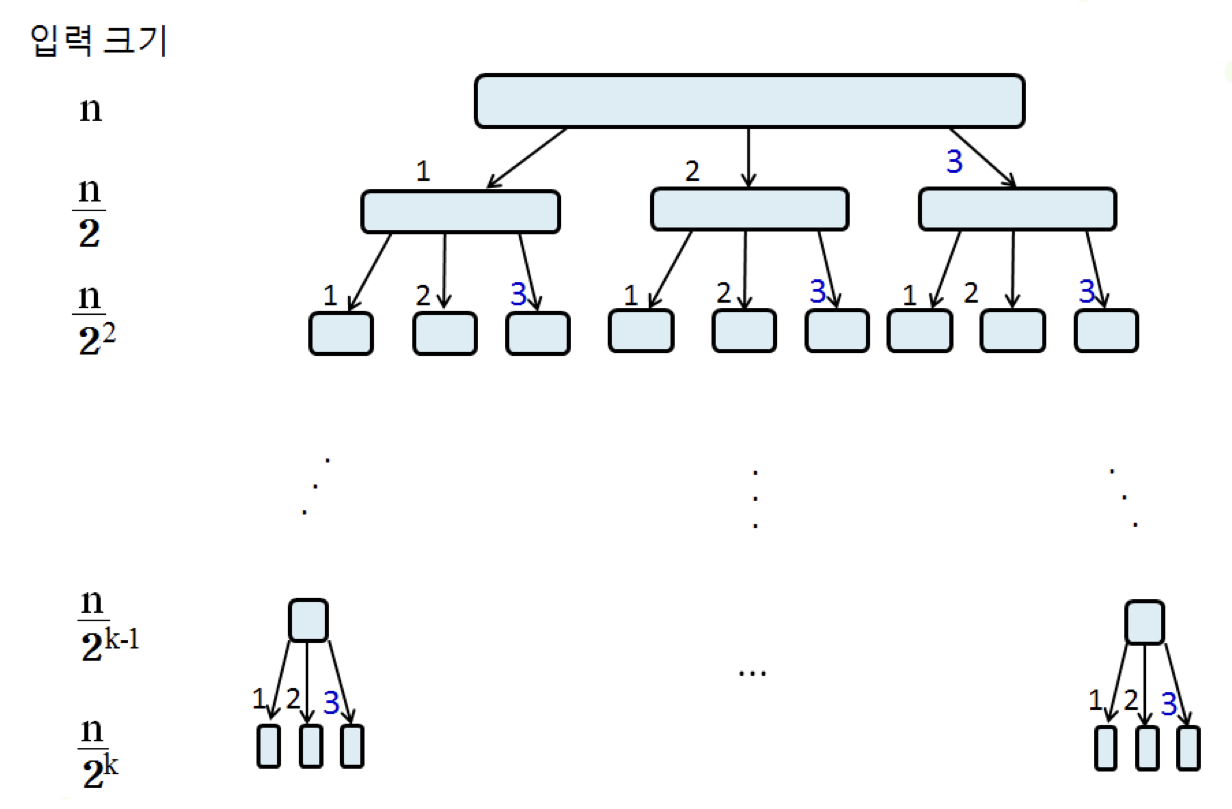
🔼입력 크기가 n인 문제를 3개로 분할하고, 각각 분할된 부분 문제의 크기가 n/2일 경우의 분할.
- n/2^k = 1 일 때 분할을 중단한다.
- k = log2n
- 전체 문제의 복잡도 : log2n * O(n)
📎1. Merge Sort
: 입력이 2개의 부분 문제로 분할되고, 부분 문제의 크기가 1/2로 감소하는 알고리즘.
- n개의 숫자들을 n/2개씩 2개의 부분 문제로 분할
- 각각의 부분 문제를 순환으로 합병 정렬
- 2개의 정렬된 부분을 합병하여 정렬(정복)
✏️psuedo code
MergeSort(A,p,q)
//입력 : A[p]~A[q]
//출력 : 정렬된 A[p]~A[q]
1. if(p<q){ //배열의 원소의 수가 2개 이상이면
2. k=(p+q)/2 //k는 중간 원소의 인덱스
3. MergeSort(A,p,k) //앞부분 순환호출
4. MergeSort(A,k+1,q) //뒷부분 순환호출
5. A[p]~A[k]와 A[k+1]~A[q]를 합병
}✏️수행 과정
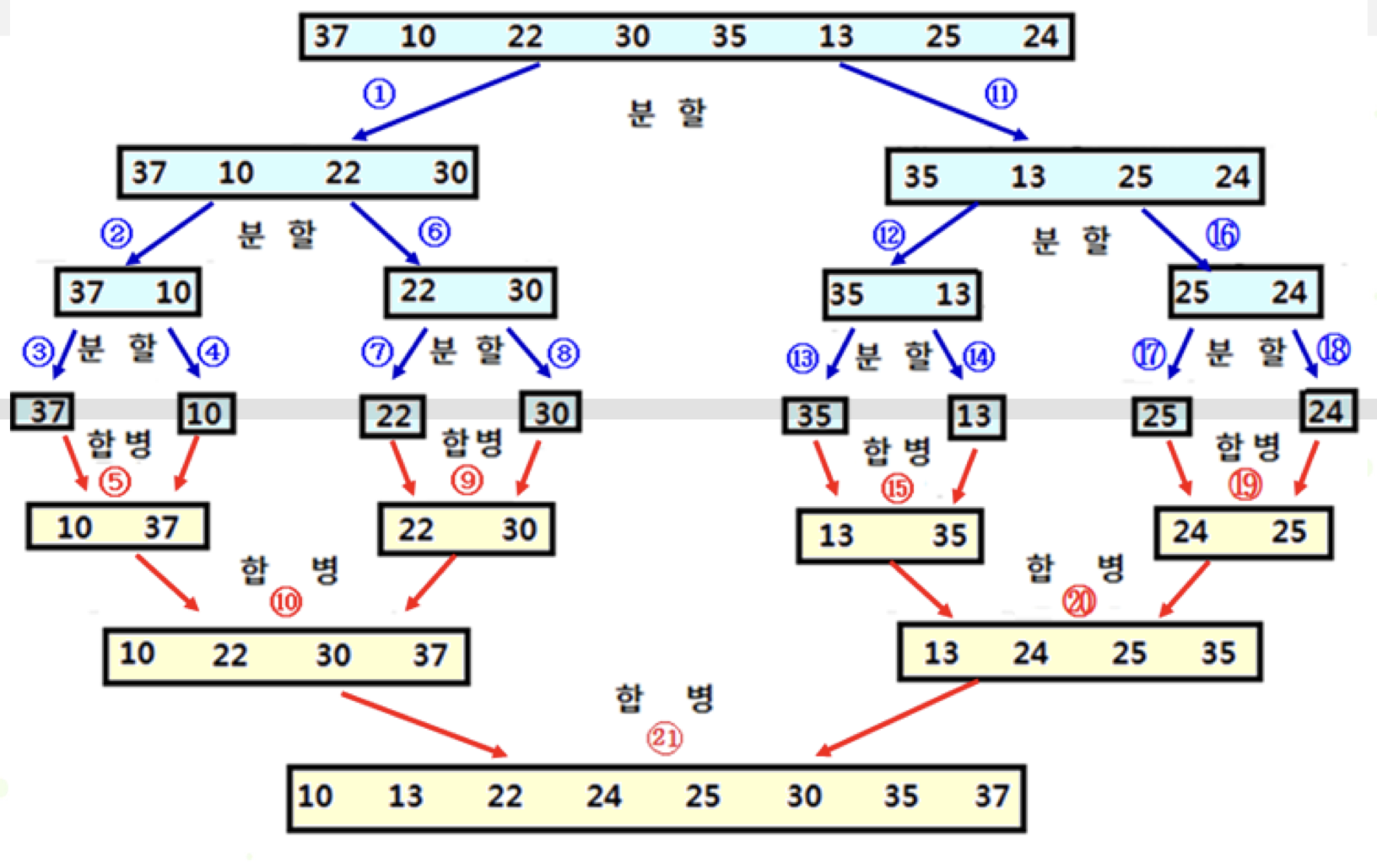
시간 복잡도 : (층수) O(n) = log2n O(n) =O(nlog2n)
📎2. Quick Sort
: 각 부분 문제의 크기가 일정하지 않은 형태의 알고리즘.
: pivot을 기준으로 피봇보다 작은 숫자들은 외편으로, 피봇보다 큰 숫자들은 오른편에 위치하도록 분할하고, 피봇을 그 사이에 놓는다.
각 부분문제들에 대해서도 동일한 과정을 순환호출해 정렬한다.
✏️psuedo code
QuickSort(A,left,right)
//입력 : 배열 A[left]~A[right]
//출력 : 정렬된 배열 A[left]~A[right]
if(left<right){
partition(A, left, right) //피봇을 기준으로 좌우 정렬 후 피봇의 자리를 옮김
QuickSort(A, left, p-1) //피봇보다 작은 그룹
QuickSort(A, p+1, right //피봇보다 큰 그룹
}
partition(A,left,right)
//입력 : A[left]~A[right]
//출력 : 피봇보다 작은 그룹과 큰 그룹으로 분할한 후 , 피봇이 위치한 원소의 인덱스 j
pivot = A[left], i =left+1, j=right
while i<=j
while(i<=j and A[i]<pivot) i = i+1 //피봇보다 크면 멈춤
while(i<=j and A[j]>pivot) j = j-1 //피봇보다 작으면 멈춤
if(i<j) then A[i] <-> A[j] //자리바꿈
A[left]<->A[j] //A[j]는 가장 오른쪽에 위치한 피봇보다 작은 수
return j //j는 최종적으로 피봇이 저장된 원소의 인덱스✏️수행과정
(랜덤 피봇으로 수행하였다.)
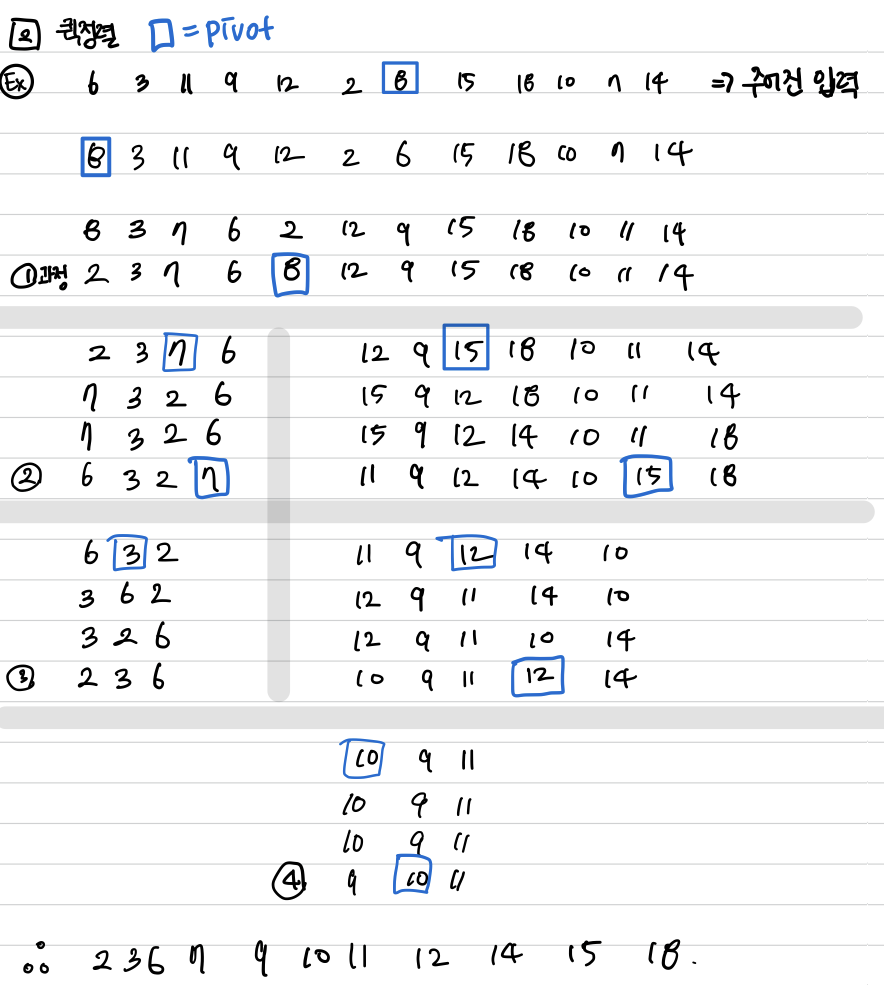
✏️ pivot 선택 방법
: 피봇의 선택에 따라 시간복잡도가 변하기 때문에 피봇 선정은 중요하다.
- 랜덤하게 선정
- 3 숫자의 중앙 값 (Median of Three)
- Median of Medians(Tukey's Ninther)
- 3등분한 후 Median of Three로 3개의 중앙값을 선정하고 세 중앙값들 중에서 중앙값을 피봇으로 정한다.
시간복잡도
- 최악경우 : O(n^2)
- 최선,평균경우 : O(nlog2n)
