프레셰 필터와 비표준 자연수

뢰벤하임-스콜렘 정리에 따르면 표준 산술 모형과 기초적으로 동등(elementarily equivalent)하지만 구조적으로 상이(nonisomorphic)한 모형이 존재한다. 달리 말해, 자연수가 만족하는 모든 1차 논리 명제를 만족하지만 자연수가 아닌 수 체계가 존재한다.

이 글(시리즈)에서는 초곱(ultraproduct)을 이용하여 대표적인 산술의 비표준적 모형인 초자연수(hypernaturals)를 구성하고, 이것이 표준 산술 모형과 기초적으로 동등함을 보증하는 워시의 정리(Łoś's theorem)를 증명한다.

1. 개괄

콤팩트성 정리에 의해 우리는 1차 논리가 유한과 무한을 구별하지 못함을 안다. 따라서 무한을 적절히 사용함으로써 자연수와 1차 논리적으로 구분 불가능한 모델을 정의할 수 있으리라 기대해봄직하다.

이에 따라 다음과 같이 초자연수 $[0], [1], [2], \dots$를 정의하자.

그런데 생각해 보면 모든 항이 0으로 차 있어야 $[0]$으로 간주하는 것은 지나치게 엄격하다. 예를 들어 처음 두 개의 항만 1이고 나머지 항은 모두 0인 튜플 $(1, 1, 0, 0, 0, \dots)$ 또한 $[0]$으로 보는 것이 자연스럽다. 따라서 유한 개의 항을 제외한 모든 항이 $n$이라면 그 튜플 또한 $[n]$으로 간주하도록 하자. 즉,

하지만 이제 다음의 문제가 생긴다. 다음 튜플은 $[0]$으로 간주해야 하는가, $[1]$로 간주해야 하는가?

이 모호함을 제거하기 위해 우리는 짝수 집합과 홀수 집합 중 하나를 임의로 채택할 것이다. 만약 짝수 집합을 채택했다면 위 튜플은 $[0]$이 되고(인덱스는 0부터 시작하는 것으로 전제한다) 홀수 집합을 채택했다면 $[1]$이 될 것이다.

하지만 이 채택의 과정에는 주의가 필요하다. 만약 6의 배수의 집합이 채택되었다면, 3의 배수의 집합 또한 채택되어야 논리적으로 일관된다. 후자를 만족하는 튜플은 자명하게 전자를 만족하기 때문이다. 그리고 3의 배수의 집합이 채택되었으므로, 3의 배수가 아닌 수의 집합은 기각되어야 한다. 자연수의 모든 부분집합에 대해 이같은 채택과 기각의 과정을 거친 결과물은 초필터(ultrafilter)라고 불리는 구조와 상응될 것이다. 적절한 초필터가 주어지면 그것을 토대로 임의의 튜플을 초자연수에 대응시킬 수 있으며, 이 전체적인 과정을 초곱(ultraproduct)이라고 부른다.

2. 초필터의 정의

정의. $X$가 집합이라고 하자. $X$의 부분집합들로 이루어진 집합 $\mathcal{F}$가 다음을 만족할 때, $X$의 필터라고 부른다.

1. $X \in \mathcal{F}$
2. $\varnothing \not\in \mathcal{F}$
3. 상위집합 닫힘: $A \in \mathcal{F}, A \subset B \implies B \in \mathcal{F}$
4. 유한 교집합 닫힘: $A, B \in \mathcal{F} \implies A \cap B \in \mathcal{F}$

직관적으로 필터는 "큰 집합들의 모임"이다. 이 관점에서 보면 1번과 2번 공리는 전체집합은 크고 공집합은 작다는 자명한 원리를 진술한다. 3번 공리는 큰 집합을 포함하는 집합은 크다는 원리를, 4번 공리는 큰 집합끼리 유한 번 교집합을 해도 여전히 크다는 원리를 진술한다.

여담으로 필터는 초곱뿐 아니라 퍼지 논리(fuzzy logic)의 모형을 고전 논리의 모형으로 변환하는 데도 쓰인다. 이때 필터는 "큰 집합들의 모임"이 아닌 "참인 문장들의 모임"이 된다. 그리고 퍼지 논리에서 고전 논리로의 변환은 코헨의 강제법을 이해하는 한 가지 방식이기도 하다.

하세 다이어그램(Hasse diagram)을 통해 필터를 더 직관적으로 이해할 수 있다. 색칠된 영역은 $X = \{ 0, 1, 2 \}$의 필터이다. 하세 다이어그램을 $\varnothing$에서 $X$로 가는 물줄기의 흐름으로 이해하면, 특정 지점에 잉크를 떨어뜨렸을 때 그 잉크가 퍼져 나가는 영역은 필터를 이룬다.

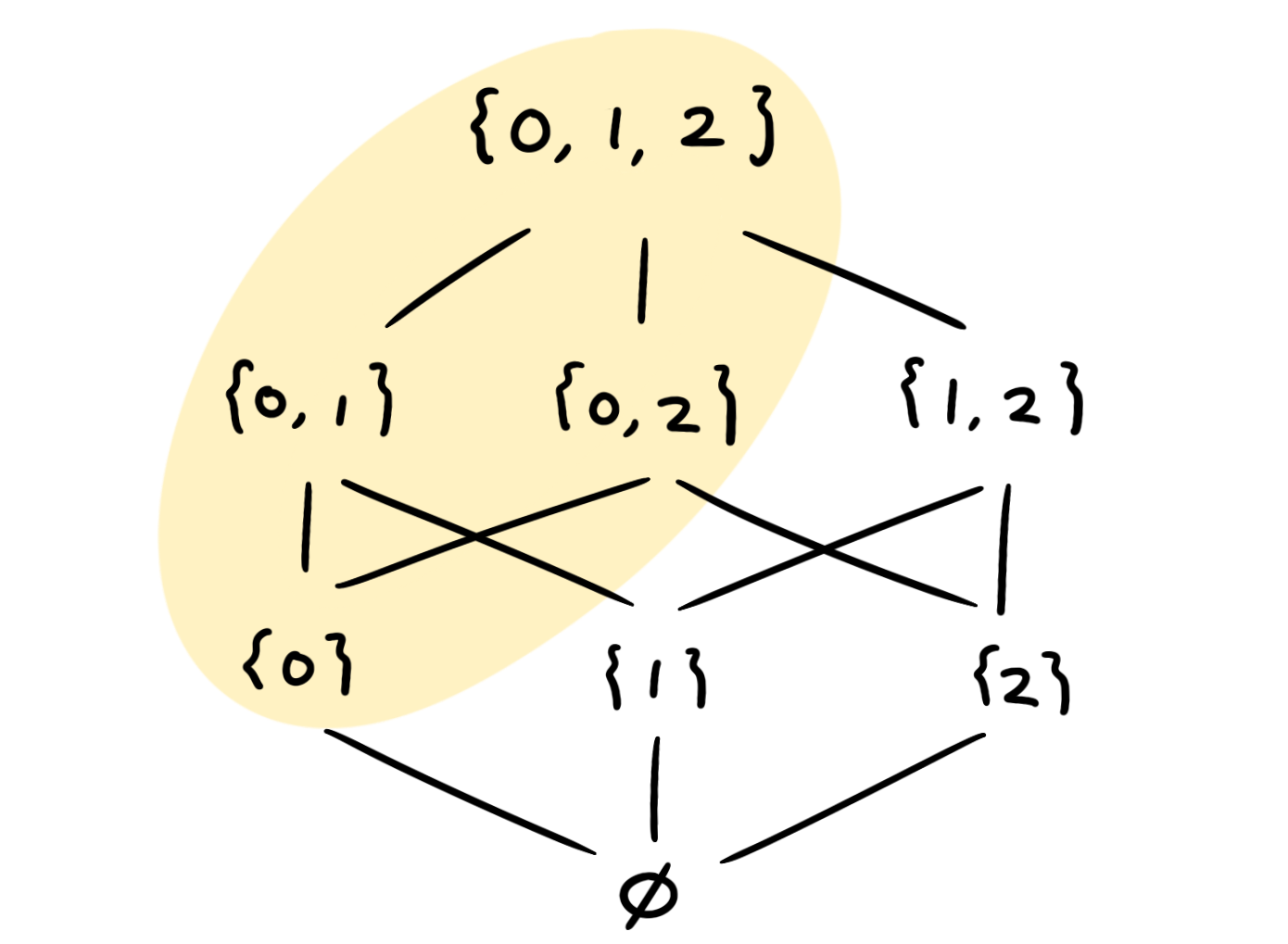
2번 공리와 4번 공리에 의해, $A \in \mathcal{F}$라면 $A^c \coloneqq X \setminus A \notin \mathcal{F}$이다. 이 사실을 강화하여, $X$의 모든 부분집합에 대해 그 집합 또는 여집합이 필터에 있을 것을 요구하면 초필터(ultrafilter)의 정의를 얻는다.

정의. $X$의 필터 $\mathcal{F}$가 다음을 만족할 때 $\mathcal{F}$는 초필터이다.

$\forall A \in \mathcal{P}(X) : A \in \mathcal{F} \lor A^c \in \mathcal{F}$

앞선 그림의 필터는 초필터이다. 초필터는 하세 다이어그램의 정확히 절반을 차지한다는 사실에 주목하라.

3. 무한집합에서의 초필터

최소(least) 원소를 가지는 필터를 주 필터(principal filter)라고 하며, 주 필터가 아닌 필터를 자유 필터(free filter)라고 한다. 지금까지 우리가 본 모든 필터는 주 필터로, "특정 지점에 떨어뜨린 잉크가 퍼져 나가는 영역"의 이미지와 완전히 부합한다.

주 필터와 달리 자유 필터는 직관적으로 포착하기 힘들다. 다음의 정리 때문이다.

정리. 유한집합 위의 필터는 모두 주 필터이다.

Proof. $A_0 \in \mathcal{F}$가 최소 원소가 아니라고 하자. 그러면 어떤 $B \in \mathcal{F}$가 존재하여 $A_1 = A_0 \cap B \subsetneq A$이다. 즉, $| A_1 | < |A_0 |$이다. $A_1$이 최소 원소라면 증명이 끝나고, 아니라면 똑같은 과정을 반복한다. 주어진 집합의 크기가 유한하므로 이 과정은 계속 반복될 수 없으며, 최소 원소에 종착하게 된다. ■

위 정리는 이렇게 이해할 수도 있다. 자유 필터는 그 내부에 무한히 이어지지만 (따라서 유한 교집합만으로 최소 원소에 도달할 수 없다) 공집합에 도달하지는 않는 부분집합의 체인을 가지는 필터이다. 이에 따라 무한집합 위의 필터만이 자유 필터가 될 수 있다.

그 실례를 살펴보자.

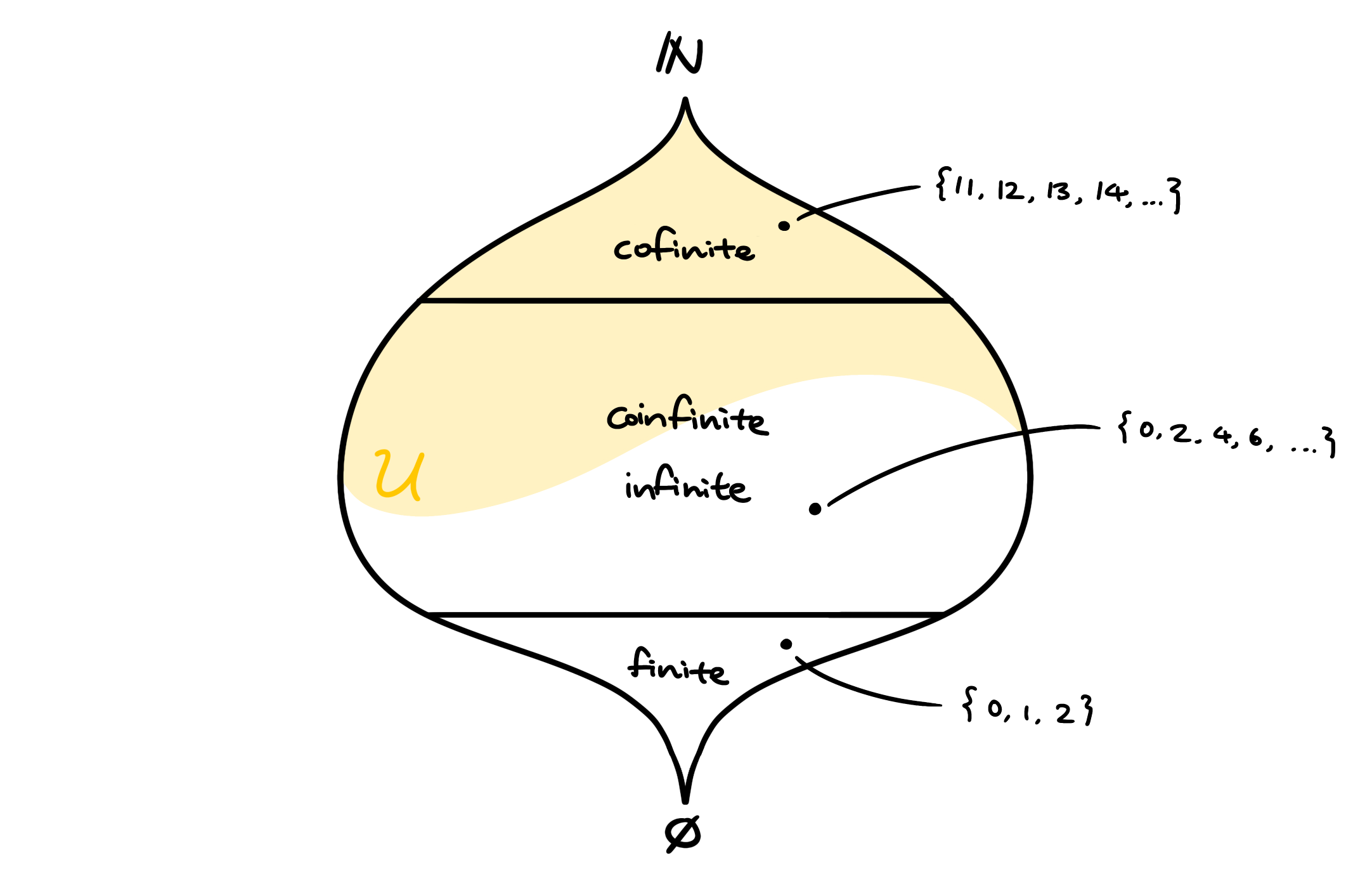
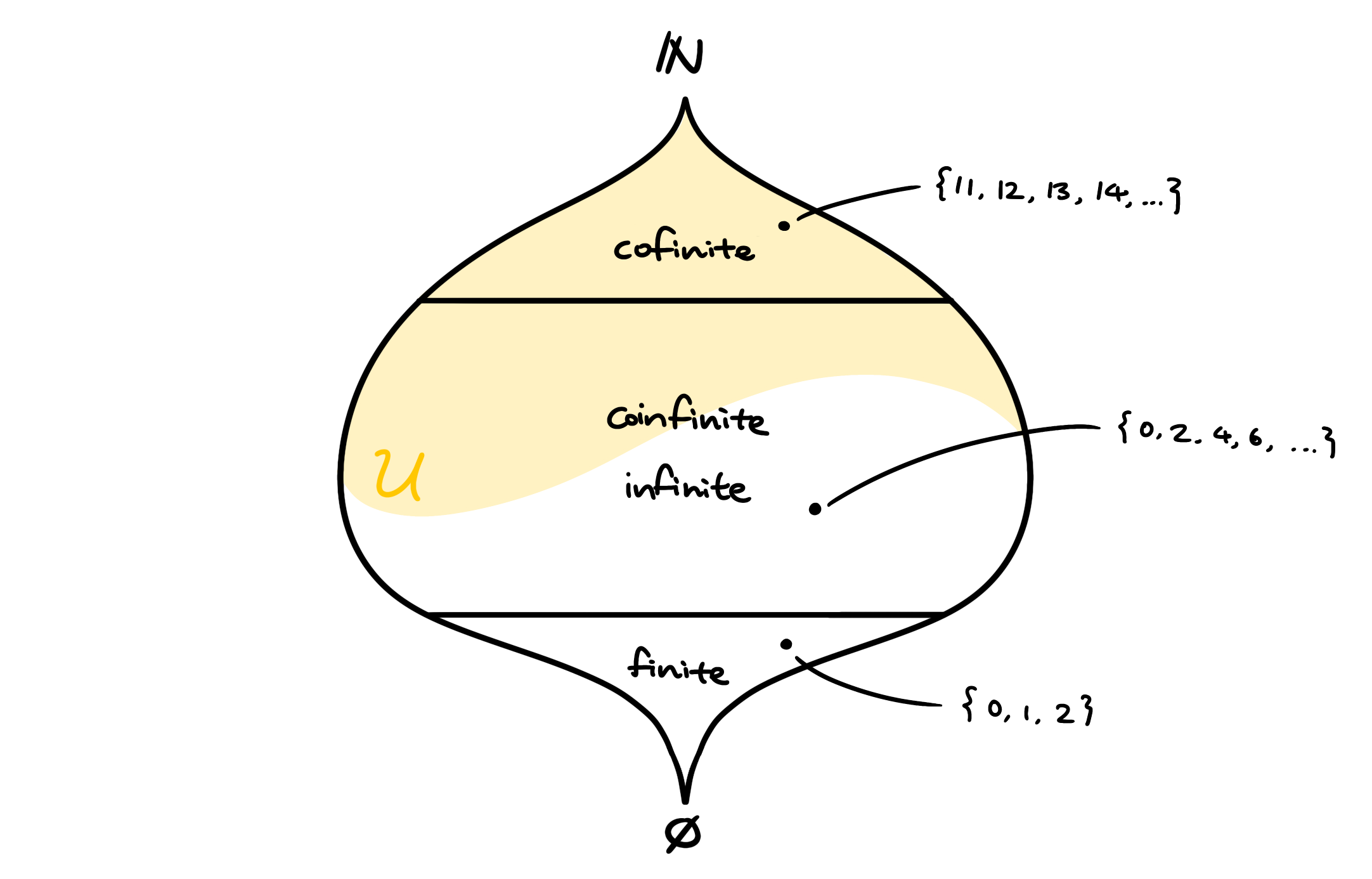
정의. $X$가 무한집합이라고 하자. $A \subset X$가 여유한(cofinite)하다는 것은 $X \setminus A$가 유한집합인 것이다.

정리. $\mathbb{N}$의 모든 여유한 부분집합의 모임을 $\mathcal{F}$라고 하자. $\mathcal{F}$는 자유 필터이다.

증명은 연습문제로 남긴다. 위 정리의 $\mathcal{F}$를 프레셰 필터(Fréchet filter)라고 부른다. 일례로 10보다 큰 수들의 집합 $\{ 11, 12, 13, 14, \dots \}$은 $\mathcal{F}$의 원소이지만, 짝수의 집합은 $\mathcal{F}$의 원소가 아니다.

프레셰 필터는 초필터가 아니다. 하지만 다음 정리에 의해 초필터로 확장할 수 있다.

정리. 모든 필터는 초필터로 확장될 수 있다.

Proof. $X$의 모든 필터들의 모임 $\Omega$에 포함 관계로 정의되는 순서를 주자. 이 순서 하에서 체인을 이루는 필터들의 합집합은 필터임을 어렵지 않게 보일 수 있다. 따라서 초른의 보조정리에 의해 $\Omega$는 극대(maximal) 원소 $\mathcal{U}$를 가진다. 만약 $\mathcal{U}$가 초필터가 아니라면, 어떤 $A_0 \subset X$가 존재하여 $A_0, A_0^c \notin U$이다. 이제 다음과 같이 $\mathcal{V}$를 정의한다.

$\mathcal{V}$는 필터임을 확인할 수 있다. 이것은 $\mathcal{U}$의 극대성에 위배된다. 따라서 $\mathcal{U}$는 초필터이다. ■

따라서 자연수 집합은 프레셰 필터로부터 확장되는 자유 초필터를 가진다. 이 필터를 프레셰 초필터라고 부르자.

4. 초자연수

지금까지의 논의를 정리하자면, 프레셰 초필터를 비롯한 자유 초필터는 다음의 성질을 가진다.

1. 모든 여유한 집합을 원소로 가진다.
2. 유한집합은 원소로 가지지 않는다.
3. $A \subset \mathbb{N}$일 때 $A$가 필터의 원소이거나 $A^c$가 필터의 원소이다.

위 세 성질 덕분에 프레셰 초필터는 서론에서 초곱의 기초적인 아이디어를 개괄했을 때 맞닥뜨렸던 모호성의 문제를 해결하는 데 안성맞춤이다. 이제 우리는 다음과 같이 초자연수를 정의할 수 있다.

$\mathcal{U}$가 자유 초필터라고 하자. $\mathbb{N}^\omega$ 위에 다음의 동치 관계를 정의한다.

이것이 동치 관계임은 어렵지 않게 확인할 수 있다. 따라서 다음과 같이 동치류를 취할 수 있다.

$\mathbb{N}^*$을 초자연수(hypernaturals)라고 한다. 초자연수의 정의가 동치류인 것은 서론에서 초자연수를 $[n]$으로 적은 이유이다. 이제 남은 것은 초자연수의 연산과 술어 관계를 정의하는 것이다.

초자연수의 덧셈은 다음과 같이 자연스럽게 정의한다.

여기에는 한 가지 미묘한 문제가 있다. 초자연수의 정의가 동치류이기 때문에, 동치류의 어떤 원소를 택하더라도 위 덧셈의 결과에 영향을 주지 않음을 보여야 한다. 즉,

에 대해,

임을 보여야 한다. 다행히 이는 어렵지 않다.

곱셈과 역원 또한 비슷하게 정의하면 된다. 한편 $<$와 같은 이항 관계는 다음과 같이 정의한다.

이 정의는 자연스럽게 삼항, 사항 관계로 일반화할 수 있다.

이로써 우리는 초자연수를 정의했다. 다음 글에서는 초자연수의 여러 비표준적인 특징과, 그런 비표준성에도 불구하고 초자연수와 자연수를 1차 논리로 구분할 수 없음을 보이는 워시의 정리를 살펴볼 것이다.