6절. 정규화 선형회귀
정규화 선형회귀 방법은 선형회귀 계수(Weight)에 대한 제약 조건을 추가해서 모형이 과도하게 최적화되는 현상, 즉 과적합(Overfitting)을 막는 방법이다.
모형이 과도하게 최적화되면 모형 계수의 크기도 과도하게 증가하는 경향이 있다.
그래서 정규화 방법에서 추가하는 제약의 조건은 계수의 크기를 제한하는 방법이 사용된다.
정규화모형은 회귀분석에 사용된 데이터가 달라져도 계수가 크게 달라지지 않도록 한다.
6.1. 정규화 선형회귀모형
계수의 크기를 제한하는 방법으로 다음과 같은 세가지 방법이 사용된다.
- Lasso 회귀모형(L1 정규화)
- Ridge 회귀모형(L2 정규화)
- Elastic Net 회귀모형 (Lasso+Ridge, L1_wt=0.5)
1) Lasso 회귀모형
가중치의 절댓값의 합을 최소하는 것을 추가적인 제약조건으로 검
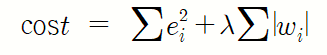
2) Ridge 회귀모형
가중치들의 제곱합을 최소화
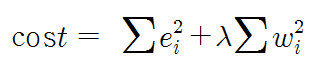
3) Elastic Net 회귀 모형
가중치의 절댓값의 합과 제곱합을 동시에 제약조건으로 가지는 모형
이 모형은 두개의 하이퍼 매개변수를 가진다.
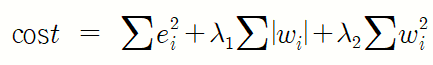
6.2. statsmodels의 정규화 회귀모형
하이퍼 파라미터는 다음과 같이 모수(alpha)와 L1_wt에 의해 정의된다.
alpha는 하이퍼파라미터로 alpha가 크면 정규화 정도가 커지고 가중치들의 값이 작아진다.
예제에 사용할 데이터셋을 생성
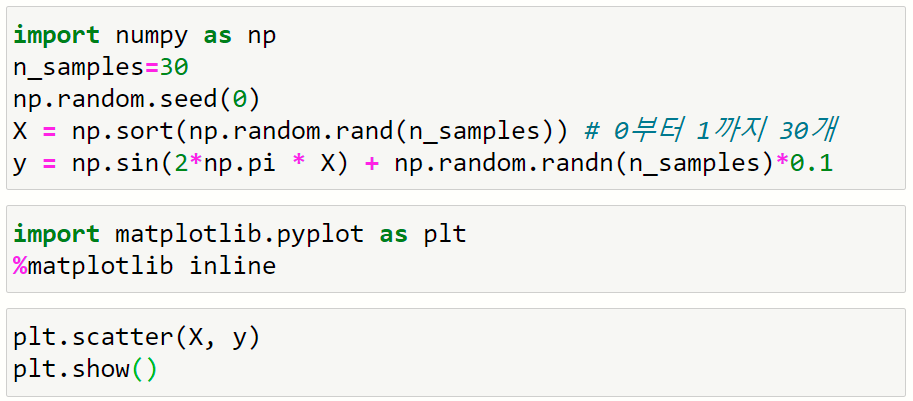
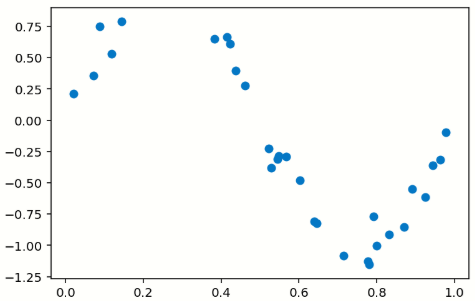
앞에서 만들어진 데이터 X,y를 이용해서 데이터프레임을 만들고 선형회귀식을 만든다.
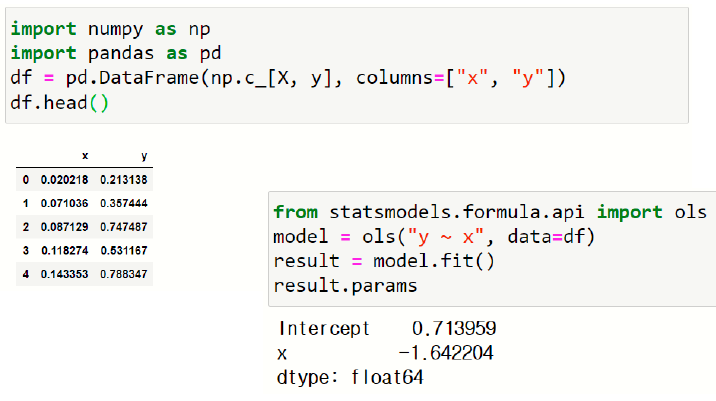
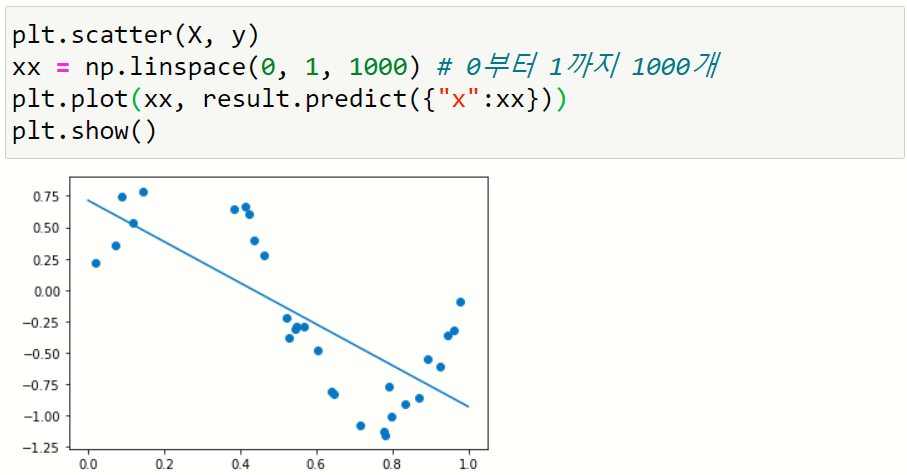
산점도 그래프를 표시하고 선형회귀식을 시각화한다.
1) 정규화를 하지 않는 회귀모형
2) Lasso 회귀모형
3) Ridge 회귀모형
7절. 다중회귀 분석
회귀분석은 표준 회귀분석, 위계적 회귀분석, 단계적 회귀분석, 로지스틱 회귀분석 등과 같이 종류가 매우 다양하다.
그중 다중회귀분석은 단순회귀분석의 확장판으로 선형회귀모형을 기초로 독립변수가 2개 이상일 때 사용된다.
7.1. 다중 회귀의 변수 추정
독립변수는 영향을 미치는 변수, 즉 원인 변수이며 종속변수는 영향을 받는 변수, 결과변수이다.
그러므로 서로 논리적으로 타당성이 있는 변수를 독립변수와 종속변수로 설정해야 한다.
다중 회귀분석에서 가장 기본적인 업무는 상수와 베타회귀계수를 구하는 것이다.
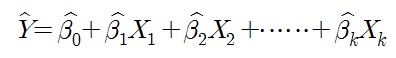
^(hat, 추정자) = 잔차
종속변수와 독립변수와의 관계를 밝히는 통계모형에서 모형에 의하여 추정된 종속변수의 값과 실제 관찰된 종속변수 값과의 차이를 의미한다.
이 차이는 오차(error)로도 해석되며 통계모형이 설명하지 못하는 불확실성 정보이다.
그러나 회귀분석의 결과만으로는 인과관계를 규명할 수없다. 논리적 근거가 있어야 함
7.2. 다중회귀분석 예
1) 데이터 준비
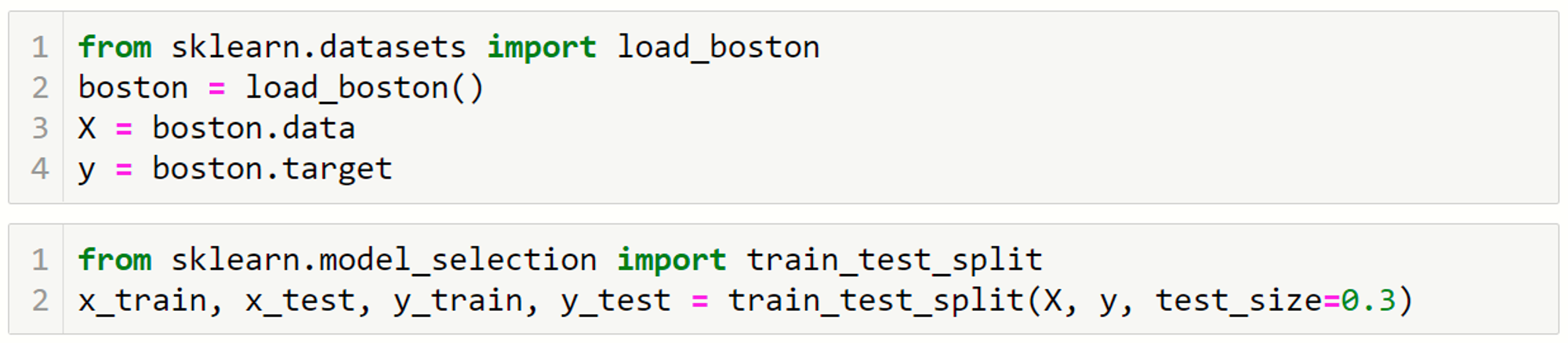
2) 회귀 모형

3) 학습 데이터셋을 이용한 평가
학습 데이터셋을 이용해서 모형을 평가한다.
- 회귀모형의 score() 함수를 이용
- sklearn.metrics 모듈의 평가함수를 이용
- cross_val_score() 함수의 scoring 속성을 이용
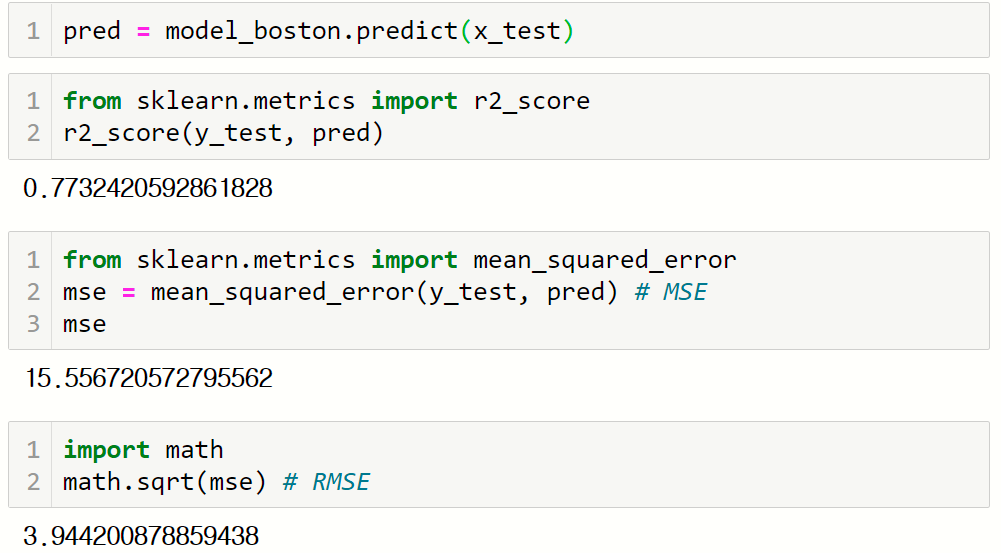
다음 코드는 모형의 score()함수를 이요해서 학습 데이터셋을 이용해 학습시킨 모형을 평가한다.
출력된 결과는 결정계수(R2)이다.

메트릭 함수를 이용해 모형을 평가한다. 평가에 사용할 메트릭 함수는 MSE를 출력하는 mean_squared_error() 함수이다. 이 결과에 루트를 씌워 RSER를 출력할 수 있다.
4) 예측하기
다음코드는 모형을 이용해 평가용 데이터셋을 입력해서 y를 예측한다.

5) 평가 데이터셋을 이용한 평가
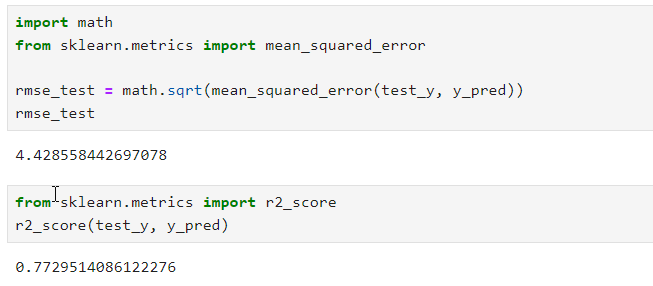
학습용 데이터셋의 결정계수와 RMSE는 평가용 데이터셋의 결정계수 및 평균과 큰 차이를 보이지 않는다.
7.3. 다중회귀식의 추정방법
- 동시 입력법
모든 독립변수들을 포함하여 분석하는 방법
이를 통해 특정 독립변수의 영향력을 알 수 있음 - 단계적 선택법
다른 변수들이 회귀식에 존재할 때 종속변수에 영향력이 있는 변수들만을 회귀식에 포함시키는 방법
설명력이 높은 즉, 유의 확률 p가 가장 작은 변수의 순으로 회귀식에 포함시킴 - 제거법
독립변수가 없이 절편(상수항, bias)으로 구성된 모형을 만듬 - 후진 소거법
모든 독립변수를 모두 포함시킨 상태에서 기여도가 적은 변수부터 하나씩 제거해서 모델에 남아있는 변수들의 유의확률이 유의수준 이하가 될 때까지 삭제하는 방법 - 전진 선택법
독립변수가 하나도 포함되지 않은 모델에서 시작해서 F 값에 가장 큰 기여를 하는 변수(유의확률 p가 가장 작은)를 순서대로 하나씩 더해가는 방법
데이터 불러오기
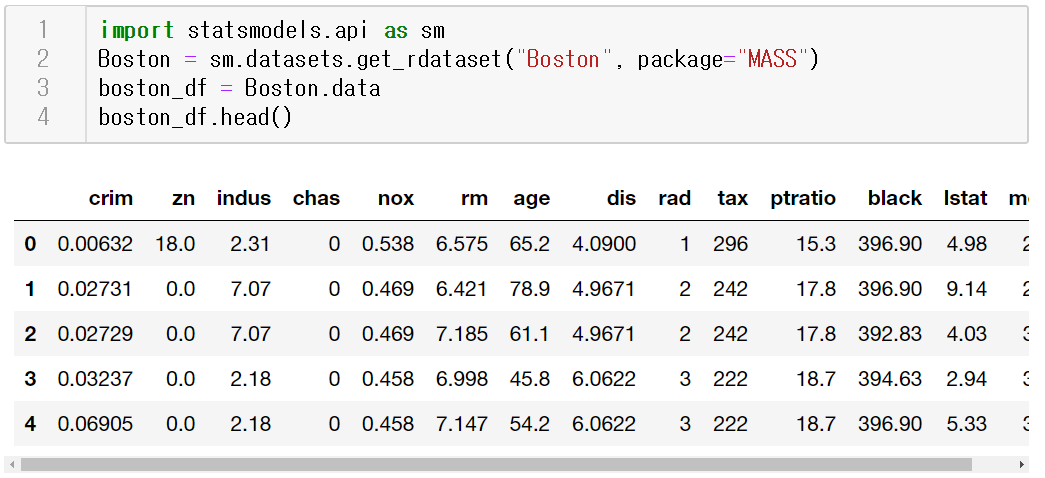
medv ~ join 코드는 모든 변수를 이용해 모형을 생성하고 요약정보를 출력한다.
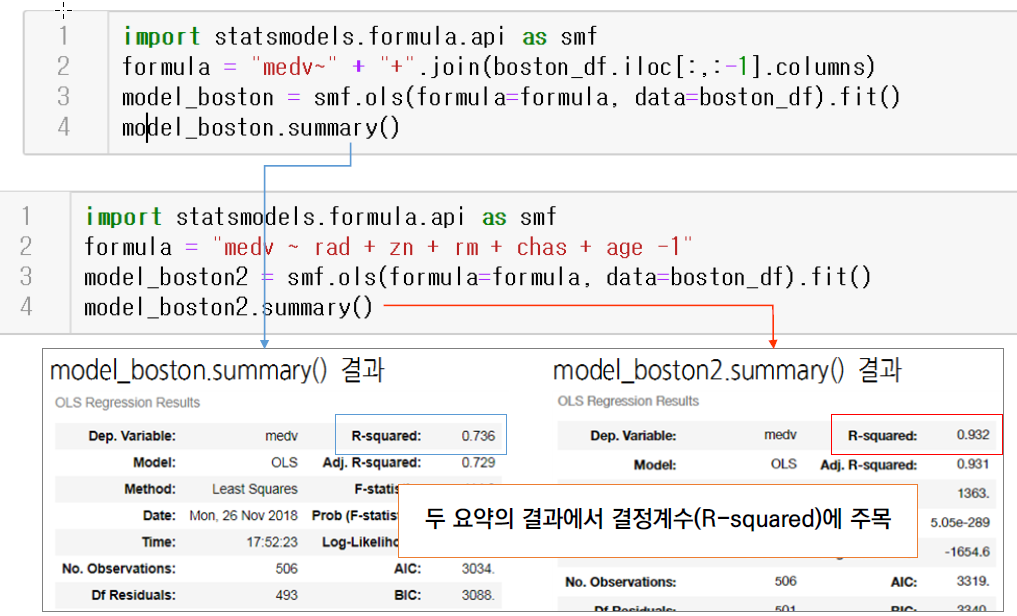
모든 변수를 사용했을 경우보다 일부변수를 사용해서 회귀모형을 만들었을 경우의 결정계수가 더 높은 것을 알수 있다.
7.4. 상관계수와 결정계수
상관분석에서 상관관계의 정도를 나타내는 계수가 바로 상관계수였다.
단순회귀에서는 상관계수를 제곱한 값이 결정계수(R2)이다.
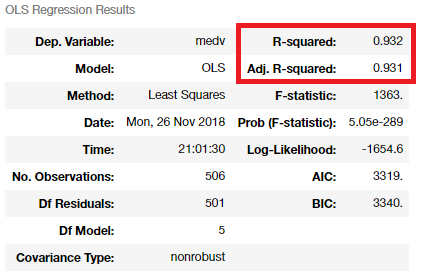
7.5. AIC와 BIC
AIC 와 BIC를 이용해서 모형이 적합도가 더 높은것을 찾을 수 있다.
AIC는 값이 작을수록 모형의 적합도가 높다.
BIC는 회귀계수의 수에 더해 표본의 크기 n에 대해서도 패널티를 부가한 것이다.
7.6. 잔차의 독립성
- 회귀분석의 기본 가정 사항 중 잔차의 독립성이 있음
- 잔차가 다른 잔차에 영향을 미치게 되는 경우를 자기상관(Autocorrelation)이라고 하는데 자기상관이 높으면 분석의 신뢰성을 잃게 됨
- 자기상관은 앞의 잔차항이 뒤의 잔차항에 영향을 미치는 경우로 주로 시계열 자료에서 많이 관찰됨
- 회귀모형에서 자기상관이 발생하게 되면, 회귀모형의 기본가정인 ‘잔차항들은 서로 독립이다’라는 가정을 위배하게 됨
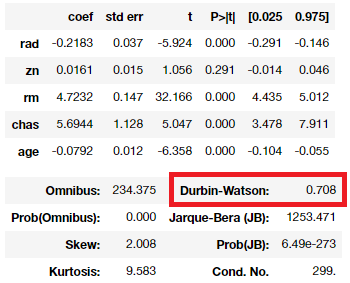
- 잔차의 독립성은 Durbin-Watson(더빈 왓슨)값으로 판단하게 되는데 0에 가까울수록 양의 자기상관, 4에 가까울수록 음의 자기상관이 있다고 판단하며,2에 가까울수록 자기 상관이 없다고 판단
- 보통 1.5 ~ 2.5 사이의 값을 적용. 더빈 왓슨은 오차항에 자기상관이 있는지 없는지를 판단하기 위해 사용
7.7. 잔차의 정규성
정상성 : 오차가 정규분포를 따라야 한다는 것, 잔차의 정규성이라고도 함
잔차의 정규성을 확인하는 지표로 Omnibus와 Jarque-Bera가 있다.
- 귀무가설: 잔차항은 정규분포를 따른다.
- 대립가설 : 잔차항은 정규분포를 따르지 않는다.
이 두 검정의 p값이 유의수준(0.05)보다 크면 잔차항이 정규분포를 따르므로 귀무가설을 채택한다. 쉽게 말하면 이 두 값이 0.05보다 크면 문제될 것이 없다.
