6월 3일자에 들은 수업 내용을 정리한 글입니다.
회귀분석, 상관분석에 대한 개념을 정리하였습니다.
1절. 회귀분석 개요
1.1. 회귀분석 정의
💡 회귀분석 : 관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한 뒤 적합도를 측정(평가)해내는 분석weight와 bias 모형은 모델의 구조와 파라미터를 가지고 있음
모형 → 어떤 수식과 파라미터, 구조를 가지고 있는 모델 이라 이해하면 됨
- 회귀 분석 (regression analysis) 회귀분석은 선형적인 상관성을 가진 변수들 사이의 인과관계를 증명하는 것
원인이 되는 독립변수, 결과가 되는 종속변수
회귀분석은 시간에 따라 변화하는 데이터나 어떤 영향, 가설적 실험, 인과 관계의 모델링 등의 통계적
예측에 이용될 수 있음
어떤 연관성을 가지고 있는 종속변수의 변동이나 분산을 설명하기 위하여 종속변수와 관계가 있는 독립
변수들 중 각각의 독립변수가 설명력을 얼마나 가지고 있는가를 결정할 때 사용
1.2. 회귀분석을 위한 전제 사항 ✔
선형성 : 독립 변수의 변화에 따라 종속 변수도 일정 크기로 변함
독립성 : 오차와 독립 변수의 값이 관련이 없음
등분산성 : 독립 변수의 모든 값에 대해 오차들의 분산이 일정(일정하지 않은 경우 과적합)
비상관성 : 관측치의 오차들 사이에 상관관계가 없음
정상성 : 오차가 정규 분포를 따름
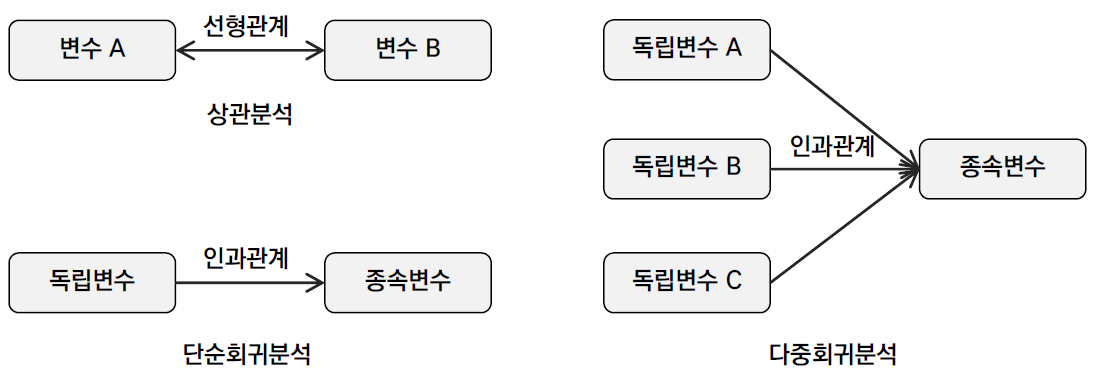
1.3. 상관분석, 단순회귀분석, 다중회귀 분석
상관분석 : 두 변수 사이의 원인과 결과가 아닌 서로 상관적 영향이 있는지 분석하는 것
회귀분석 : 인과관계로서 독립변수가 종속변수에 얼마만큼 영향을 주는지를 분석하는것
단순 회귀 분석 : 독립변수가 1개이며 종속변수도 1개인 것
다중 회귀 분석 : 만일 독립변수가 2개 이상인 경우의 회귀분석
2절. 분포와 추론
2.1. 표본과 실험
통계 분석 시 모집단, 표본, 모평균, 표본 평균 등 용어를 사용함 이에 대한 용어를 먼저 설명
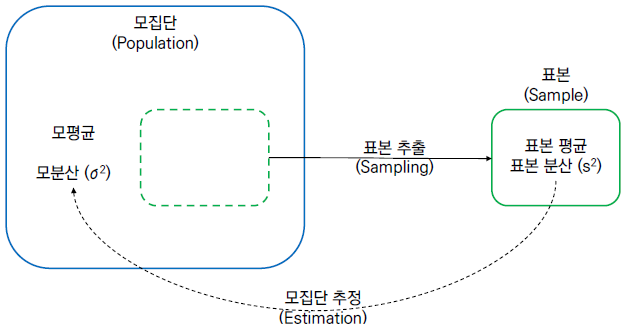
1) 모집단과 표본
모집단(Population) : 조사하고자 하는 대상 집단 전체를 의미
모집단에서 조사하기 위해 뽑은 모집단의 일부 원소를 표본(Sample)이라고 함
이때 표본의 개수를 표본의 크기라고 부른다.
모수(parameter) : 모집단에 대한 정보
2) 실험
특정 목적 하에서 실험 대상에게 처리를 가한 후에 그 결과를 관측해 자료를 수집하는 방법
측정(Measurement) : 추출된 원소들이나 실험 단위로부터 주어진 목적에 적합하도록 관측해 자료를 얻는 것

2.2 분포
분포를 설명하기 전에 먼저 확률변수(random variable)에 대한 이야기를 해야 한다.
확률 변수는 표본공간의 각 단위 사건에 실수값을 부여하는 함수를 의미한다.
확률변수는 이산형 확률변수(discrete random variable)와 연속형 확률변수(continuous random variable)가 있다.
이산형 확률변수는 확률값을 갖는 값이 셀 수 있는 변수를 의미하며, 연속형 확률변수는 가능한 값이 실수의 어느 특정 구간에 해당하는 변수를 의미한다.
확률 분포(probability distribution)는 확률 변수가 가질 수 있는 모든 값과 그 값들이 나타날 확률을 나열한 표 or 그림 or 함수식 이다.
1) 이산형 확률 분포
이산형 확률변수(discrete random variable)는 0이 아닌 확률 값을 갖는 실수값이 셀수 있는 경우를 의미한다. 이산형 확률변수에서는 확률 질량 함수(probability mass function)가 사용되는데 이것은 각 이산점에 있어서 확률의 크기를 표현하는 함수를 의미한다.
베르누이 분포, 이항분포, 기하분포, 다항분포, 포아송 분포 등이 있다.
2) 연속형 확률 분포
연속형 확률변수(continuous rnadom variable)는 가능한 값이 실수의 어느 특정 구간 전체에 해당하는 확률변수를 의미한다. 연속형 확률변수에서 확률 밀도 함수(probability density function)가 사용되는데, 연속형 확률변수 X의 확률함수 f(x)를 의미한다.
균일(균등)분포, 정규분포, 지수분포, t-분포, x^2 분포, F-분포 등이 있다.
2.3. 추정과 가설검정
통계적 추론(Statistical inference)은 수집된 자료를 이용해 대상집단(모집단)에 대해 의사결정을 하는것을 의미한다. 통계적 추론 시에 추정(Estimation)과 가설검정(Hypothesis test)이라는 말을 많이 사요한다.
가설검정(Hypothesis test)은 모집단의 모수에 대한 어떤 가설을 설정한 후에 표본관찰을 통해 그 가설의 채택 여부를 결정하는 분석 방법이다.
1) 추정과 신뢰수준
추정은 점추정(Point estimation)과 구간추정(Interval estimation)이 있다.
점추정은 ‘모수가 특정한 값일 것’이라고 추정하는 것이며, 구간추정은 ‘확률로 표현된 신뢰도에서 모수가 특정한 구간에 있을 것’이라고 선언하는 것이다.
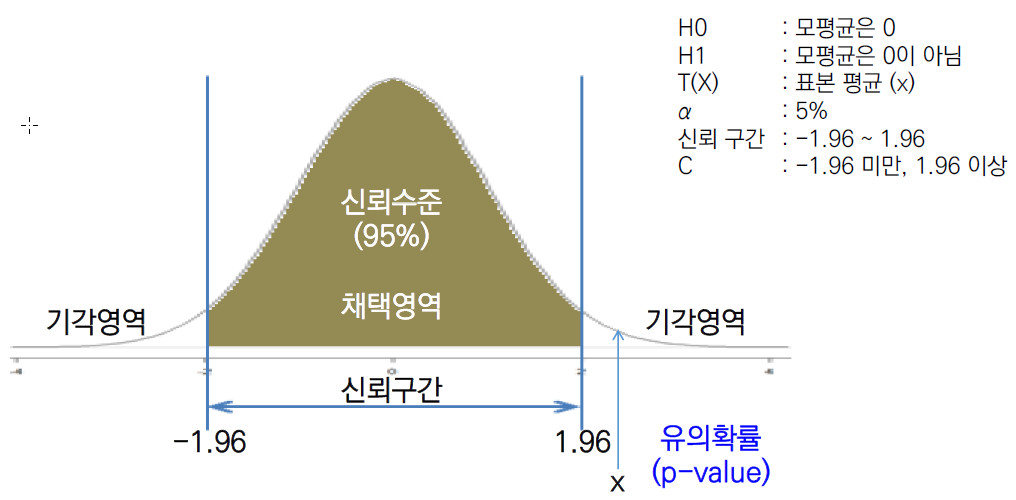
2) 귀무가설과 대립가설
귀무가설(Null hypothesis, H0) : 검정하고자 하는 모수에 대한 가설이며, 버릴 것을 예상하는 가설
대립가설(Altermative hypothesis, H1) : 연구자가 연구를 통해 입증되기를 기대하는 예상이나 주장을 대립가설로 내세움
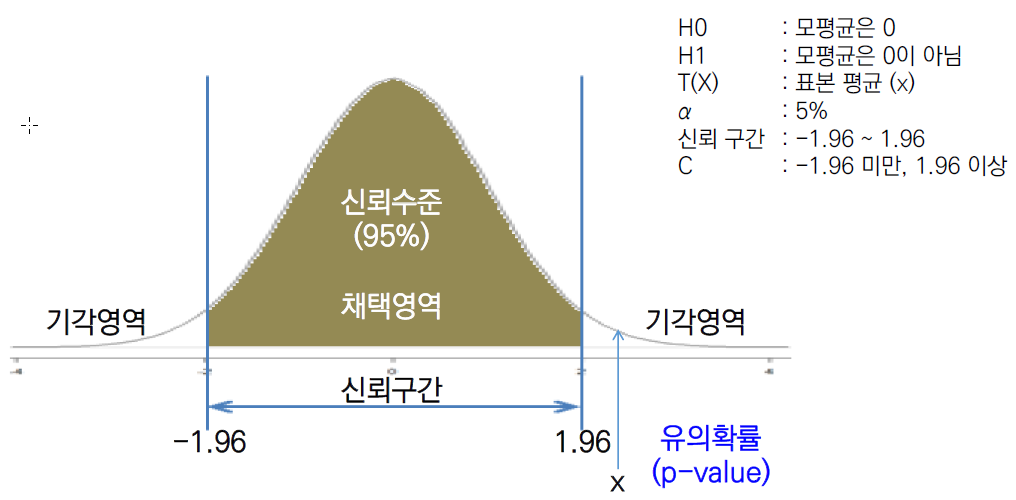
2.4. 유의수준과 유의확률
검정에 사용되는 통계량을 검정통계량(Test Statistic, T(x))이라고 하는데,귀무가설이 옳다는 전제 하에서 검정통계량 값을 구한 후에 이 값이 나타날 가능성의 크기에 의해 귀무가설 채택 여부를 결정한다.
1) 유의수준
유의수준(Significance level, 알파)은 검정 통계량의 값이 나타날 가능성이 ‘크다’ 또는 ‘작다’의 판단 기준이 된다. 이것은 ‘귀무가설이 옳은데도 이를 기각하는 확률의 크기’로 정의한다.
가설검정의 오류에는 제 1종 오류와 제 2종 오류가 있다.
제 1종 오류는 옳은 귀무가설을 기각하는(잘못된 대립가설을 채택하는) 오류를 말함
제 2종 오류는 옳지 않은 귀무가설을 채택하는 (맞는 대립가설을 기각하는) 오류를 말한다.
2) 유의확률
신뢰수준이 95%일 경우 유의확률(p-value)이 유의수준(0.05)보다 작으면 귀무가설을 기각한다.
이것은 대립가설을 채택하는 것을 의미한다.
2.5. 독립성 검정
독립성 검정은 단일 무작위 표본에서 추출한 자료에 대해 하나의 특성이 다른 특성과 독립적인지 여부를 알아보는 검증 방법이다. 범주(category)별로 빈도(frequency)만이 주어진 범주형 데이터의 분석은 일반적으로 카이제곱 분포를 이용한 검정법을 사용한다.
독립성 검정을 하는 목적
적합성 : 표본의 관측도수와 도집단의 기대도수를 비교하여 기대도수와 관측도수의 차이가 있는지를 검정
독립성 : 두 속성 사이에 관계가 있는지 검정
동질성 : 두 개 이상의 다항분포가 동일한지 검정(독립성 검정과 같은 방식이나 분석목적과 표현이 다름)
1) 피셔의 검정
데이터의 수가 적은 경우에 사용한다.
예를 들어, 대서양과 인도양에서 몇일간 지낸다고 가정했을 때 해당 표에 있는 것과 같은 정보로 대서양에 고래가 더 많이 살고 인도양에 상어가 더 많이 살고 있다고 할수 있을까?
| Atlantic | Indian | |
|---|---|---|
| whales | 8 | 2 |
| sharks | 1 | 5 |
다음은 이 데이터를 이용해서 피셔의 검정으로 p-value를 찾는다.
from scipy.stats import fister_exact
oddsratio. pvalue = fisher_exact([[8,2], [1,5]])
print(oddsratio, pvalue)
>> 20.0 0.0349650... 2) 맥니마 검정
교차표의 동질성을 테스트하는 검정으로 두 경우의 데이터가 얼마만큼 일치하는지 확인
기술적으로 교차표의 동질성(특히 한계 균질성)이라고 한다. 맥니마 검정은 치료 효과를 대조군과 비교하기 위해 의학에서 널리 사용된다.
K-fold 교차 검사와 같은 반복 평가와 다르게 한번에 한번만 평가될 수 있는 경우 맥니마 검정을 수행하는 것이 좋음.
여기서 말하는 한번만 실행할 수 있는 알고리즘의 경우 맥니마 검정은 허용 가능한 1종 오류가 있는 유일한 테스트이다.
2.6. 적합도 검정
k 개 범주를 가지는, 한개의 요인에 대해서, 이론적 분포를 따르는지 검사
콩 A,B,C는 3개 범주, 유전적 이론, A:20, B:30, C:50 (기대도수)
수확한 콩은 A:19, B:41, C:40 개가 수확되었음(관측도수)
H1: 적어도 하나의 범주는 ... 다르다
H0: ... 같다.
기대도수와 관측도수의 차이를 검정할 때 카이제곱 검정을 사용
멘델의 주장은 옳지 않다.
3절. 상관분석
상관분석은 두 변수 간에 선형적 관계가 있는지 분석하는것이다. 이에 사용하는 수치는 피어슨 상관계수, 켄달의 상관계수, 스피어만 상관계수가 있다.
3.1. 피어슨 상관계수
피어슨 상관계수(Pearson corrlation coefficient)는 수치로 표시된 데이터들의 상관관계를 확인하기 위해 사용된다.
두 변수가 모두 연속형 자료일 때 두 변수간 성형적인 상관관계의 크기를 모수적(parametric)인 방법으로 나타낸 값이다.
피어슨 상관계수는 -1 ~ 1 사이의 값을 가지며 일반적으로 0.7이상이면 매우 강한 양의 상관관계 -0.7 이하면 매우 강한 음의 상관관계를 갖는다.
p-value를 이용하여 상관계수의 유의성을 확인할 수 있다.
귀무가설과 대립가설은 아래와 같이 정한다.
귀무가설(H0) : 상관계수가 0 (상관관계가 없음)
대립가설(H1) : 상관계수가 0이 아님 (상관관계가 있음)
유의확률(p-value)가 유의수준가 0.05보다 작은 경우, 귀무가설을 기각한다.
3.2. 스피어만 상관계수
스피어만 상관계수는 상관관계를 분석하고자 하는 두 연속형 변수의 분포가 심각하게 정규분포를 벗어난다거나 두 변수가 순위 척도 자료일 때 사용하는 값이다.
데이터가 서열 척도인 경우 값 대신 순위를 사용하여 계산한 상관계수이다.
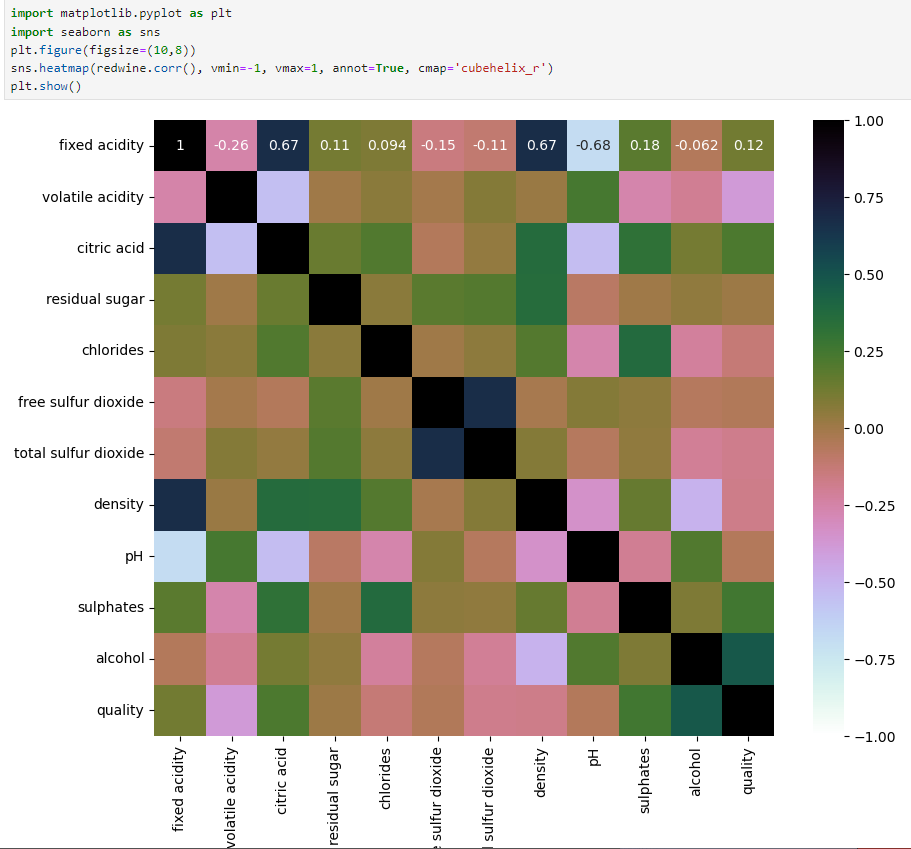
corr() 함수의 인수로 method=’spearman’을 포함하면 스피어만 상관계수를 얻을 수 있다.
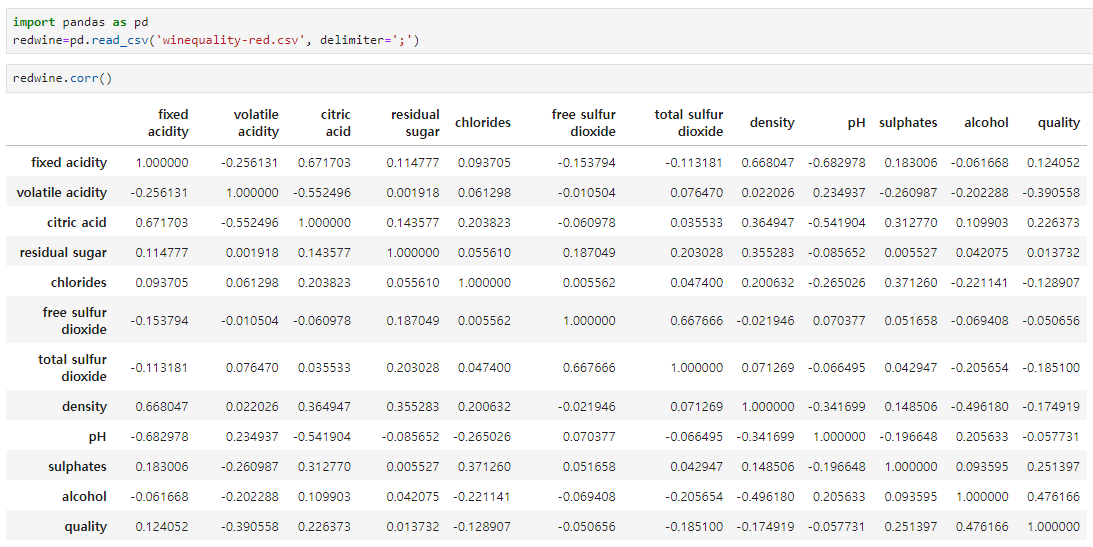
from scipy.stats.stats 모듈의 spearmanr()함수를 이용해도 스피어만 상관계수를 구할 수 있다.
4절. 단순 회귀분석
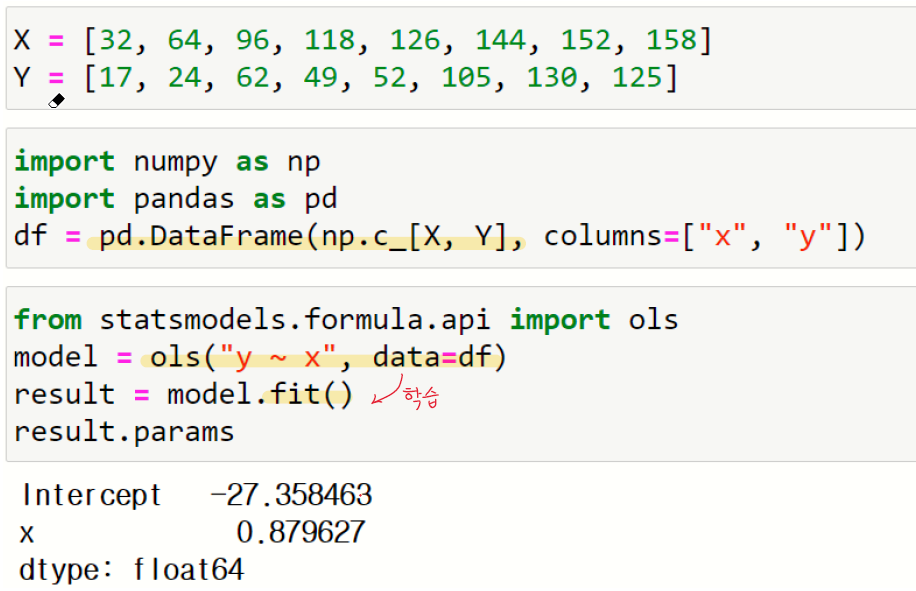
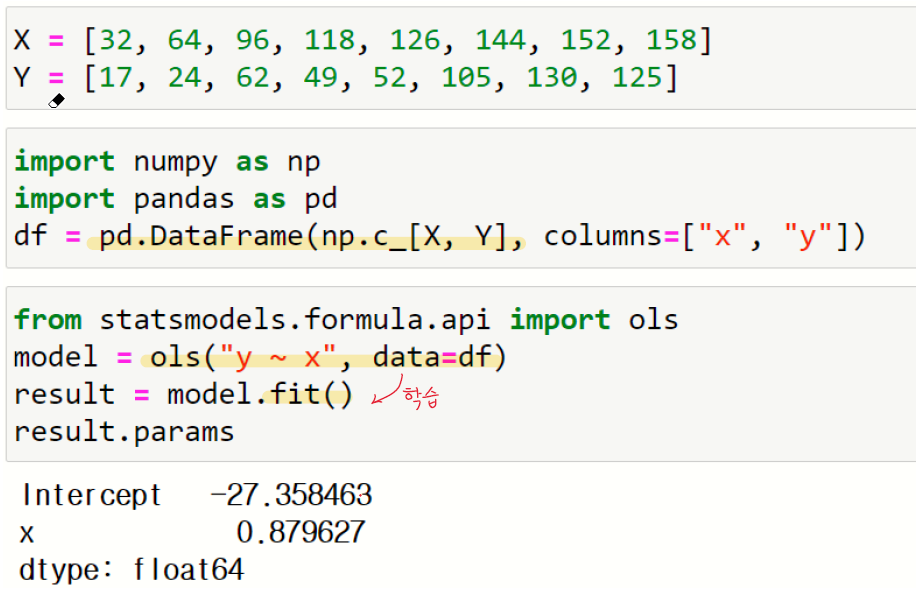
단순 회귀분석은 독립변수가 하나일 경우의 회귀분석이다. y=a*x + b 형식의 수식을 정의하고 a와 b 계수를 구하는 것이 회귀분석이다.
회귀분석을 위해 다양한 방법을 사용할 수 있다.
4.1. 행렬을 이용한 회귀모형 구하기

left sudo inversion 을 이용한 기울기 값 구하기
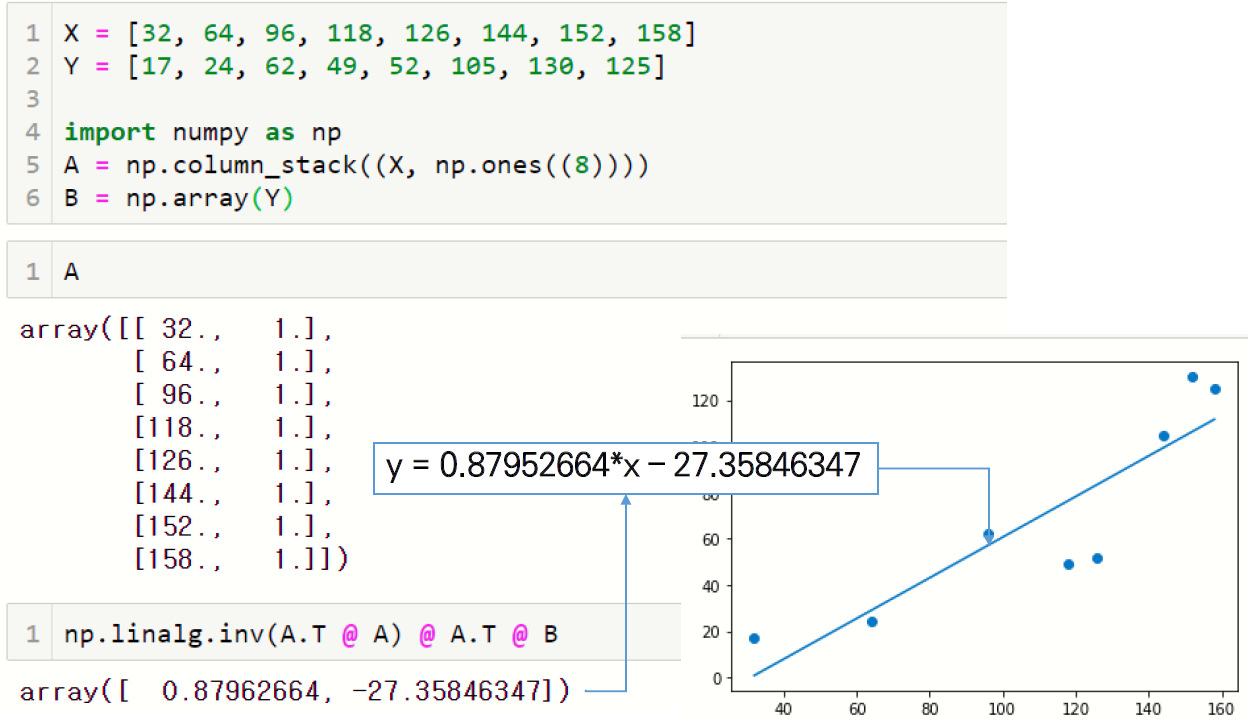
4.2. 회귀모형과 예측
역행렬을 이용해서 회귀식을 구할 수 있지만 scipy 패키지의 linregress() 함수와 numpy 패키지의 polyfit() 함수들을 이용하면 더 쉽게 회귀식을 구할 수 있다.
1) linregress()
linregress()함수는 선형 최소 제곱 회귀식을 계산
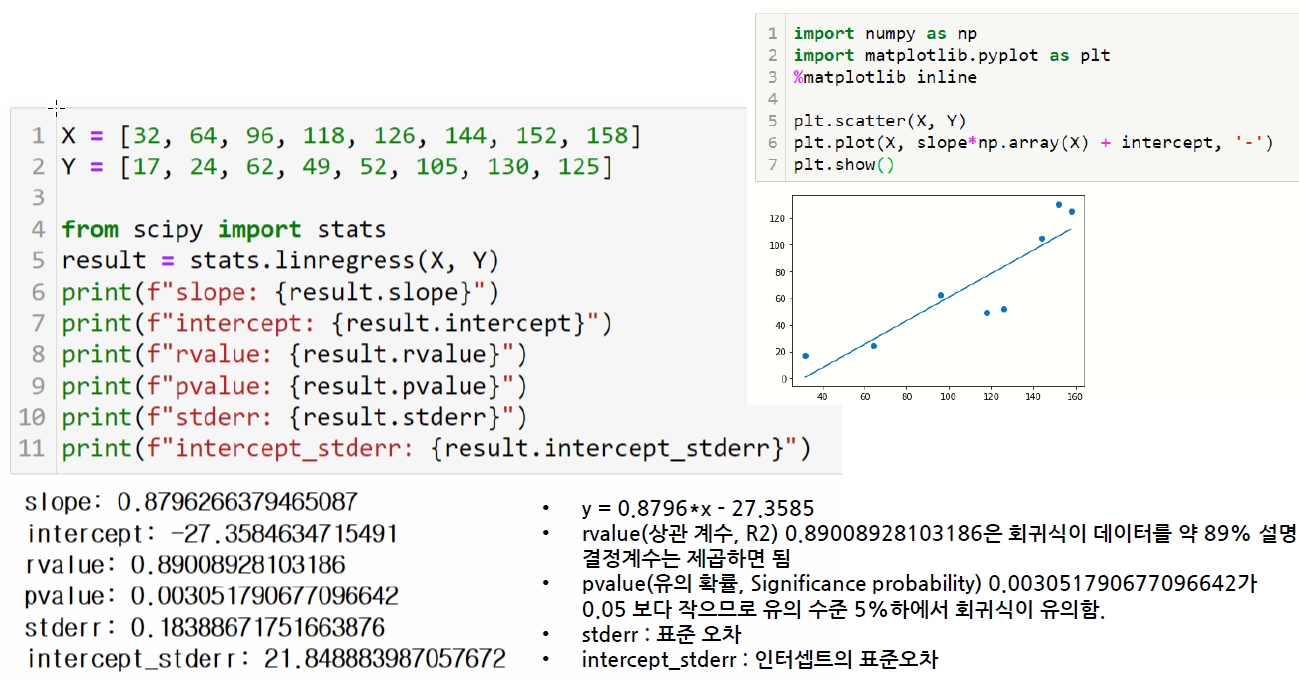
2) polyfit()
numpy의 polyfit() 함수는 최소제곱 다항 회귀식을 계산한다.
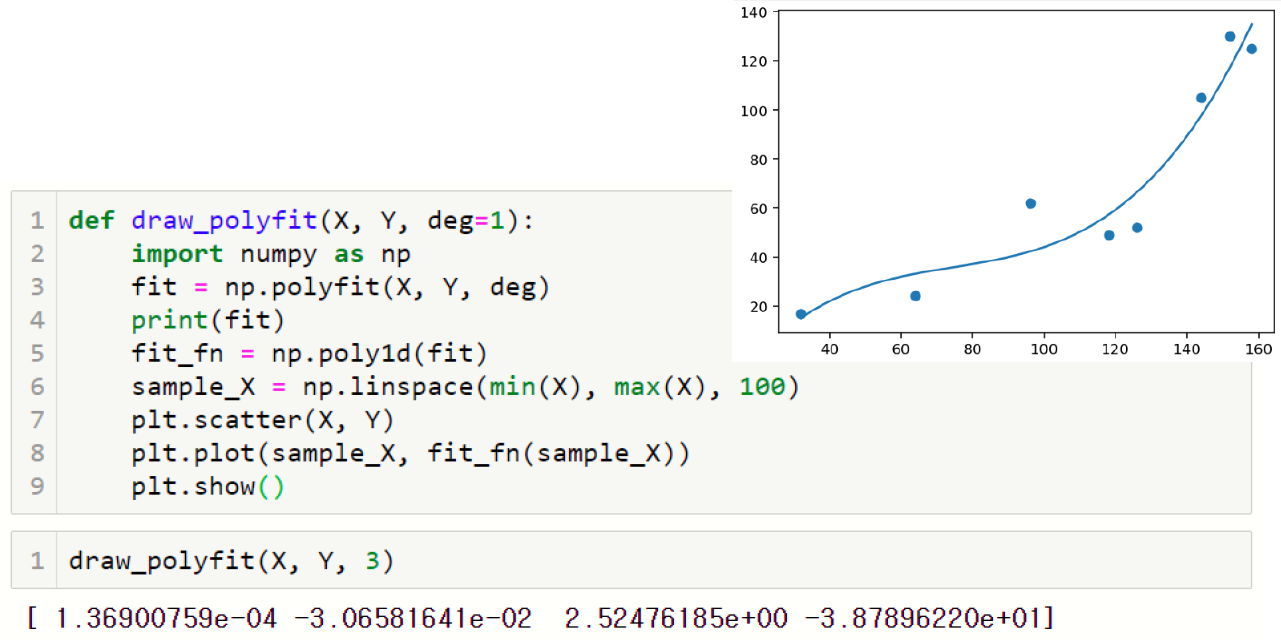
반복되는 코드작성을 줄이기 위해 함수로 만들어줄 수 있다.
def draw_polyfit(X,Y,deg=1):
import numpy as np
fit=np.polyfit(X,Y,deg)
print(fit)
fit_fn=np.poly1d(fit)
sample_X=np.linspace(min(X),max(X),100)
plt.scatter(X,Y)
plt.plot(sample_X, fit_fn(sample_X))
plt.show()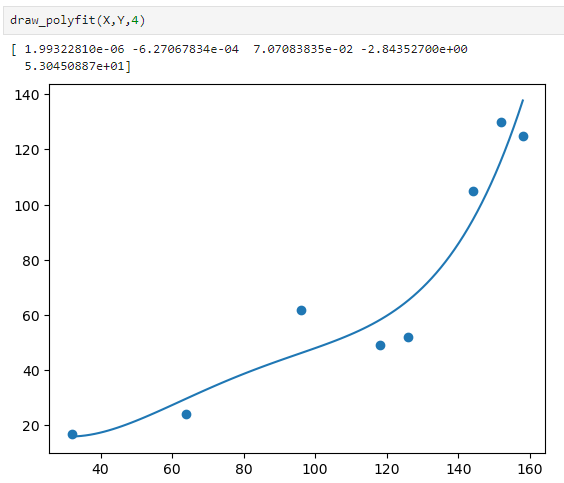
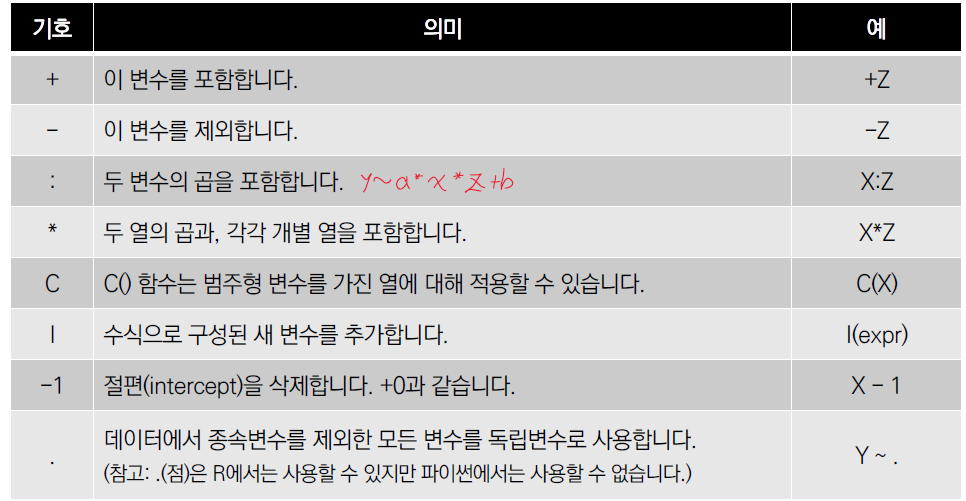
5절. 포뮬러를 이용한 회귀식
선형회귀식을 구하기 위해 formula(포뮬러) 구문을 사용하여 통계 모형의 형식을 지정
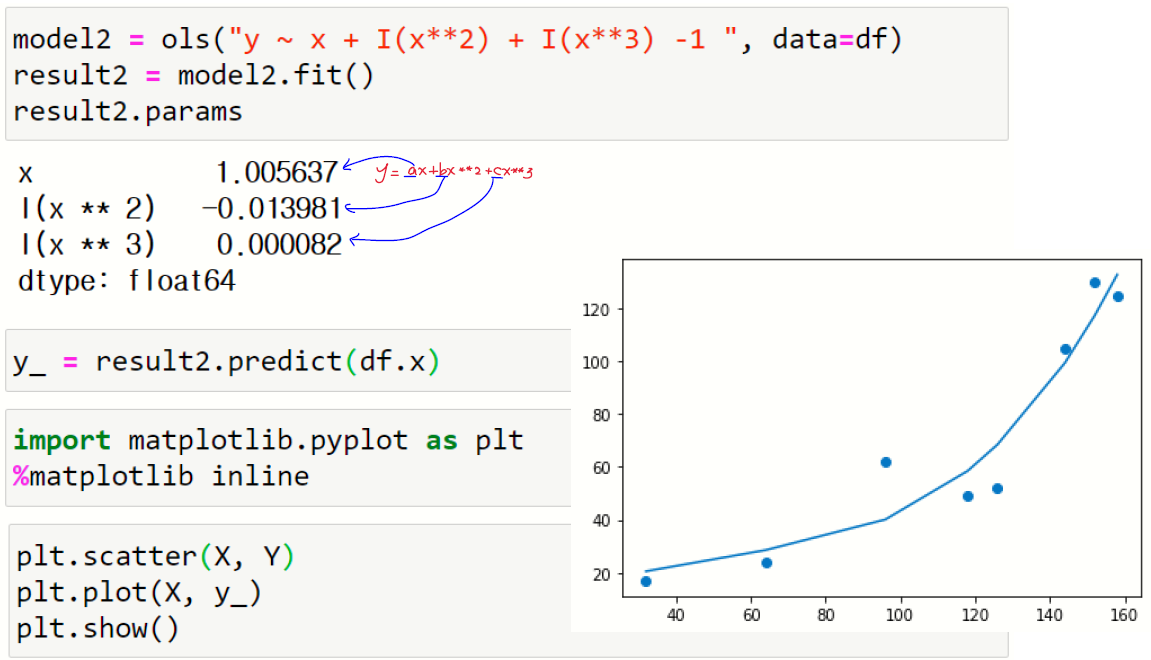
ols() 함수 또는 OLS클래스의 from_formula()를 사용하면 포뮬러를 이용하여 다항 회귀식을 구할 수 있음