[문제 바로가기] https://www.acmicpc.net/problem/20055
📌문제 설명
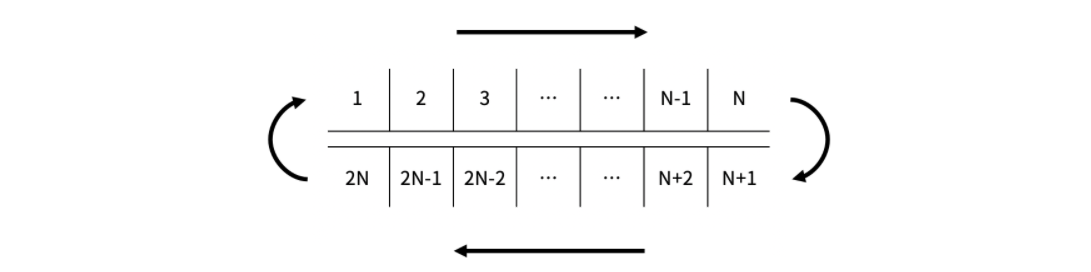
길이가 N인 컨베이어 벨트가 있고, 길이가 2N인 벨트가 이 컨베이어 벨트를 위아래로 감싸며 돌고 있다. 벨트는 길이 1 간격으로 2N개의 칸으로 나뉘어져 있으며, 각 칸에는 아래 그림과 같이 1부터 2N까지의 번호가 매겨져 있다.
벨트가 한 칸 회전하면 1번부터 2N-1번까지의 칸은 다음 번호의 칸이 있는 위치로 이동하고, 2N번 칸은 1번 칸의 위치로 이동한다. i번 칸의 내구도는 Ai이다. 위의 그림에서 1번 칸이 있는 위치를 "올라가는 위치", N번 칸이 있는 위치를 "내려가는 위치"라고 한다.
컨베이어 벨트에 박스 모양 로봇을 하나씩 올리려고 한다. 로봇은 올라가는 위치에만 땅에서 올라가고, 내려가는 위치에서만 땅으로 내려갈 수 있다. 내려가는 위치에 로봇이 있는 경우 로봇은 반드시 땅으로 내려가야 한다. 로봇이 어떤 칸에 올라가거나 이동하면 그 칸의 내구도는 즉시 1만큼 감소한다. 내구도가 0인 칸에는 로봇이 올라갈 수 없다.
로봇은 컨베이어 벨트 위에서 스스로 이동할 수 있다.
컨베이어 벨트를 이용해 로봇들을 건너편으로 옮기려고 한다. 로봇을 옮기는 과정에서는 아래와 같은 일이 순서대로 일어난다.
- 벨트가 한 칸 회전한다.
- 가장 먼저 벨트에 올라간 로봇부터, 벨트가 회전하는 방향으로 한 칸 이동할 수 있다면 이동한다. 만약 이동할 수 없다면 가만히 있는다.
- 로봇이 이동하기 위해서는 이동하려는 칸에 로봇이 없으며, 그 칸의 내구도가 1 이상 남아 있어야 한다.
- 올라가는 위치에 로봇이 없다면 로봇을 하나 올린다.
- 내구도가 0인 칸의 개수가 K개 이상이라면 과정을 종료한다. 그렇지 않다면 1번으로 돌아간다.
종료되었을 때 몇 번째 단계가 진행 중이었는지 구해보자. 가장 처음 수행되는 단계는 1번째 단계이다.
입력
첫째 줄에 N, K가 주어진다. 둘째 줄에는 A1, A2, ..., A2N이 주어진다.출력
몇 번째 단계가 진행 중일때 종료되었는지 출력한다.제한
- 2 ≤ N ≤ 100
- 1 ≤ K ≤ 2N
- 1 ≤ Ai ≤ 1,000
💡 문제 풀이
문제의 단계를 잘 이해하고 그대로 구현하면 되는 시뮬레이션 유형의 문제다.
처음에 문제를 제대로 이해하지 못해서 당황했다. 😂
컨베이어 벨트에서 올라가는/내려가는 부분이 존재한다. 벨트가 한 바퀴씩 순회하면서 올라가는/내려가는 부분의 위치가 바뀌게 되는데, 해당 내용은 자료구조 queue를 이용해서 표현하였다.
로봇 역시 컨베이어 벨트와 함께 움직이므로 컨베이어 벨트 위 로봇의 위치를 표현하기 위해 queue 자료구조를 이용하였다.
문제를 풀면서 queue 자료구조를 한 바퀴 순회할 때 queue.appendleft(queuepop())으로 표현하였는데 queue에 rotate 메소드가 존재하여 횟수만 넣어주면 쉽게 회전을 구현할 수 있었다.
코드는 다음과 같다.
import sys
from collections import deque
N, K = map(int, input().split())
convey = deque(list(map(int, sys.stdin.readline().split())))
robot = deque([0] * N)
answer = 0
while convey.count(0) < K:
convey.rotate(1) # 컨베이어 queue 회전
robot.rotate(1) # 로봇 queue 회전
robot[-1] = 0 # 마지막칸은 항상 내려가는 자리이므로 0
if sum(robot): # 로봇이 존재하면
for idx in range(N-2, -1, -1): # 내려가는 부분 이전의 위치에 존재하는 로봇들을 움직인다.
if robot[idx] and not robot[idx+1] and convey[idx+1]:
convey[idx+1] -= 1
robot[idx+1], robot[idx] = 1, 0
robot[-1] = 0 # 마지막칸은 항상 내려가는 자리이므로 0
if not robot[0] and convey[0]: # 올라가는 자리에 로봇을 올려놓을 수 있으면 로봇을 올린다.
robot[0] = 1
convey[0] -= 1
answer += 1
print(answer)