[문제 바로가기] https://www.acmicpc.net/problem/19238
📌문제 설명
스타트링크가 "스타트 택시"라는 이름의 택시 사업을 시작했다. 스타트 택시는 특이하게도 손님을 도착지로 데려다줄 때마다 연료가 충전되고, 연료가 바닥나면 그 날의 업무가 끝난다.
택시 기사 최백준은 오늘 M명의 승객을 태우는 것이 목표이다. 백준이 활동할 영역은 N×N 크기의 격자로 나타낼 수 있고, 각 칸은 비어 있거나 벽이 놓여 있다. 택시가 빈칸에 있을 때, 상하좌우로 인접한 빈칸 중 하나로 이동할 수 있다. 알고리즘 경력이 많은 백준은 특정 위치로 이동할 때 항상 최단경로로만 이동한다.
M명의 승객은 빈칸 중 하나에 서 있으며, 다른 빈칸 중 하나로 이동하려고 한다. 여러 승객이 같이 탑승하는 경우는 없다. 따라서 백준은 한 승객을 태워 목적지로 이동시키는 일을 M번 반복해야 한다. 각 승객은 스스로 움직이지 않으며, 출발지에서만 택시에 탈 수 있고, 목적지에서만 택시에서 내릴 수 있다.
백준이 태울 승객을 고를 때는 현재 위치에서 최단거리가 가장 짧은 승객을 고른다. 그런 승객이 여러 명이면 그중 행 번호가 가장 작은 승객을, 그런 승객도 여러 명이면 그중 열 번호가 가장 작은 승객을 고른다. 택시와 승객이 같은 위치에 서 있으면 그 승객까지의 최단거리는 0이다. 연료는 한 칸 이동할 때마다 1만큼 소모된다. 한 승객을 목적지로 성공적으로 이동시키면, 그 승객을 태워 이동하면서 소모한 연료 양의 두 배가 충전된다. 이동하는 도중에 연료가 바닥나면 이동에 실패하고, 그 날의 업무가 끝난다. 승객을 목적지로 이동시킨 동시에 연료가 바닥나는 경우는 실패한 것으로 간주하지 않는다.
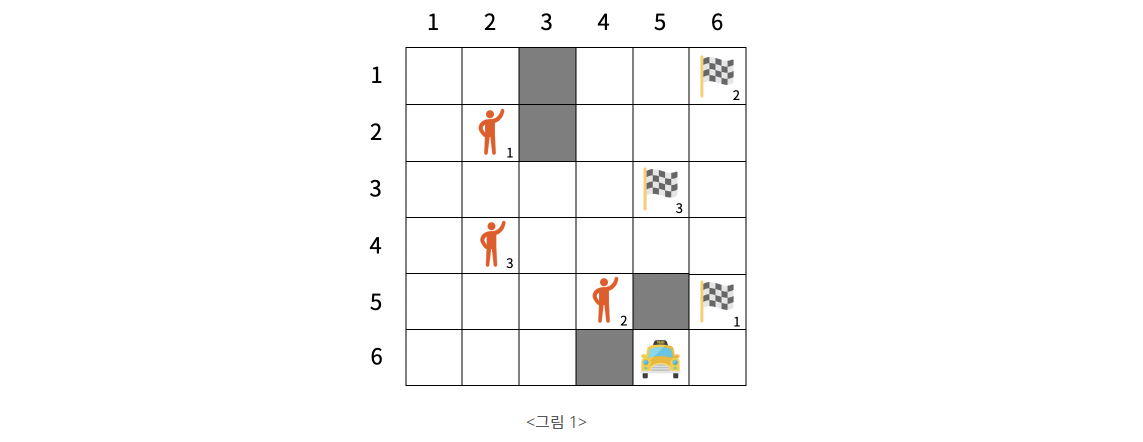
<그림 1>은 택시가 활동할 영역의 지도를 나타내며, 택시와 세 명의 승객의 출발지와 목적지가 표시되어 있다. 택시의 현재 연료 양은 15이다. 현재 택시에서 각 손님까지의 최단거리는 각각 9, 6, 7이므로, 택시는 2번 승객의 출발지로 이동한다.
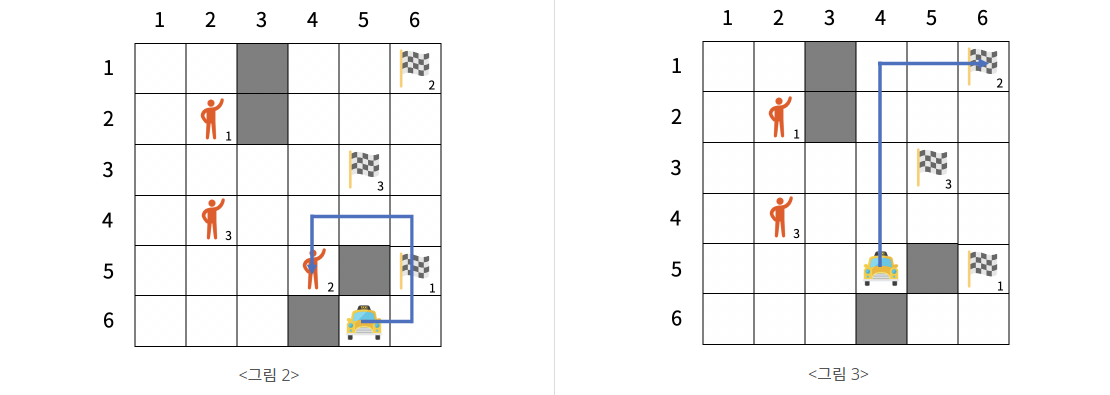
<그림 2>는 택시가 2번 승객의 출발지로 가는 경로를, <그림 3>은 2번 승객의 출발지에서 목적지로 가는 경로를 나타낸다. 목적지로 이동할 때까지 소비한 연료는 6이고, 이동하고 나서 12가 충전되므로 남은 연료의 양은 15이다. 이제 택시에서 각 손님까지의 최단거리는 둘 다 7이므로, 택시는 둘 중 행 번호가 더 작은 1번 승객의 출발지로 이동한다.
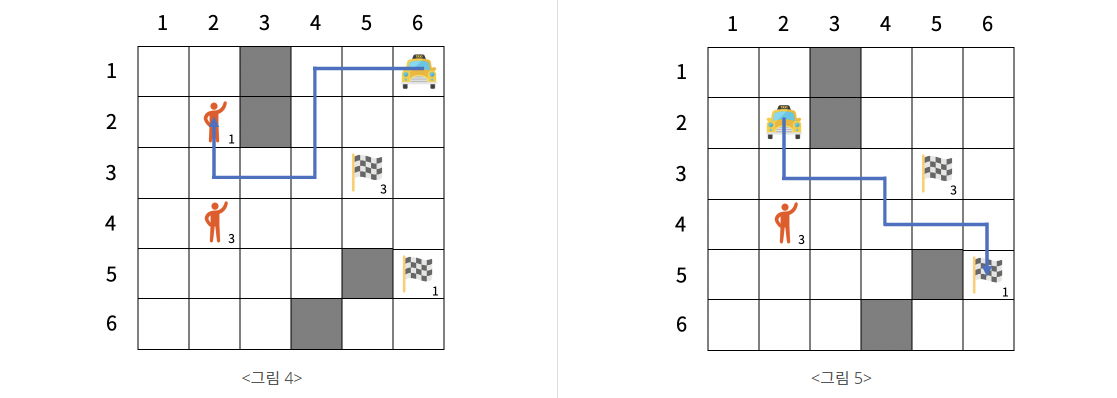
<그림 4>와 <그림 5>는 택시가 1번 승객을 태워 목적지로 이동시키는 경로를 나타낸다. 남은 연료의 양은 15 - 7 - 7 + 7×2 = 15이다.
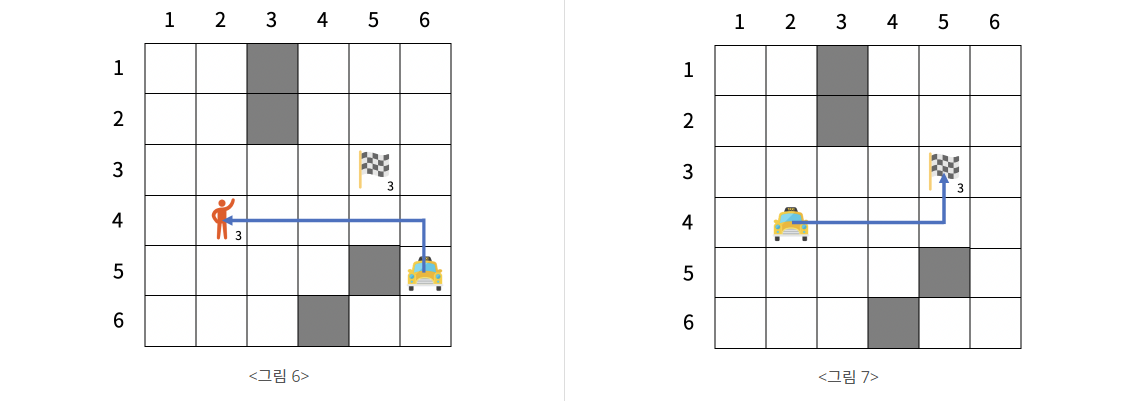
<그림 6>과 <그림 7>은 택시가 3번 승객을 태워 목적지로 이동시키는 경로를 나타낸다. 최종적으로 남은 연료의 양은 15 - 5 - 4 + 4×2 = 14이다.
모든 승객을 성공적으로 데려다줄 수 있는지 알아내고, 데려다줄 수 있을 경우 최종적으로 남는 연료의 양을 출력하는 프로그램을 작성하시오.
입력
첫 줄에 N, M, 그리고 초기 연료의 양이 주어진다. (2 ≤ N ≤ 20, 1 ≤ M ≤ N2, 1 ≤ 초기 연료 ≤ 500,000) 연료는 무한히 많이 담을 수 있기 때문에, 초기 연료의 양을 넘어서 충전될 수도 있다.다음 줄부터 N개의 줄에 걸쳐 백준이 활동할 영역의 지도가 주어진다. 0은 빈칸, 1은 벽을 나타낸다.
다음 줄에는 백준이 운전을 시작하는 칸의 행 번호와 열 번호가 주어진다. 행과 열 번호는 1 이상 N 이하의 자연수이고, 운전을 시작하는 칸은 빈칸이다.
그다음 줄부터 M개의 줄에 걸쳐 각 승객의 출발지의 행과 열 번호, 그리고 목적지의 행과 열 번호가 주어진다. 모든 출발지와 목적지는 빈칸이고, 모든 출발지는 서로 다르며, 각 손님의 출발지와 목적지는 다르다.
출력
모든 손님을 이동시키고 연료를 충전했을 때 남은 연료의 양을 출력한다. 단, 이동 도중에 연료가 바닥나서 다음 출발지나 목적지로 이동할 수 없으면 -1을 출력한다. 모든 손님을 이동시킬 수 없는 경우에도 -1을 출력한다.
💡 문제 풀이
BFS + 시뮬레이션 유형의 문제였다.
벽이 없으면 단순히 행, 열 좌표로 거리를 계산할 수 있었을 텐데 벽이 있기 때문에 BFS를 이용하여 최단 거리를 구하였다.
이후 승객을 태우고 목적지 까지 이동하며 연료를 변동시켜주는 부분은 문제 그대로 구현하면 된다.
문제를 푼 순서는 다음과 같다.
- 택시의 위치를 기준으로 BFS를 이용하여 거리를 구한다.
- 태우지 않은 승객들을 대상으로 가장 가까운 승객을 찾는다.
- 거리가 가까우면 행 값이 작은 승객을 선택한다.
- 행도 같다면 열 값이 작은 승객을 선택한다.
- 남아 있는 연료와 승객과의 거리를 비교한다.
- 만약, 남은 연료 < 승객까지 거리 이면 -1을 출력하고 진행을 멈춘다.
- 만약, 남은 연료 > 승객까지 거리 이면 남은 연료 - 승객까지 거리를 한다.
- 태운 승객 위치를 기준으로 BFS를 이용하여 거리를 구한다.
- 태운 승객의 번호와 동일한 번호의 목적지까지의 거리를 찾는다.
- 만약, 남은 연료 < 목적지까지 거리 이면 -1을 출력하고 진행을 멈춘다.
- 만약, 남은 연료 > 목적지까지 거리 이면 남은 연료 + 목적지까지 거리를 한다.
- 목적지까지 승객을 태워주었으면 해당 승객 번호에 완료 표시를하고, 택시의 행, 열을 최신화한다.
코드는 다음과 같다.
import sys
from copy import deepcopy
from collections import deque
d = [(0, 1), (0, -1), (1, 0), (-1, 0)]
def pick(distance):
man = -1 # 선택한 승객의 번호
now = int(1e9)
for idx in range(M):
if not done[idx]:
r, c = customer[idx][0], customer[idx][1]
if distance[r][c] < now: # 거리가 작으면 갱신
now = distance[r][c]
man = idx
elif distance[r][c] == now: # 거리가 같으면
if r < customer[man][0]: # 행 값이 작은 승객을 선택
man = idx
elif r == customer[man][0]: # 행 값도 같으면
if c < customer[man][1]: # 열 값이 작은 승객을 선택
man = idx
return man
def bfs(tr, tc): # 최단 거리 구하기
queue = deque([(tr, tc)])
distance = deepcopy(origin) # 거리를 표시할 행렬
distance[tr][tc] = 1
while queue:
r, c = queue.popleft()
for idx in range(4):
nr = r + d[idx][0]
nc = c + d[idx][1]
if 0 <= nr < N and 0 <= nc < N:
if not distance[nr][nc]:
queue.append((nr, nc))
distance[nr][nc] = distance[r][c] + 1
return distance
N, M, fuel = map(int, input().split())
origin = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
customer = []
tr, tc = map(int, input().split()) # 택시의 행, 열
tr -= 1; tc -= 1 # 인덱스는 0부터 이므로 1씩 빼주었다.
for _ in range(M):
sr, sc, er, ec = map(int, input().split())
customer.append((sr-1, sc-1, er-1, ec-1)) # 승객의 행, 열 / 목적지의 행, 열
done = [False] * M # 승객 탑승 여부를 알려주는 배열
while done.count(False): # 모든 승객을 이동시키지 않았다면 아래의 내용을 반복
distance = bfs(tr, tc) # 택시 ~ 승객 거리 찾기
man = pick(distance) # 가까운 승객 선택
dist_man = distance[customer[man][0]][customer[man][1]] # 승객까지의 거리
if not dist_man or fuel < dist_man - 1: # 만약 벽으로 인해 갈 수 없거나 남은 연료보다 거리가 더 크면
fuel = -1 # -1을 출력하고 탐색 중지
break
fuel -= (dist_man - 1) # 이동이 가능하면 연료값 최신화
distance = bfs(customer[man][0], customer[man][1]) # 택시(with 승객) ~ 목적지 거리 찾기
dist_goal = distance[customer[man][2]][customer[man][3]] # 목적지 까지 거리
if not dist_goal or fuel < dist_goal - 1: # 이동 가능 여부 확인
fuel = -1
break
fuel += dist_goal - 1 # 연료값 최신화
done[man] = True # 승객 이동 여부 최신화
tr, tc = customer[man][2], customer[man][3] # 택시 위치(행, 열) 최신화
print(fuel)승객을 목적지까지 이동시키는데 두 번의 BFS를 진행하기 때문에, 메모리를 추가로 사용해서 BFS 탐색의 시간 복잡도를 줄일까 했는데 해당 코드로도 충분히 통과가 가능했다. 👍