그래픽스 강의를 보고 있는데 투영 행렬의 유도과정에 대한 설명이 없어 유도를 해볼겸
블로그를 작성합니다.
책은 DIRECTX12 LUNA 책에서 설명이 나와있어 이걸 한 번 정리해보겠습니다.
일단 유도하려는 행렬의 모양은 다음과 같습니다.
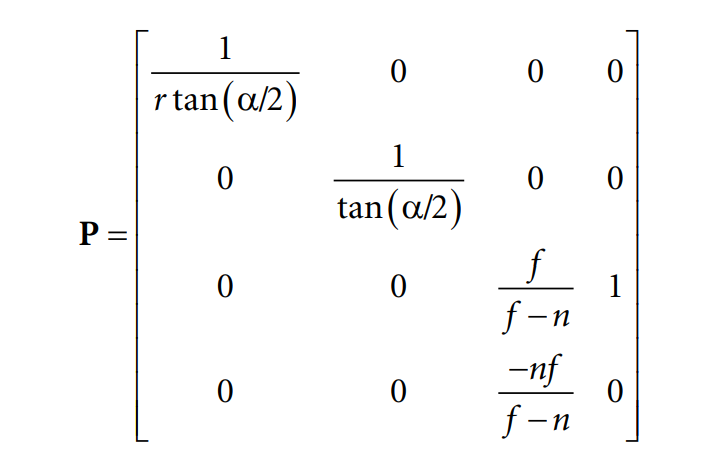
이 행렬을 아래 도식을 통해 유도하는 풀이를 적어보겠습니다.
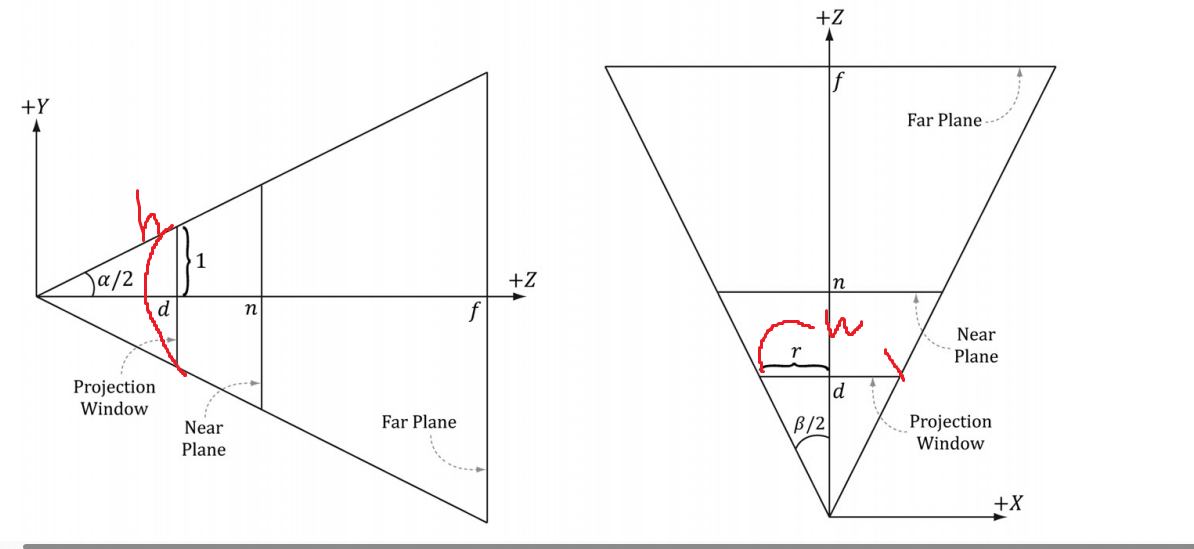
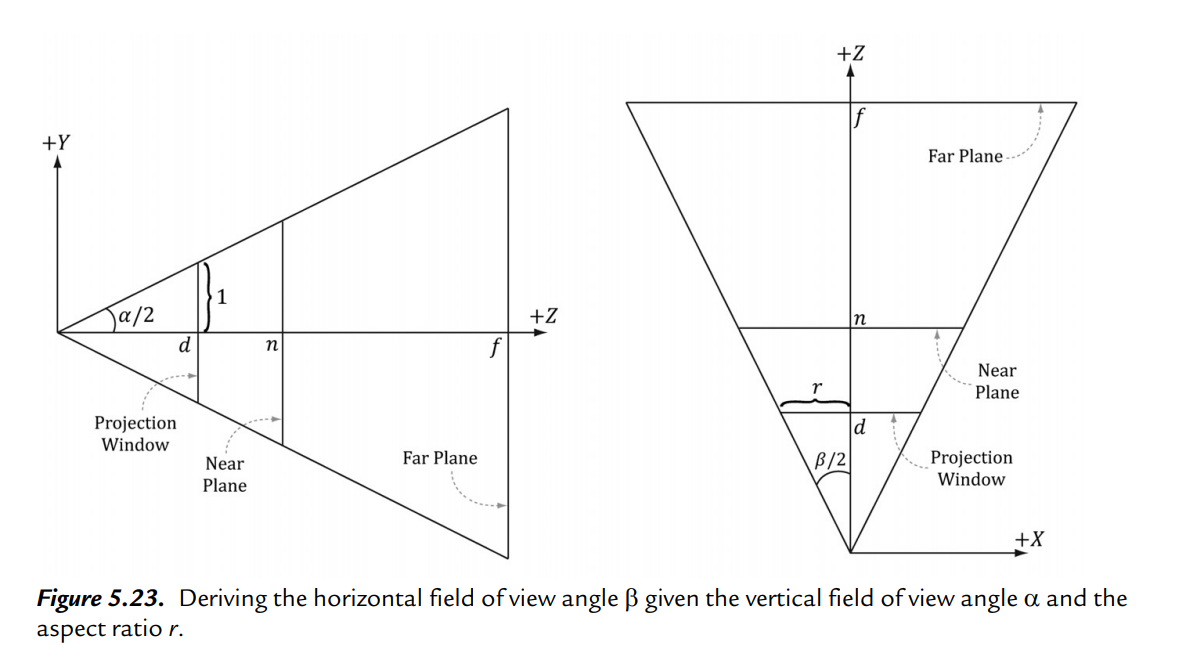
Frustum에서 projection window에서 width가 w이고 height가 h로 표기되어있습니다.
h의 절반이 1이니까 h는 2가 됩니다.
그림의 r은 aspect 종횡비를 말합니다.
따라서 r = w/h -> r = w/2 -> w = 2r로 유도가 됩니다.
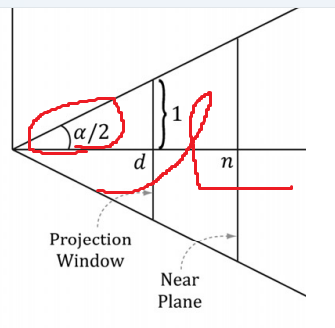
절두체를 옆에서 보았을 때 tan(α/2) = 1/d -> d=cot(α/2) 가 됩니다.(삼각함수) - 2번식
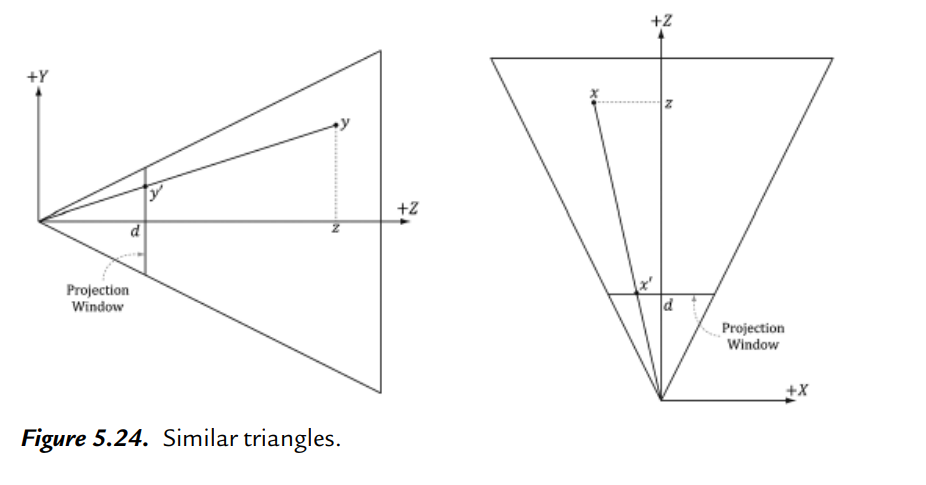
사진의 오른쪽 그림에서 x'/d 의 비율과 x/z의 비율은 같습니다. 따라서 x'/d = x/z 가 됩니다.
2번 식에서 tan(α/2) = 1/d -> d=cot(α/2)였기 때문에
x' = xd/z
x' = x(cot(α/2))/z
x' = x/z(tan(α/2)) 순으로 전개가 됩니다.
y도 마찬가지로 전개되어
y' = y/z(tan(α/2)) 가 됩니다.
이제 projection된 point를 Normalized Device Coordinates로 변환합니다.
왜냐하면 사용자마다 모니터가 다 다른데 이 모니터의 종횡비의 종속성에서 벗어나기 위해서입니다.
ndc 좌표계는 가로 세로가 -1~1로 정규화 되어있는 좌표계입니다.
뷰 스페이스에서 projection 윈도우는 height가 2이고 width가 2r입니다
[-r,r] 을 [-1,1]의 좌표로 변환하면 -1 <= x'/r <= 1 됩니다. (*r은 종횡비 aspect)
y는 변환할 필요가 없기 때문에 -1 <= y' <= 1
z는 n <= z <=f (* n,f는frustum의 near far를 의미) 로 정규화 됩니다.
따라서 아까전의 x' = x(cot(α/2))/z 을 r로 나눠 정규화 해줍니다.
그러면 (*y도 마찬가지)
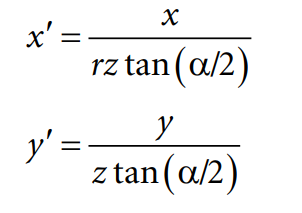
이렇게 정리가 됩니다.
이 수식을 행렬로 정리하면
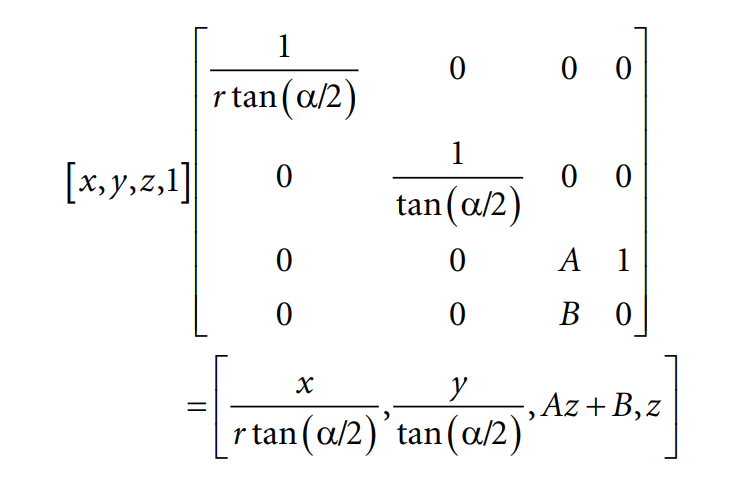
이렇게 정리 할 수 있습니다. 어떤 점 (x,y,z,1)을 투영변환 하는 것이니까 마지막에 1은 directx에서 point는 좌표계 컬럼을 하나 증가시켜서 0이면 벡터 1이면 포인터로 표기하기 때문에 1이라고 적혀있는 것입니다.
A,B는 z값의 정규화를 위한 것입니다. 이건 바로 뒤에 설명마저 하겠습니다.
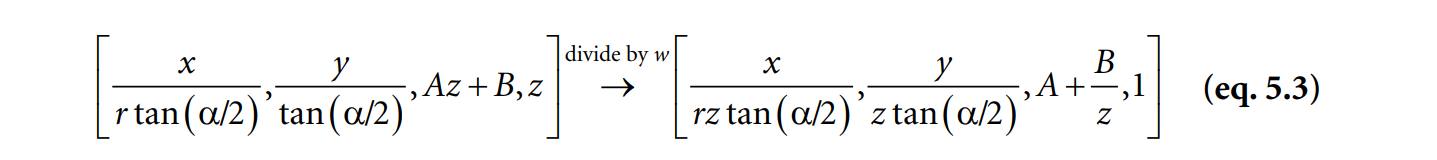
point를 변환하면 위 사진에서 왼쪽과 같은 결과가 나올텐데 전체 좌표를 z로 나누어
homogeneous coordinate로 변환하는 것입니다.
마지막으로 A+B/z의 수식은
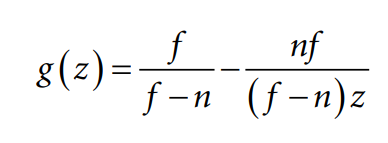
이렇게 됩니다. 수식이 왜 이렇게 되냐는 의문이 잇을것인데 이것은 near와 far를 정규화 시키기 위하여 나오게 된 공식입니다.
위 식을 정리하면 z' = f(z-n)/(f-n)z가 됩니다.
만약 z가 n이면 z'=0이 됩니다.
z가 f면 z'=1이 됩니다. 즉 0~1사이 값으로 정규화가 됩니다.
정리하면 투영행렬은
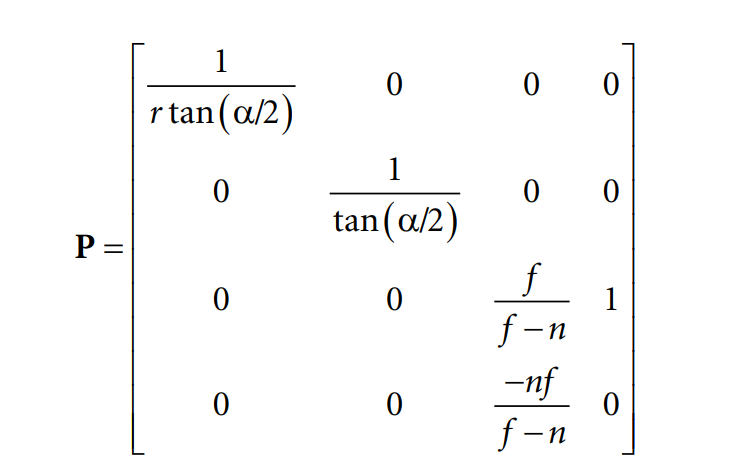
으로 정리가 됨을 알 수 있습니다.
참고
- directx12 LUNA
- 홍정모 선생님의 그래픽스 파트2 : z' = f(z-n)/(f-n)z 설명 참고