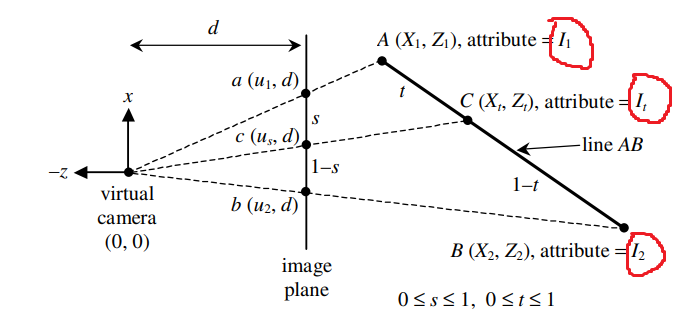
원근 투영 적용해서 물체를 렌더링 시 각 버텍스는 z값이 보간이 되지만
각 보간이 된 정점을 통해 픽셀 값을 보간하려고 하면 왜곡이 발생합니다.
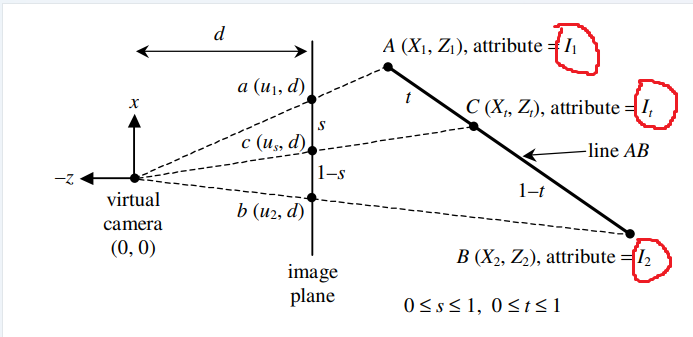
(아래 그림에서 image place의 a,b로 c를 보간하려고하면 왜곡이 발생한다는 이야기)
*보간이라는 것은 데이터가 드문드문 주어질 때 그 사이의 어떤 값을 추론하는 방법을 말합니다.
원근투영의 왜곡을 보정하는 방법을 설명한 논문에서
스크린 좌표계로 보간된 정점과 월드좌표계의 vertex의 z값만을 가지고 스크린 좌표계에 보간이 적용된 픽셀 값을 얻는 방법을 알려줍니다.
풀이 :
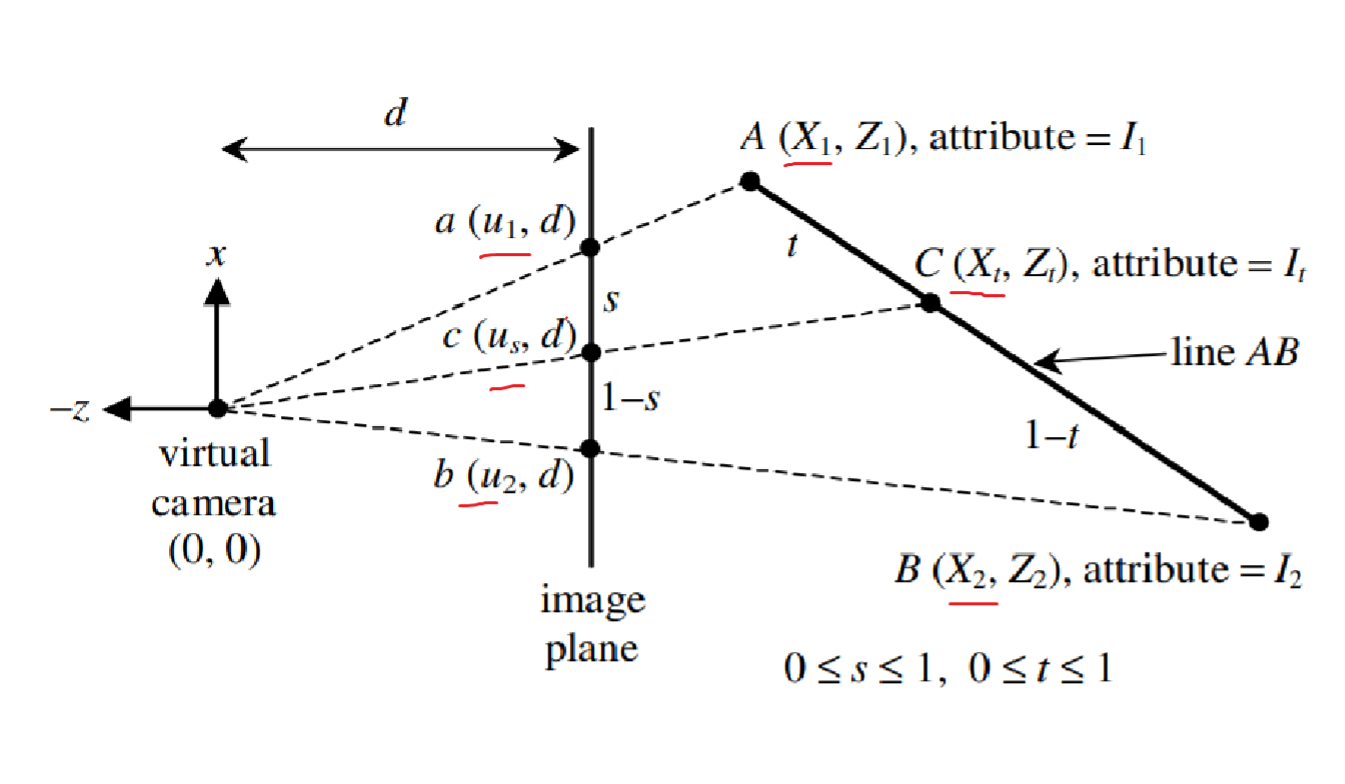
먼저 그림의 It값을 얻기 위해서는 t값을 알아내야 합니다.
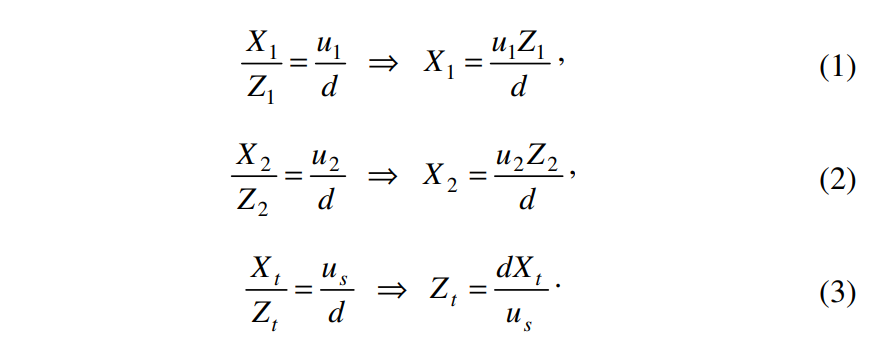
삼각형이 닮은꼴이기 때문에 위의 비례식이 성립합니다. (*1,2,3번식 기억 필요)
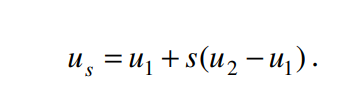
선분위의 한 점은 Affine sum 으로 표현 할 수 있습니다.
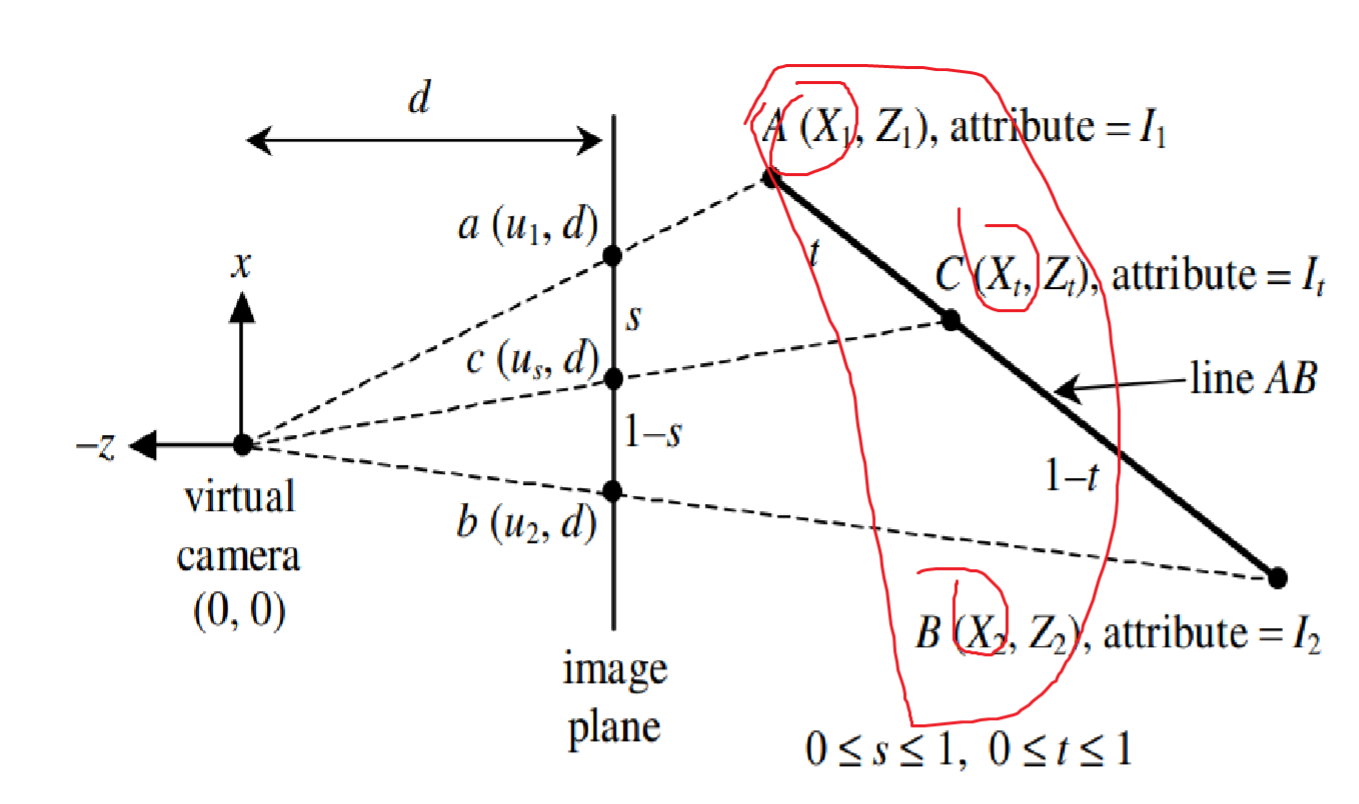
위 세점을 Affine sum을 통해 xt를 보간하면
Xt = X1 + t(X2 - X1)
Zt = Z1 + t(Z2 - Z1)
이 됩니다.
각 내용을 위 3번식에 적용하면
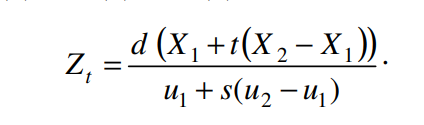
위와 같음을 알 수 있습니다.
위 식에 1,2번 식을 대입하면
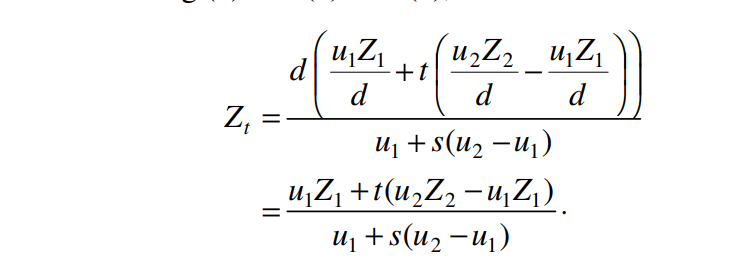
과 같이 전개가 됩니다.
Zt = Z1 + t(Z2 - Z1) 이기 때문에
Z1 + t(Z2 - Z1) = u1Z1 + t(u2Z2 - u1Z1) / (u1 + s(u2 - u1))이 됩니다.
좌항에 t를 남기고 전개하면 (*t 기억 필요)
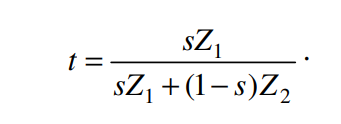
위와 같은 식을 얻을 수 있습니다.
Z1 + t(Z2 - Z1)에 위 t를 대입하면
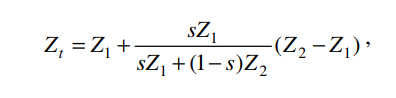
와 같이 나옵니다 이 식을 전개하면

전개 할 수 있습니다.
이제 그림의 I1 I2를 이용해 t값을 추론하면 즉 보간하면 It = I1 + t(I2 - I1)이 됩니다.
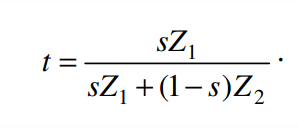
여기에 아까 얻어낸 t값을 대입하면
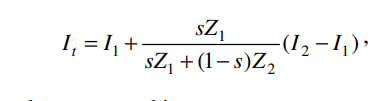
식이 나오고 이를 전개하면
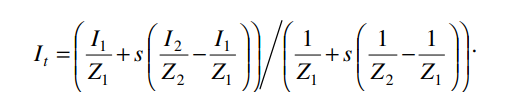
됩니다.
그런데 여기서 분모는 아까 공책에서 전개했던 Zt와 같음을 알 수 있습니다.
즉 최종적으로 월드좌표계의 정점 I1,I2를 보간하여 얻어낸 It의 값은
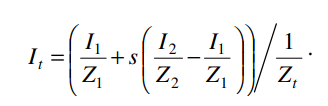
로 정리가 됩니다.
하지만 지금 얻어낸 값은 C (=It)이고 현재 우리가 얻어내야 하는 값은 s입니다.
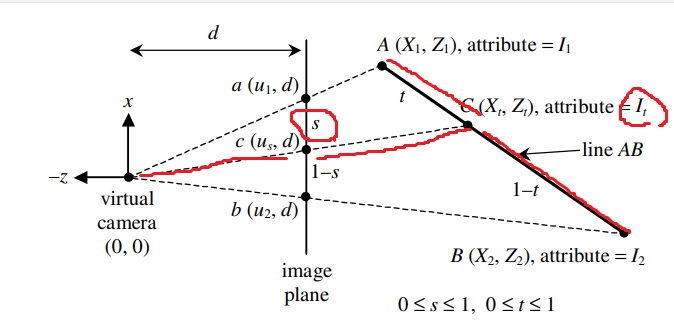
그러면 It, virtual camera를 가지고 linear interpolation을 해서 s를 얻어내야 합니다.
이 후 내용 이해 하려면 다음 문서를 이해해야 됩니다.
논문의 결과인 It를 가지고 다음 해설에서
The first thing we are going to do is substitute the equation for Z (equation 2) on the left-hand side of equation 1.
부터 읽어야 합니다.
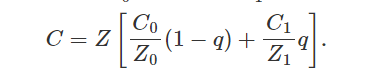
위 수식은 해설의 결과값입니다. 결과값에 따르면 (위 사진의 q가 논문에서 s와 같은 것임)
무게중심좌표계로 계산된 s를 각 버텍트의 z값을 곱해서 보정을 한다고 나옵니다.
이 방식보다 훨씬 간결한 방법을 원근투영에서 픽셀의 보간 (2)에서 작성하겠습니다.
출처