
💡문제
[Gold V] 등차수열과 쿼리 - 23888
성능 요약
메모리: 324788 KB, 시간: 1360 ms
🤔접근법
범위 체크 및 시간복잡도 예상
- 1 ≤ ≤ , 0 ≤ ≤
- 1 ≤ ≤
- 1 ≤ ≤ ≤
- 완탐은 힘들듯 하다.
- 또는 이어야 한다.
풀이법
1 : 번째 항부터 번째 항까지의 합 → 등차수열 합공식
등차 수열의 합공식을 이용하면 상수 시간으로 구할 수 있을 것이라고 생각했다.
등차수열 합공식 : 항의 개수 * (첫째항 + 끝항) / 2
항의 개수가 n개인 등차 수열의 첫째항을 a, 끝항을 , 공차 d
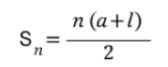
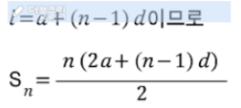
번째 항부터 번째 항까지의 합은 하면 될 듯하다.
2 : 번째 항부터 번째 항까지의 최대 공약수 → 초항과 공차의 최대 공약수
문제는 이게 문젠데 ..
쿼리가 q개 최대 개나 주어지기 때문에 번째 항부터 번째 항까지 (최대 공약수 , 다음항) 해가지고 마지막 항까지 최대공약수를 구하기엔 시간이 부족하다.
그래서 약수부터 다시 집고 넘어가보자. ⚡유클리드호제법⚡
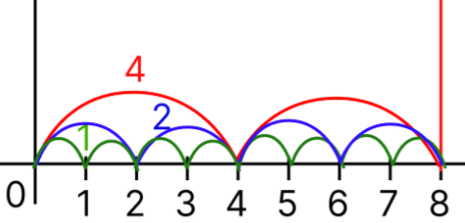
나는 0부터 균일하게 점프해서 도착할 수 있는 수를 약수 라고 정의해보았다.
- 4칸씩 점프해 8에 도착할 수 있으니 4는 8의 약수이다.
- 2칸씩 점프해 8에 도착할 수 있으니 4는 8의 약수이다.
- 1칸씩 점프해 8에 도착할 수 있으니 4는 8의 약수이다.
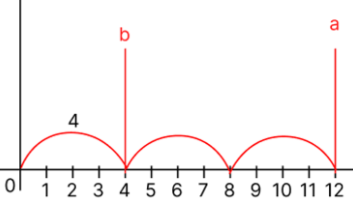
그렇다면 a 도 도착할 수 있고 b에도 도착할 수 있으면 a 와 b의 공약수 이다.
- 4칸씩 점프해서 4에도 도착할 수 있고 12에도 도착할 수 있으니 4는 4와 12의 공약수 이다.
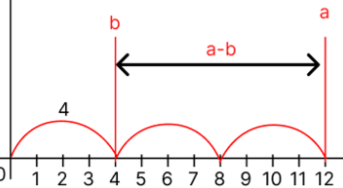
그렇다면 a와 b의 공약수는 a-b의 약수이기도 하다.
- 4와 12의 공약수(4)는 8의 약수(4)이기도 하다.
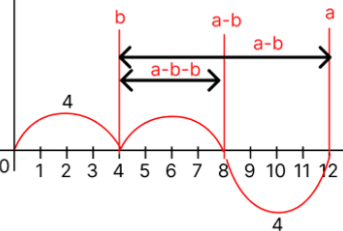
a에서 b를 한번더 빼게 되면 다음과 같이 그릴 수 있다.
여기서 한번 더 빼게 되면 a == b == 4가 되고 a-b ==0이 된다.
이렇게 되었을 때 a의 값이 최대 공약수가 이다.
즉 a에서 b를 뺄 수 있을 때 까지 반복해서 뺀 후 점프하는 수와 동일해 진다면(a-b ==0이라면) 남는 수가 최대 공약수 임을 알 수 있다.
여기서 뺄 수 있을 때까지 반복해서 빼는 이 과정이 gcd 에서 a%b 해주는 모듈러 연산 과정이다.
위 예시에서는 두번 빼는 것이 가능한 경우이다.
다른 예시로 a = 14, b = 6 인 경우를 생각해보자
a 에서 b를 가능할때까지 최대한 반복해서 빼보자.
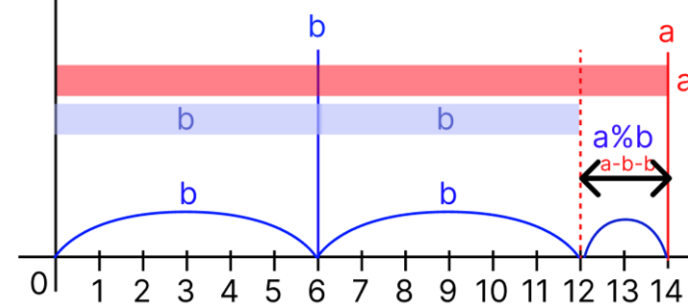
14 - 6 = 8 (a -b)
8 - 6 = 2 (a -b -b)
이렇게 b를 연속해서 가능할때까지 빼는 과정이 a % b 와 동일하다는 것을 말하고 싶었다.
그렇다면 a-b == 0 즉, a %b == 0 이 될때 까지 a = b 로, b = a%b 로 삽입하여 생각해보자.
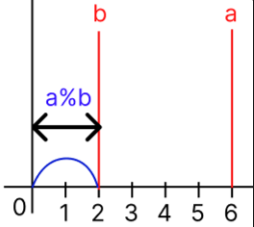
b = 6 이었는데 b값을 a에 넣고, b = a%b 값을 넣어 계산해보면
a = 6, b= 2 가 되며 , a%b == 0이 되어진다.
이때 b의 값이 최대 공약수 이다.
위는 유클리드 호제법일 이해한 방법이며 이의 시간복잡도는 이다.
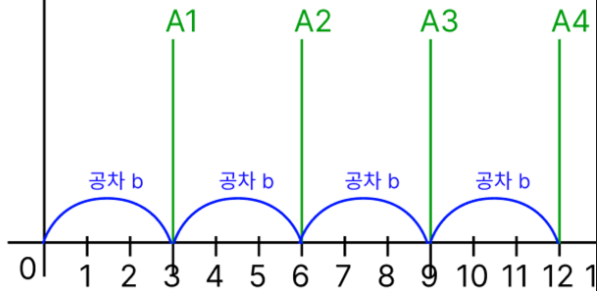
그렇다면 첫번째 항이 0일때 A1, A2, A3, A4는 모두 3이 점프해서 올 수 있으니 동일한 공약수를 가진다. (접힌 글 참고)
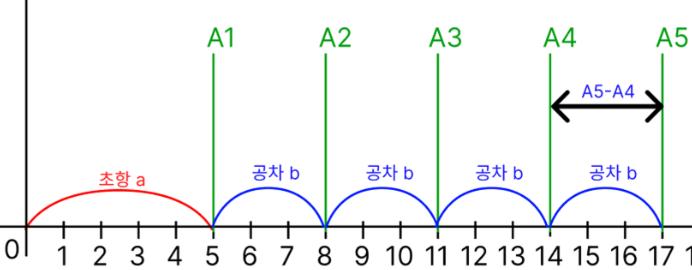
이때 초항을 넣게 되면 0부터 각 A1 ~ A5까지 모두 도달할 수 있는 가장 큰 점프의 크기를 찾아야한다. (접힌 글 참고)
이때 A4, A5의 공약수는 A5-A4의 약수이므로 초항과 공차사이의 최대 공약수를 구하면 된다.
➡️ 해당 풀이법의 시간 복잡도 : 이다
🏆RESULT
🤯틀렸습니다 (%1)
주어진 범위의 과 이 같을 때는 로 최대 공약수도 동일하다.
그걸 조건을 걸어주지 않아서 처음부터 틀렸다.
🤯10점 (%34)
범위 문제였다.
지난번에도 지지난번에도 타입 범위를 제대로 확인하지 않아서 틀렸는데 또 똑같은 문제였다.
초항이 십만이고 공차가 십만이면 int 범위를 넘어갈텐데 당연한 걸 틀렸다 ㅠ
🤯30점 (%67)
출력문제였다.
StringBuilder를 사용하자… T_T
😎 100점 ✅
그래도 초반에 코드 짜기 전 생각한 시간복잡도와 로직은 맞게 판단하였다.
👩💻 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main_23888 {
static long a;
static long d;
static long q;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
a = Long.parseLong(st.nextToken());
d = Long.parseLong(st.nextToken());
q = Long.parseLong(br.readLine());
for (long p = 0; p < q; p++) {
st = new StringTokenizer(br.readLine());
long check = Long.parseLong(st.nextToken());
long l = Long.parseLong(st.nextToken());
long r = Long.parseLong(st.nextToken());
if(check == 1){
sb.append(sequenceSum(r) - sequenceSum(l-1)+"\n");
}else{
if(l == r){
sb.append((a + (l-1)*d)+"\n");
}else{
sb.append(gcd(Math.max(a, d), Math.min(a, d))+"\n");
}
}
}
System.out.println(sb.toString());
}
private static long gcd(long a, long b) {
if(b == 0) return a;
return gcd(b, a%b);
}
private static long sequenceSum(long n) {
return (n * (2*a + (n-1)*d))/2;
}
}