
💡문제
[Gold IV] 직사각형과 쿼리 - 14846
성능 요약
메모리: 88976 KB, 시간: 576 ms
🤔접근법
범위 체크 및 시간복잡도 예상
- 1 ≤ N ≤ 300
- 1 ≤ Q ≤ 100,000
- 이하여야 한다.
풀이법
❌ 접근 방법. 완탐
- (x1, y1) ~ (x2, y2) 를 순회하며 (x, y) 정수를 이미 사용했다면 넘어가고 사용하지 않았다면 체크하고 넘어가기 →
➡️ 해당 풀이법의 시간 복잡도 :
당연히 시간복잡도 초과
⭕ 접근 방법. 누적합
(1, 1) ~ (x ,y)까지의 1 ~10까지 사용개수를 누적하여 저장하는 3차원 배열을 만든다.
- (x, y)를 입력 받으면서 누적 사용 개수 합 배열을 만든다 →
아래 사진 참고
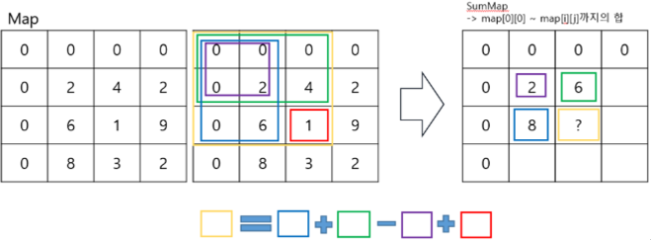
-
쿼리를 돌면서 →
-
구간 사용개수의 합을 구한다. →
아래사진 참고
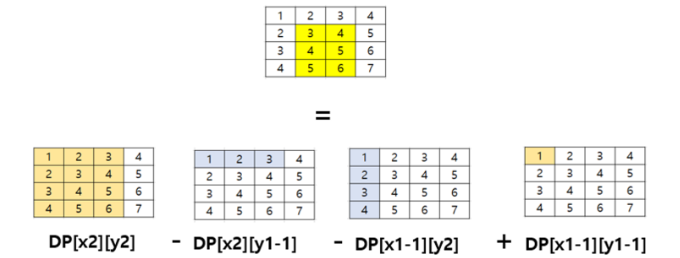
-
사용개수가 1 이상인 정수의 개수를 구한다.
-
➡️ 해당 풀이법의 시간 복잡도 :
🤯FAIL
답을 봐서 문제를 푼 경우
- 해결이 되지 않은 부분 : 삼차원을 이용해야한다는 것까지는 접근했으나 숫자의 개수를 누적할 생각은 못하고 boolean으로 가지고 있는지 없는지만 판별하려 했었다.
- 정답의 로직은 ?
숫자의 개수를 누적하여 구간에 정수마다 몇개를 가지고 있는지 확인할 수 있었다.
😎SUCCESS
StringBuilder를 사용하여 출력한 결과와 사용하지 않고 출력한 결과의 차이이다.
쿼리문제는 무조건 StringBuilder를 사용하자.

👩💻 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main_14846 {
static int N; // 격자의 크기
static int[][][] sum; // 각 격자에 숫자가 등장한 빈도수를 누적한 배열
static int Q; // 질의의 개수
static int x1, x2, y1, y2; // 질의의 좌표 범위
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
sum = new int[N + 1][N + 1][11];
// 격자에 숫자 등장 빈도수를 누적하여 저장
for (int i = 1; i <= N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
int n = Integer.parseInt(st.nextToken());
for (int k = 1; k <= 10; k++) {
sum[i][j][k] = sum[i - 1][j][k] + sum[i][j - 1][k] - sum[i - 1][j - 1][k];
}
sum[i][j][n]++;
}
}
Q = Integer.parseInt(br.readLine());
for (int q = 0; q < Q; q++) {
StringTokenizer st = new StringTokenizer(br.readLine());
x1 = Integer.parseInt(st.nextToken());
y1 = Integer.parseInt(st.nextToken());
x2 = Integer.parseInt(st.nextToken());
y2 = Integer.parseInt(st.nextToken());
sb.append(countNumber(x1, y1, x2, y2)).append("\n");
}
System.out.println(sb.toString());
}
// 질의 범위 내에서 등장한 숫자의 개수를 세는 메서드
private static int countNumber(int x1, int y1, int x2, int y2) {
int[] usedNumber = new int[11];
for (int k = 1; k <= 10; k++) {
usedNumber[k] = sum[x2][y2][k] - sum[x1 - 1][y2][k] - sum[x2][y1 - 1][k] + sum[x1 - 1][y1 - 1][k];
}
int cnt = 0;
for (int i = 1; i <= 10; i++) {
if (usedNumber[i] > 0) {
cnt++;
}
}
return cnt;
}
}