[백준 Java] 1749번 점수따먹기

💡문제

[Gold IV] 점수따먹기 - 1749

문제 링크

성능 요약

메모리: 19256 KB, 시간: 892 ms

---

🤔접근법

범위 체크 및 시간복잡도 예상

• 1 ≤ N ≤ 200, 1 ≤ M ≤ 200
• $O((NM)^2)$이하여야 한다.

풀이법

❌ 접근 방법. 완탐

1. (x1, y1) ~ (x2, y2) 를 순회하며 (x, y) 정수를 이미 사용했다면 넘어가고 사용하지 않았다면 체크하고 넘어가기 → $O(N^2)$

➡️ 해당 풀이법의 시간 복잡도 : $O(N^2Q)$

당연히 시간복잡도 초과

⭕ 접근 방법. 누적합

(1, 1) ~ (x ,y)까지의 누적합을 구한 후 구간에서 최대를 찾는다.

1. (x, y)를 입력 받으면서 누적 합을 저장한다.→ $O(N^2)$

   아래 사진 참고
   

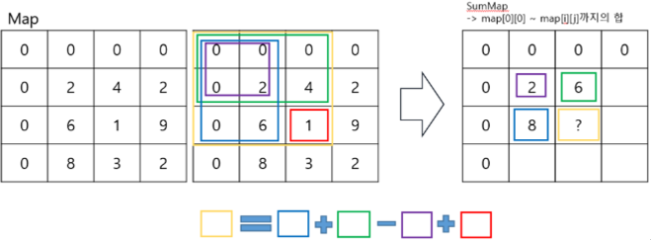
2. 만들 수 있는 구간을 모두 탑색하며 최대 값을 찾는다. → $O((NM)^2)$

   구간 합은 아래와 같이 구할 수 있다.

   matrixSum[endR][endC] - matrixSum[startR - 1][endC] - matrixSum[endR][startC - 1] + matrixSum[startR - 1][startC - 1]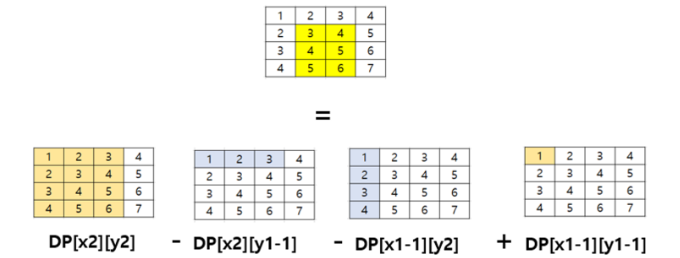

   

➡️ 해당 풀이법의 시간 복잡도 : $O((NM)^2)$

---

🤯FAIL

아직 해결하지 못한 문제 …

• 백준 연속합 문제
  • 위 문제는 구간의 합이 최대가 될때 그 최대값을 출력하는 문제이다. 단 , 배열이 1차원
  • 위 문제의 풀이는 두가지가 있다.
    • 첫번째는 누적합을 구한 후 가능한 모든 구간을 탐색하며 최대를 구하는 방법
    • 두번째는 현재까지 구한 최대에서 현재 값을 더한 다음 최대가 된다면 현재 위치에 최대값을 저장하는 방법, 즉 i라는 인덱스를 포함하여 만들수 있는 구간에서 가장 최대가 되는 값을 인덱스 i에 저장하는 방식이다.
• 연속합 문제의 두번째 풀이를 사용해서 4중 for문으로 모든 구간을 탐색하지 않고 최대를 저장하는 누적배열을 만들어 풀어보려고 하였으나 해결하지 못하였다 흑흑

😎SUCCESS

---

👩‍💻 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    static int N;             // 행의 개수
    static int M;             // 열의 개수
    static int matrix[][];    // 입력으로 주어지는 행렬
    static int matrixSum[][]; // 행렬의 누적 합을 저장하는 배열
    static int max = Integer.MIN_VALUE; // 최댓값을 저장하는 변수

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());

        matrix = new int[N + 1][M + 1];
        for (int i = 1; i <= N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 1; j <= M; j++) {
                matrix[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        matrixSum = new int[N + 1][M + 1];
        // 행렬의 누적 합 계산
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= M; j++) {
                matrixSum[i][j] = matrixSum[i][j - 1] + matrixSum[i - 1][j] + matrix[i][j] - matrixSum[i - 1][j - 1];
            }
        }

        // 모든 부분 행렬의 합 중 최댓값 찾기
        for (int startR = 1; startR <= N; startR++) {
            for (int startC = 1; startC <= M; startC++) {
                for (int endR = startR; endR <= N; endR++) {
                    for (int endC = startC; endC <= M; endC++) {
                        max = Math.max(max, matrixSum[endR][endC] - matrixSum[startR - 1][endC] - matrixSum[endR][startC - 1] + matrixSum[startR - 1][startC - 1]);
                    }
                }
            }
        }
        System.out.println(max);
    }
}