[빅데이터/확률]

💡 집합

• set: mutable 자료형, {} 기호
• frozenset: 내용 변경할 수 없는 immutable 자료형

A = set([1, 2, 3, 3, 2])  # 중복된 자료는 없어진다.
# A는 {1, 2, 3}

B = frozenset(['H', 'T'])
# B는 frozenset({'H', 'T'})

집합의 크기

• len(): 원소의 갯수

len(A), len(B)

합집합과 교집합

• union, intersection 메서드 혹은 |, & 연산자

A1.union(A2)
A1 | A2

A3.intersection(A4)
A4 & A3

전체집합, 부분집합, 여집합

• issubset() 메소드 or <= 연산자

A3.issubset(A1)  #A3이 A1의 부분집합이면 True 리턴
A3 <= A1

A3 <= A3  # 모든 집합은 자기 자신의 부분집합이다.
A3 < A3  # 모든 집합은 자기 자신의 진부분집합(자기 자신을 제외한 부분집합)이 아니다

A = frozenset([])
B = frozenset(['H'])
C = frozenset(['T'])
D = frozenset(['H', 'T'])
set([A, B, C, D])  # {frozenset(), frozenset({'H'}), frozenset({'T'}), frozenset({'H', 'T'})}

차집합과 여집합

• difference() method or - 연산자

A1.difference(A2)
A1 - A2

공집합

empty_set = set([])
empty_set
# set()

empty_set.union(A1) 
# [, 2, 3, 4}

💡 확률

특정 위치에 점 찍기

x = 1
y = 2
plt.scatter(x,y)  #(1, 2)에 점 찍힘.

확률분포 함수

• 어떤 사건에 어느 정도의 확률이 할당되었는지 묘사한 정보
• 확률질량 함수: 유한 개의 사건이 존재하는 경우 각 단순사건에 대한 확률만 정의하는 함수 (0과 양의 정수(자연수)로 표현)
• 누적분포함수 : 표본 수가 무한하고 모든 표본에 대해 표본 하나만을 가진 사건의 확률이 동일하다면, 표본 하나에 대한 사건의 확률은 언제나 0 (주어진 확률 변수가 특정 값보다 작거나 같은 확률)
• 확률밀도 함수 : 사건 결과값들(빈도)의 밀집 정도를, 확률로 나타낸 함수

기본적으로 plot 그리기

• plot( y 축 데이터, 옵션)
• plot( x 축 데이터, y 축 데이터, 옵션)

#한글 폰트 설정
from matplotlib import font_manager, rc
import matplotlib.pyplot as plt

font_location = "c:/Windows/fonts/malgun.ttf"
font_name = font_manager.FontProperties(fname=font_location).get_name()
rc('font', family=font_name)

plt.plot([1,2,3,4])  #y축 데이터
plt.xlabel('x축 한글표시')
plt.show()

plt.figure(figsize=(10, 6))          # 플롯 사이즈 지정
plt.plot(x, y1, color="red")         # 선을 빨강색으로 지정하여 plot 작성          
plt.xlabel("x")                      # x축 레이블 지정
plt.ylabel("y")                      # y축 레이블 지정
plt.grid()                           # 플롯에 격자 보이기
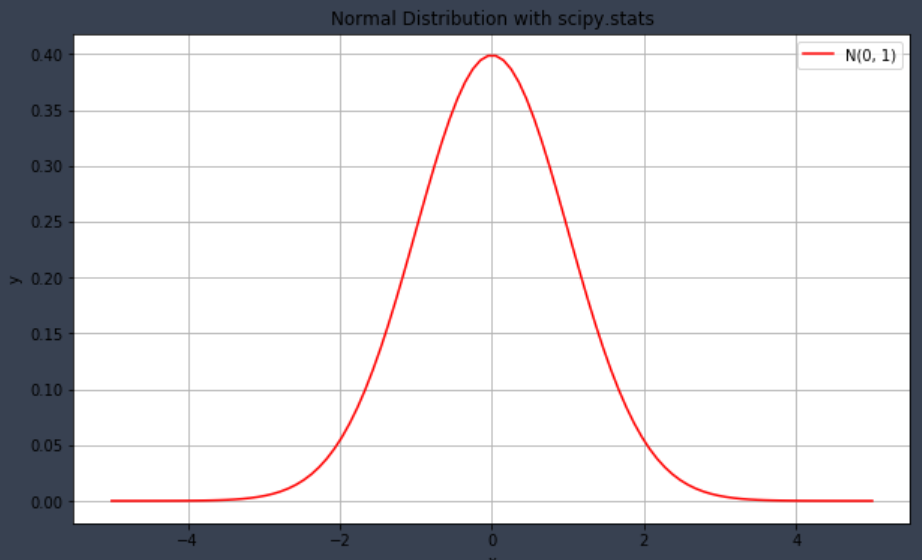
plt.title("Normal Distribution with scipy.stats")     # 타이틀 표시
plt.legend(["N(0, 1)"])              # 범례 표시
plt.show() 

확률질량 함수

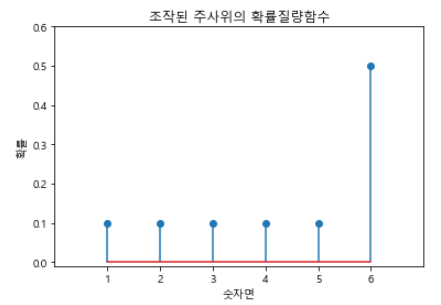
# 확률질량함수

import numpy as np

x = np.arange(1, 7)  #1부터 6까지 순서대로 반환
y = np.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.5])  #각 사건의 확률값
plt.stem(x, y)    #x는 좌표값, y는 x에 대응하는 y값

plt.title("조작된 주사위의 확률질량함수")
plt.xlabel("숫자면")
plt.ylabel("확률")
plt.xlim(0, 7)  #x축 범위 지정
plt.ylim(-0.01, 0.6)  #y축 범위 지정

plt.xticks(np.arange(6) + 1)  #x축에 눈금 표시 (1, 2, 3, ...6)
plt.show()

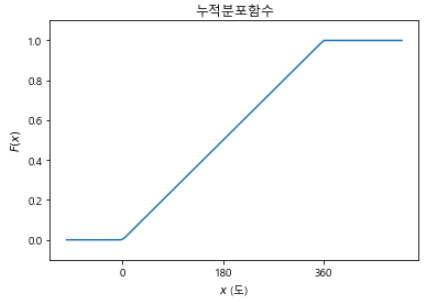
누적분포 함수

t = np.linspace(-100, 500, 100)  # -100부터 500까지 100개의 요소로 만들어라
F = t / 360   # 누적분포함수
F[t < 0] = 0
F[t > 360] = 1

plt.plot(t, F)
plt.ylim(-0.1, 1.1)  #y축 범위 지정
plt.xticks([0, 180, 360])  #x축에 눈금 표시

plt.title("누적분포함수")
plt.xlabel("$x$ (도)")
plt.ylabel("$F(x)$")

plt.show()

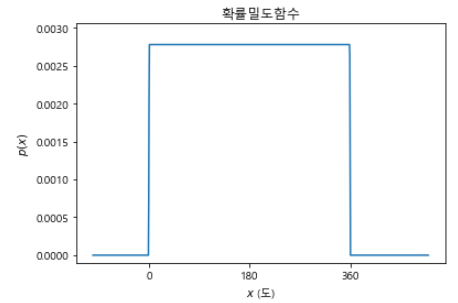
확률밀도 함수

t = np.linspace(-100, 500, 1000)  # -100부터 500까지 100개의 요소로 만들어라
F = t / 360
F[t < 0] = 0
F[t > 360] = 1
p = np.gradient(F, 600/1000)  # 수치미분

plt.plot(t, p)
plt.ylim(-0.0001, p.max()*1.1) #y축 범위 지정
plt.xticks([0, 180, 360])

plt.title("확률밀도함수")
plt.xlabel("$x$ (도)")
plt.ylabel("$p(x)$")

plt.show()

rv = stats.norm(0,1) # 평균0, 표준편차1
x = np.linspace(-5,5,100) # 동일 간격으로 -5부터 5까지 100개 생성
y1 = rv.pdf(x) # pdf : 확률밀도함수
plt.plot(x,y1)
plt.show()

💡 확률변수와 상관관계

#한글 폰트 설정
from matplotlib import font_manager, rc
import matplotlib.pyplot as plt

font_location = "c:/Windows/fonts/malgun.ttf"
font_name = font_manager.FontProperties(fname=font_location).get_name()
rc('font', family=font_name)

• 확률적 데이터 : 예측할 수 없는 값이 나오는 데이터
• 분포 : 어떠한 값이 자주 나오고 어떠한 값이 드물게 나오는가를 나타내는 정보

정규분포로부터 21개의 무작위 샘플 추출

np.random.seed(0)
x = np.random.normal(size=21)  #정규분포로부터 21개의 무작위 샘플 추출
x

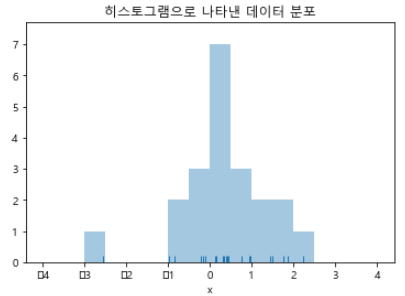
히스토그램으로 데이터 분포 표현

import seaborn as sns

bins = np.linspace(-4, 4, 17)
#rug: 데이터 위치를 x축 위에 작은 선분으로 표현
#kde: 막대그래프를 연속적으로 부드럽게 표현
#bins: 만약 bins가 2면 2개의 막대로 분포 표현
sns.distplot(x, rug=True, kde=False, bins=bins)  #히스토그램 생성
plt.title("히스토그램으로 나타낸 데이터 분포")
plt.xlabel("x")
plt.show()

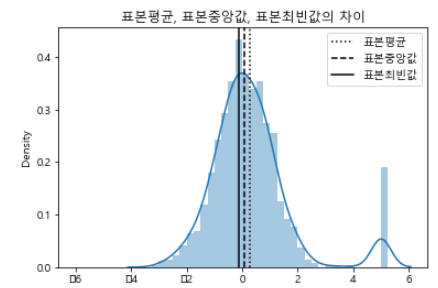
표본평균/표본중앙값/최빈구간(표본최빈값) + 대칭분포

• 표본평균 : 표본집단의 평균 값
• 표본중앙값 : 가장 중앙에 위치하는 값
• 표본최빈값 : 가장 빈번하게 관찰/측정되는 값
• mean() : 표본평균 계산
• median() : 표본중앙값 계산
• argmax() : 이산데이터의 최댓값 계산
• histogram() : 데이터를 구간으로 나누어 각 구간에 들어가는 데이터 개수 계산.

print("표본평균 = {}, 표본중앙값 = {}".format(np.mean(x), np.median(x)))

ns, _ = np.histogram(x, bins=bins)  #(각 구간에 있는 data 수, 구분구간)을 반환
m_bin = np.argmax(ns)  #data 수의 최댓값 계산
print("최빈구간 = {}~{}".format(bins[m_bin], bins[m_bin + 1]))  #최빈구간

대칭분포 (표본평균, 표본중앙값, 표본최빈값 계산)

• (분포가 표본평균을 기준으로 대칭인)대칭분포 → 표본중앙값 = 표본평균
• (대칭분포이면서 하나의 최고값만을 가지는)단봉분포 → 표본최빈값 = 표본평균
• 대칭분포를 비대칭으로 만드는 데이터가 더해지면 표본평균이 가장 크게 영향을 받고 표본최빈값이 가장 적게 영향을 받음.

from sklearn.datasets import load_iris
import pandas as pd

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
sy = pd.Series(iris.target, dtype="category")
sy = sy.cat.rename_categories(iris.target_names)
df['species'] = sy

np.random.seed(1)
x = np.random.normal(size=1000)  #정규분포로부터 1000개의 무작위 샘플 추출
#hstack:두 배열을 가로로 이어붙임. / ones:1로 가득찬 배열 생성
x = np.hstack([x, 5 * np.ones(50)])  

bins = np.linspace(-6, 6, 12 * 4 + 1)
ns, _ = np.histogram(x, bins=bins)

sample_mean = np.mean(x)  #x축을 따라 배열의 평균 계산
sample_median = np.median(x)  #중앙값 계산
mode_index = np.argmax(ns)  #최댓값 계산
sample_mode = 0.5 * (bins[mode_index] + bins[mode_index + 1]) #표본최빈값 계산

sns.distplot(x, bins=bins)
plt.axvline(sample_mean, c='k', ls=":", label="표본평균")
plt.axvline(sample_median, c='k', ls="--", label="표본중앙값")
plt.axvline(sample_mode, c='k', ls="-", label="표본최빈값")
plt.title("표본평균, 표본중앙값, 표본최빈값의 차이")
plt.xlabel("x")
plt.legend()
plt.show()

표본분산과 표준편차

sp.random.seed(0)
# 평균=0, 표준편차=2인 정규분포 데이터 생성 (표본값 100개 생성)
x = sp.stats.norm(0, 2).rvs(1000) 
np.var(x), np.std(x) # 편향 표본분산, 표본표준편차

np.var(x, ddof=1), np.std(x, ddof=1)  # 비편향 표본분산, 표본표준편차

왜도와 첨도

• 왜도 : 분포의 비대칭도를 나타내는 통계량 (대칭분포의 경우 왜도가 0)
• 첨도 : 분포의 꼬리부분의 길이와 중앙부분의 뾰족함에 대한 정보를 제공하는 통계량

# 왜도와 표본첨도
sp.stats.skew(x), sp.stats.kurtosis(x)  #각각 값을 리턴

표본모멘트

• 분산, 비대칭도, 첨도를 구하기 위해 k제곱을 이용하여 구한 모멘트

sp.stats.moment(x, 1), sp.stats.moment(x, 2), sp.stats.moment(x, 3), sp.stats.moment(x, 4)

기댓값

• 예제 01

x = np.linspace(-100, 500, 1000)
p = np.zeros_like(x)
p[(0 < x) & (x <= 360)] = 1 / 360
xp = x * p

plt.subplot(121)
plt.plot(x, p)
plt.xticks([0, 180, 360])
plt.title("$p(x)$")
plt.xlabel("$x$ (도)")

plt.subplot(122)
plt.plot(x, xp)
plt.xticks([0, 180, 360])
plt.title("$xp(x)$")
plt.xlabel("$x$ (도)")

plt.show()

• 예제 02

x = np.linspace(-100, 500, 1000)
p = np.zeros_like(x)
p[(0 < x) & (x <= 180)] = 2 / (3 * 360)
p[(180 < x) & (x <= 360)] = 1 / (3 * 360)
xp = x * p

plt.subplot(121)
plt.plot(x, p)
plt.xticks([0, 180, 360])
plt.title("$p(x)$")
plt.xlabel("$x$ (도)")

plt.subplot(122)
plt.plot(x, xp)
plt.xticks([0, 180, 360])
plt.title("$xp(x)$")
plt.xlabel("$x$ (도)")\

plt.show()

상관계수와 공분산

• 공분산 : 2개의 확률변수의 상관정도를 나타내는 값

np.cov(X, Y)
#np.cov(X, Y)[0, 1]

• 상관계수 : 공분산을 표준화시킨 값

np.corrcoef(X, Y)
#np.corrcoef(X, Y)[0, 1]