[#알고리즘/위상 정렬/[백준]1516번: 게임 개발(python)]

Question

https://www.acmicpc.net/problem/1516

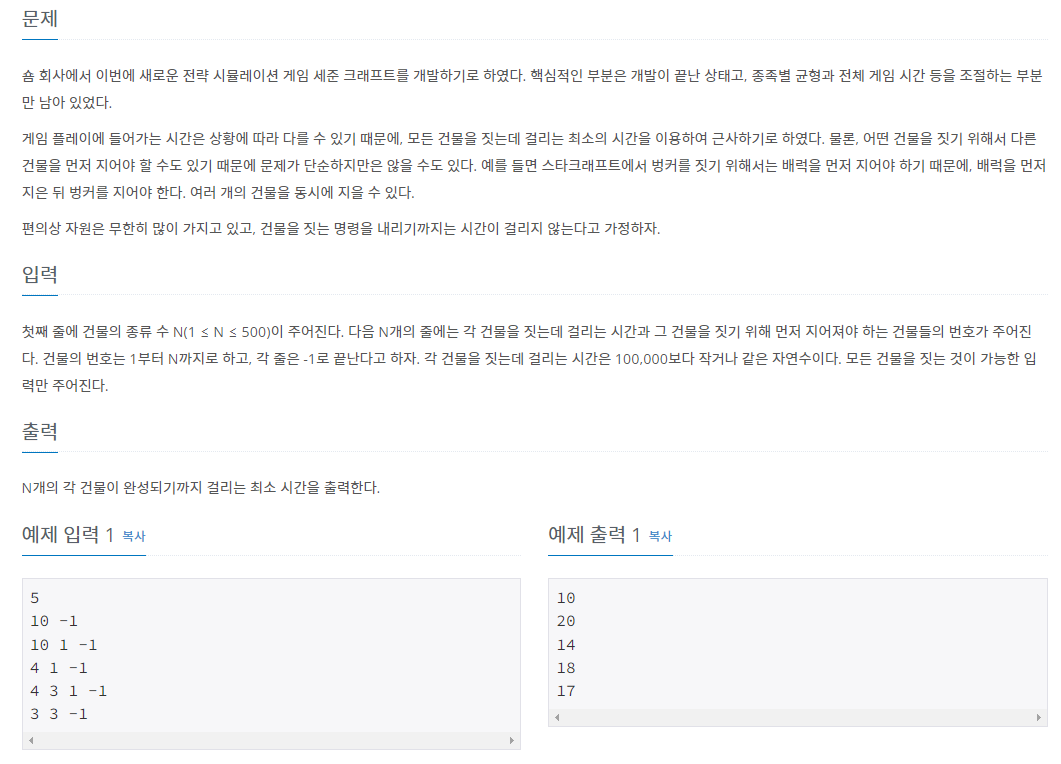
(선수 건물 : N번 건물을 짓기 위해 먼저 지어야 하는 건물)

입력 예시를 보면, 1번 건물을 짓기 위해선 10시간이 걸리며, 1번 건물의 선수 건물은 없다.
2번 건물을 짓기 위해선 10시간이 걸리며 1번 건물을 먼저 지어야 한다.

Solution

위상정렬 알고리즘의 응용 문제이다. 예를 들어, 진입차수가 0인 노드(건물) a를 큐에서 꺼내 a로부터 인접한 노드 b를 확인할 때, 노드 b의 선수 노드 중(a 포함) 가장 오랜 시간이 걸리는 노드에 노드 b의 시간을 더한 결과가 답이 된다. 아래 예시를 보고 이해하자.

ex) 3번 건물(노드 b)를 짓기 위해선 1번 건물(노드 a)과 2번 건물(노드 c)을 지어야 한다. 1번 건물과 2번 건물에 대해선 선수 건물이 없고, 건물을 짓는 데 각각 4초, 2초가 걸린다. 3번 건물을 짓는 데는 6초가 걸린다. 이때 3번 건물을 짓기 위한 최소 시간은 8(2 + 6)초가 아닌 10(4 + 6)초이다. 2 + 6초인 경우, 2번 건물은 지을 수 있지만 1번 건물을 짓는데는 시간이 부족하다. (건물은 동시에 지을 수 있다.) 따라서 4 + 6초여야 1번, 2번 건물 모두 지을 수 있으며 그에 따라 3번 건물을 지을 수 있다.

또한 처음에 각 건물을 짓는데 걸리는 시간을 time 리스트에 담았는데, 위상정렬 함수에서 deepcopy() 함수를 사용하여 time 리스트 값을 복사해 result 리스트 값으로 설정하는 작업이 수행된다. 리스트의 경우, 단순히 대입 연산을 하면 값이 변경될 때 문제가 발생할 수 있으므로, 리스트의 값을 복제할 때는 deepcopy() 함수를 사용하자.

Code

from collections import deque
import copy
import sys

input =  sys.stdin.readline

# 건물(노드)의 수
n = int(input())
# 모든 건물에 대한 진입차수는 0으로 초기화
indegree = [0] * (n + 1)
# 각 건물(노드)에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
graph = [[] for _ in range(n + 1)]
# 각 건물을 짓는데 걸리는 시간을 0으로 초기화
time = [0] * (n + 1)

# 모든 간선 정보 입력받기
for i in range(1, n + 1) :
    data = list(map(int, input().split()))
    time[i] = data[0]
    for x in data[1 : -1] :
        indegree[i] += 1
        graph[x].append(i)
        
# 위상 정렬 함수
def topology_sort() :
    result = copy.deepcopy(time)  # 위상정렬 수행 결과를 담을 list
    q = deque()
    
    # 처음 시작 시 진입차수가 0인 노드를 큐에 삽입
    for i in range(1, n + 1) :
        if indegree[i] == 0 :
            q.append(i)
            
    while q :
        now = q.popleft()
        for x in graph[now] :
            result[x] = max(result[x], result[now] + time[x])
            indegree[x] -= 1
            if indegree[x] == 0 :
                q.append(x)
                
    # 위상 정렬 수행 결과 출력
    for i in range(1, n + 1) :
        print(result[i])
        
topology_sort()