Chap10. Dynamic Programming(DP)

Optimazation Programming을 해결할 수 있는 기법 중 하나
Divide and Conquer 전략과 유사함
- 문제를 여러 개의 subproblem으로 쪼개어 해결, 차이점은 한번 계산한 solution은 table에 저장해두고 다시 계산하지 않는다는 것, 따라서 메모리 사용량이 적고 속도가 빠름

1. top-down 방법(memorization 방법) : recursion
2. bottom-up 방법 : loop

Dynamic Programming Version of a Recursive Algorithm

top-down 방식

subproblems의 solution을 저장함으로써 space는 더 사용하되 속도를 개선

기존에 계산했는지 dictionary(soln/table로도 불림)를 확인한 후,

• solution이 저장되지 않았다면 recursive call을 이용하여 계속 계산
• solution이 저장되어 있다면 저장된 내용을 dictionary에서 찾아서 바로 활용

Example :: fib

/* top-down 방식 */
fibDPwrap(n)
	Dict soln = create(n);	// size=n인 table
	return fibDP(soln,n);
fibDP(soln,k)			// 실제 피보나치 계산
	int fib, f1, f2;
	if (k < 2) fib = k;	// base case
	else if (member(soln,k-1) == false) f1 = fibDP(soln,k-1);
		else f1 = retrieve(soln,k-1);
		if (member(soln,k-2) == false) f2 = fibDP(soln,k-2);
		else f2 = retrieve(soln,k-2);
		fib = f1 + f2;
	store(soln,k,fib);
	return fib;

$F_{10}$ = $F_9$ + $F_8$
$F_9$ = $F_8$ + $F_7$
...
중복되는 값이 매우 많음, 이 문제를 해결

/* bottom-up 방식 */
f_0 = 0, f_1 = 1;
for i=2 to n
	f_i = f_(i-1) + F_(i-2);

Matrix-Chain Multiplication

DP를 이용해서 해결할 수 있는 optimazation problem의 예시
[문제]
n개의 matrices <A1, A2, ..., An> 나열이 주어지면, 곱셈 횟수가 가장 적은 경우 찾기
[입력]
n개의 matrices chain <A1, A2, ..., An>, 혹은 차원 정보 <P0, P1, ..., Pn>
이때 matrix Ai의 차원이 $p_{i-1}$ * $p_i$로 주어졌을 때
[출력]
scalar multiplications을 최소화하는 행렬 곱셈의 순서
즉, 괄호를 어떻게 묶어야 하는지 fully parenthesize 계산

Computation Time

두 개의 matrices를 곱할 때의 연산, 각각은 pq, qr의 차원을 가짐

필요한 multiplication 연산의 수는 pqr --> pr개의 elements가 각각 q만큼의 계산을 거침

Development
1. Optimal solution을 계산하기 위한 구조의 특징을 파악
2. Optimal solution의 값을 recursive하게 정의 - 점화식 정의
3. 점화식을 이용하여 optimal solution의 value값 계산, bottom-up
4. optional step::optimal solution 자체를 생성

Step 1 :: Optimal solution의 구조 파악
$A_i$$A_{i+1}$...$A_j$를 $A_i$...$A_k$와 $A_{k+1}$...$A_j$로 쪼갬

• cost = subX계산비용 + subY계산비용 + 전체곱셈비용

Step 2 :: 구조를 이용하여 점화식 생성
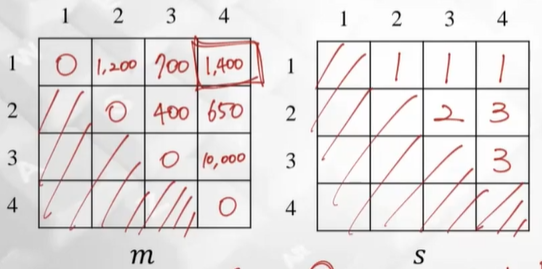
table m[i,j]: optimization value를 저장할 table. 필요한 scalar multiplication의 최소 횟수

• 0 if i=j, matrix-chain의 size=1
• min {m[i,k] + m[k+1,j] + $p_{i-1}$$p_k$$p_j$} if i < j, size>2

* m[i,k]의 dimention은 $P_{i-1}$$P_k$, m[k+1,j]의 dimention은 $P_k$$P_j$
table s[i,j]: 최소 횟수를 저장할 때의 k값을 저장하는 table

Step 3 :: 점화식을 이용한 계산
m, s table을 이용하여 bottom-up 방식으로 계산
input : p=<p0,p1,...,pn>, 차원 정보만 주어짐
m[1..n, 1..n]과 s[1..n, 1..n]인 size가 n*n인 table 이용

/* MATRIX-CHAIN-ORDER(𝑝) */
1 	𝑛 ← 𝑙𝑒𝑛𝑔𝑡ℎ 𝑝 − 1
2 	for 𝑖 ← 1 to 𝑛
3 		do 𝑚[𝑖, 𝑖] ← 0
4 	for 𝑙 ← 2 to 𝑛 	// 𝑙 is the chain length.
5 		do for 𝑖 ← 1 to 𝑛 − 𝑙 + 1
6 			do 𝑗 ← 𝑖 + 𝑙 − 1
7 				𝑚[𝑖,𝑗] ← ∞
8 				for 𝑘 ← 𝑖 to 𝑗 − 1
9 					do 𝑞 ← 𝑚 𝑖, 𝑘 + 𝑚 𝑘 + 1,𝑗 + 𝑝𝑖−1𝑝𝑘𝑝𝑗
10 						if 𝑞 < 𝑚[𝑖,𝑗]
11 							then 𝑚[𝑖,𝑗] ← 𝑞
12 								𝑠[𝑖,𝑗] ← 𝑘
13  return 𝑚 and s

m[i,j] = min{m[i,k]+m[k+1,j]+$p_{i-1}$$p_k$$p_j$}