미확인 도착지

알고리즘 구분 : 그래프 이론, 다익스트라

문제

(취익)B100 요원, 요란한 옷차림을 한 서커스 예술가 한 쌍이 한 도시의 거리들을 이동하고 있다. 너의 임무는 그들이 어디로 가고 있는지 알아내는 것이다. 우리가 알아낸 것은 그들이 s지점에서 출발했다는 것, 그리고 목적지 후보들 중 하나가 그들의 목적지라는 것이다. 그들이 급한 상황이기 때문에 목적지까지 우회하지 않고 최단거리로 갈 것이라 확신한다. 이상이다. (취익)

어휴! (요란한 옷차림을 했을지도 모를) 듀오가 어디에도 보이지 않는다. 다행히도 당신은 후각이 개만큼 뛰어나다. 이 후각으로 그들이 g와 h 교차로 사이에 있는 도로를 지나갔다는 것을 알아냈다.

이 듀오는 대체 어디로 가고 있는 것일까?

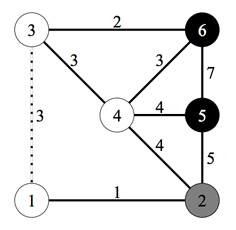
예제 입력의 두 번째 케이스를 시각화한 것이다. 이 듀오는 회색 원에서 두 검은 원 중 하나로 가고 있고 점선으로 표시된 도로에서 냄새를 맡았다. 따라서 그들은 6으로 향하고 있다.

입력
첫 번째 줄에는 테스트 케이스의 T(1 ≤ T ≤ 100)가 주어진다. 각 테스트 케이스마다

첫 번째 줄에 3개의 정수 n, m, t (2 ≤ n ≤ 2 000, 1 ≤ m ≤ 50 000 and 1 ≤ t ≤ 100)가 주어진다. 각각 교차로, 도로, 목적지 후보의 개수이다.
두 번째 줄에 3개의 정수 s, g, h (1 ≤ s, g, h ≤ n)가 주어진다. s는 예술가들의 출발지이고, g, h는 문제 설명에 나와 있다. (g ≠ h)
그 다음 m개의 각 줄마다 3개의 정수 a, b, d (1 ≤ a < b ≤ n and 1 ≤ d ≤ 1 000)가 주어진다. a와 b 사이에 길이 d의 양방향 도로가 있다는 뜻이다.
그 다음 t개의 각 줄마다 정수 x가 주어지는데, t개의 목적지 후보들을 의미한다. 이 t개의 지점들은 서로 다른 위치이며 모두 s와 같지 않다.
교차로 사이에는 도로가 많아봐야 1개이다. m개의 줄 중에서 g와 h 사이의 도로를 나타낸 것이 존재한다. 또한 이 도로는 목적지 후보들 중 적어도 1개로 향하는 최단 경로의 일부이다.

출력
테스트 케이스마다

입력에서 주어진 목적지 후보들 중 불가능한 경우들을 제외한 목적지들을 공백으로 분리시킨 오름차순의 정수들로 출력한다.
예제 입력 1
2
5 4 2
1 2 3
1 2 6
2 3 2
3 4 4
3 5 3
5
4
6 9 2
2 3 1
1 2 1
1 3 3
2 4 4
2 5 5
3 4 3
3 6 2
4 5 4
4 6 3
5 6 7
5
6
예제 출력 1
4 5
6

문제 풀이

문제를 읽자마자 문제 내의 최단 거리라는 표현이 명시되어 있으므로 다익스트라 알고리즘을 이용한 구현이라고 생각하였다. 여기서 문제 풀이의 핵심은 크게 두 가지가 있다. 첫 번째는 g노드와 h노드 사이의 연결된 간선을 활용해도 최단거리이지만 정렬 순서에 의해 g노드와 h노드 사이 간선을 사용하지 않는 경우가 발생할 수 있는데, 이에 대한 처리를 어떻게 할 것인가와 g노드와 h노드 사이의 연결된 간선을 이용하는지 여부에 따른 가능한 목적지 리스트를 찾는 부분이 핵심이였는데 이 부분에서 많은 시간을 투자하였기에 정리해보려고 한다.

첫 번째 g노드와 h노드 사이의 연결된 간선을 활용해도 최단거리이지만, 다른 간선을 활용해도 최단거리가 될 수 있는 경우에 대한 해답은 명확했다. 다른 분들의 풀이를 보니, 다익스트라를 총 3번 하는 과정을 거쳐 g-h간선을 무조건적으로 활용했을 때의 거리가 일반 다익스트라를 활용해서 나온 최단거리와 동일할 경우, g-h간선을 활용한 경우로 간주하는 방식을 풀었는데, 나는 질문 게시판의 도움을 받아 일종의 Ad-hoc으로 거리를 저장하는 방식을 다르게 하였다.

if((a == g && b == h) || (a == h && b == g)) {
    d = pow(d, 2) - 1;
}
else {
    d = pow(d, 2);
}

위 소스 코드를 확인해보면, g-h 간선일 경우는 2를 곱한 후 - 1을 하여 작은 크기를 가진 간선으로 바꾸었고, 나머지 간선은 크기에 2를 곱한 값이 해당 간선의 크기가 되도록 변환하였다. 이렇게 되면 동일한 크기를 가진 간선이라도 1이 작은 g-h간선을 우선순위로 활용할 수 있게 된다.

두 번째를 해결하기 위해서는 다양한 방법을 시도해보았다.

첫 번째로, 단 해당 간선을 이용해서 최단 거리를 완성했는지에 대한 여부를 확인하는 방법으로 bool 배열을 활용했다. 방문 처리할 때 사용하는 배열처럼 지금 확인하고 있는 간선이 g노드와 h노드 사이 간선이거나, 해당 간선을 사용해서 넘어온 간선을 활용하고 있으면 true를, 그렇지 않거나, 새로이 최단 거리를 갱신했을 때 g노드와 h노드 사이의 간선을 활용하고 있지 않다면 false로 갱신하는 방법을 취했었다.

if(!visited[graph[now][i].first]) {
                    if(visited[now]) {
                        visited[graph[now][i].first] = true;
                    }

                    if((now == g && graph[now][i].first == h) || (now == h && graph[now][i].first == g)) {
                        visited[graph[now][i].first] = true;
                    }
                }
                else {
                    if(!visited[now]) {
                        visited[graph[now][i].first] = false;
                    }
                }

위의 방식으로 조건문을 짰으나, TC는 잘 작동하지만 WA(33%)를 받았다.

위의 거리를 갱신하는 방식을 활용하도록 바꾸어서 시도해보았다.
어떤 수에 2를 곱하면 늘 짝수이고, g-h간선을 활용하면 홀수가 더해지게 된다. 수학적으로 짝수 + 짝수 = 짝수이지만, 짝수 + 홀수 = 홀수가 나온다. 즉, g-h간선을 활용하면 홀수가 나오게 되므로, 최단거리가 홀수일 경우를 g-h간선을 활용한 것으로 간주하였다.
해당 방식으로 제출하였더니 AC를 받았다.

위의 과정을 진행할 때, 처음엔 INF를 987654321로 놓았다 WA를 받았다. 이 부분에 대하여 좀 찾아보다보니, 최단 거리가 갱신되지 못하고 INF 상태로 놓여있어도 이를 홀수로 간주하는 경우가 발생하기 때문이였다. 그래서 위와 같이 INF도 짝수로 선언하였다.

소스 코드

#include <bits/stdc++.h>

using namespace std;

#define endl "\n"
#define INF 200000000

int T, n, m, t, s, g, h;
vector<pair<int, int>> graph[2001];
int dist[2001];
//bool visited[2001];
vector<int> dest;
void dijkstra(int start);

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin >> T;
    while(T--) {
        fill(&dist[0], &dist[0] + sizeof(dist) / sizeof(int), INF);
        memset(graph, 0, sizeof(graph));
        //memset(visited, 0, sizeof(visited));
        vector<int>().swap(dest);

        cin >> n >> m >> t;
        cin >> s >> g >> h;

        for(int i = 0; i < m; i++) {
            int a, b, d;
            cin >> a >> b >> d;
            if((a == g && b == h) || (a == h && b == g)) {
                d = d * 2 - 1;
            }
            else {
                d = d * 2;
            }

            graph[a].push_back({b, d});
            graph[b].push_back({a, d});
        }

        for(int i = 0; i < t; i++) {
            int x;
            cin >> x;
            dest.push_back(x);
        }

        dijkstra(s);
    }

    return 0;
}

void dijkstra(int start) {
    vector<int> result;
    priority_queue<pair<int, int>, vector<pair<int, int>>, less<pair<int, int>>> pq;

    dist[start] = 0;
    pq.push({0, start});

    while(!pq.empty()) {
        int now = pq.top().second;
        int cost = pq.top().first;

        pq.pop();

        if(cost > dist[now]) {
            continue;
        }

        for(int i = 0; i < graph[now].size(); i++) {
            if(cost + graph[now][i].second < dist[graph[now][i].first]) {
                /*
                cout << now << " " << graph[now][i].first << endl;
                cout << visited[now] << " " << visited[graph[now][i].first] << endl;
                */

                /*     
                // 최단 경로 시 해당 경로 지나는지 여부 갱신
                if(!visited[graph[now][i].first]) {
                    if(visited[now]) {
                        visited[graph[now][i].first] = true;
                    }

                    if((now == g && graph[now][i].first == h) || (now == h && graph[now][i].first == g)) {
                        visited[graph[now][i].first] = true;
                    }
                }
                else {
                    if(!visited[now]) {
                        visited[graph[now][i].first] = false;
                    }
                }
                */

                dist[graph[now][i].first] = cost + graph[now][i].second;
                pq.push({cost + graph[now][i].second, graph[now][i].first});
            }
        }
    }

    /*
    for(int i = 1 ; i < n + 1; i++) {
        cout << visited[i] << " ";
    }
    cout << endl;
    
    for(int i = 1 ; i < n + 1; i++) {
        cout << dist[i] << " ";
    }
    cout << endl;
    */    

    for(int i = 0; i < dest.size(); i++) {
        if(dist[dest[i]] % 2 != 0) {
            result.push_back(dest[i]);
        }
    }

    sort(result.begin(), result.end(), less<int>());

    for(int i = 0; i < result.size(); i++) {
        cout << result[i] << " ";
    }
    cout << endl;
}

• 문제 출처 : https://www.acmicpc.net/problem/9370
• 해당 풀이는 백준에서 "맞았습니다!!" 판정을 받았습니다.