재귀함수와 꼬리 재귀

도입

최근 넓이 우선 탐색(BFS)과 깊이 우선 탐색(DFS) 알고리즘 문제를 풀었다. BFS는 큐(Queue)를 사용한 반복문으로 구현을 하고, DFS는 재귀함수로 구현하여 문제를 풀었다.
(물론 DFS는 스택(Stack)을 이용하여 반복문으로도 구현할 수 있다)

일반적으로 재귀함수보다 반복문의 실행 속도가 더 빠른 것으로 알고 있는데, 어째서 그러한 차이가 나는지 궁금해졌다.
그래서 이번 포스팅에서 재귀과 반복의 차이, 그리고 꼬리 재귀 최적화에 대하여 다뤄보았다.

재귀(Recursive) vs 반복(Iteration)

반복과 재귀의 가장 큰 차이는, 재귀는 스스로를 호출한다는 점에 있다.

• 반복문으로 구현한 팩토리얼

int factorial(int num){
  int result = 1;
  for(int i = 1 ; i <= num ; i++){
      result = result * i;
  }
  return result;
}

• 재귀로 구현한 팩토리얼

int factorial(int n){
	if(n == 1) return 1;
    return n * factorial(n - 1);
}

아래에서는 두 방식을 여러 관점에서 비교를 하였다.

시간 복잡도 계산의 난이도

재귀가 반복보다 시간 복잡도 계산이 어렵다.

• 재귀
  재귀의 시간 복잡도는 이전 호출의 입장에서 n번째 재귀 호출의 값을 알아내면 알 수 있다.
  그러므로 종결 조건(Terminating case, Base case) 입장에서 목적 조건(Destination case)을 찾고, 종결 조건 입장에서 해결하는 것이 재귀식의 시간 복잡도를 계산하는 것의 아이디어가 된다.
  재귀는 시간 복잡도를 계산하는 것이 어렵다.

• 반복
  반복의 시간 복잡도는 비교적 간단히 루프 내의 반복되는 사이클의 수를 알아내면 알 수 있다.

종결 조건(Terminating case, Base case)
어떠한 후속 재귀 호출 없이 값을 반환하는 경우. 재귀를 끊으며, 재귀 함수는 이것을 하나 이상 가진다.
팩토리얼 재귀함수를 예로 들면, if(n == 0)이 종결 조건이 된다.

언제 사용하는가?

두 방식은 시간 복잡도와 코드의 양에서 상호교환적(Trade-off)인 측면을 보인다.
시간 복잡도의 측면에서 보면, 재귀 호출의 수는 클 것이고 반복을 쓰는 것이 좋을 수 있다. 하지만 코드의 길이를 중점으로 한다면, 재귀가 나을 수 있다.

• 재귀
  재귀는 같은 함수를 호출하고 호출한다. 때문에 코드의 길이는 짧다. 그러나 분석을 해보면, 호출이 상당히 많아지면 시간 복잡도가 지수 단위(Exponential)로 증가할 수 있다.
  그러므로, 재귀의 사용은 짧은 코드라는 점에서 이점이지만, 반복보다 높은 시간 복잡도를 가진다.

• 반복
  코드 블록의 반복이다. 이것은 코드가 길어지게 되지만, 일반적으로 재귀보다 낮은 시간 복잡도를 가진다.

오버헤드

재귀는 반복과 비교하여 큰 오버헤드를 가진다.

• 재귀
  재귀는 반복되는 함수 호출에서 오버헤드를 가진다.
  이는 동일한 함수를 반복 호출하는 것이 코드의 시간 복잡도가 증가하는 점을 말한다.

• 반복
  반복은 그러한 오버헤드를 가지지 않는다.

재귀 함수가 가지는 Stack 오버헤드
함수 호출은 Stack 기반으로 작동 한다. 함수가 호출될 때마다 함수는 스택에 쌓이게 된다. 매개변수, 리턴값, 리턴되었을 때 돌아갈 위치 등의 정보가 스택에 저장된다.
재귀함수는 하나의 함수가 실행이 끝나지 않은 채 함수를 연속적으로 호출하여 Stack에 계속 쌓이게 된다.
더 이상 메모리가 감당할 수 없게 되면 Stack overflow가 발생하게 된다.

무한 반복

무한 반복이 발생하는 경우 재귀는 CPU 크래시를 초래할 수 있지만, 반복은 메모리가 부족할 때가 되면 멈춘다.

• 재귀
  종결 조건을 명시할 때 실수를 하면, 무한 재귀 호출이 생길 수 있다.
  예를들어 조건이 false가 되지 않아 계속 함수를 호출하게 되면 CPU 크래시가 발생할 수 있다.

• 반복
  반복자 실수(반복자 배정이나 증가) 혹은 종료 조건(terminating condition)을 실수하면 무한 루프가 발생한다.
  시스템 에러가 발생할 수도, 발생하지 않을 수도 있지만 어쨋든 프로그램이 확실하게 중지될 것이다.

재귀를 왜쓰는가?

위에서 반복과 재귀를 비교해 보았는데, 재귀가 반복에 비하여 가진 단점이 너무나도 많다.
그럼에도 불구하고 재귀를 쓰는 이유가 무엇일까?

• 알고리즘 자체가 재귀적으로 표현하기 자연스러울 때, 가독성이 좋다.
• 변수 사용을 줄여준다.

꼬리 재귀

재귀로 구현을 하고 싶은데, 재귀가 가지는 오버헤드 때문에 마음이 편치 않을 수 있다.
하지만 꼬리 재귀 최적화를 이용하면 오버헤드를 피하면서 재귀문을 작성할 수 있다!

꼬리 재귀 최적화를 적용하려면 아래 2가지 조건이 필요하다.

꼬리 재귀 최적화를 위한 조건 2가지

• 재귀 함수를 꼬리 재귀 방식으로 구현할 것
• 컴파일러가 꼬리 재귀 최적화를 지원할 것

컴파일러가 꼬리 재귀 최적화를 지원하지 않는다면, 꼬리 재귀 방식으로 구현을 해도 일반 재귀처럼 동작할 것이다.

꼬리 재귀 방식으로 구현하기

일반 재귀 팩토리얼

int factorial(int n){
	if(n == 1) return 1;
    return n * factorial(n - 1);
}

위에서 일반 재귀 방식으로 구현한 팩토리얼 함수를 가져왔다.
이것을 꼬리 재귀 방식으로 고쳐보자.

꼬리 재귀 팩토리얼

int factorialTail(int n, int acc){
	if(n == 1) return acc;
    return factorialTail(n - 1, acc * n);
}
int factorial(int n){
    return factorialTail(n, 1);
}

팩토리얼 함수가 두개로 분리되었는데, 요점은 재귀 호출 이후 추가적인 연산을 요구하지 않도록 구현하는 것이다.

일반 재귀 팩토리얼은 추가 연산이 존재
일반 재귀로 구현된 factorial 함수는 재귀 호출을 하고 나서, num 을 곱하는 연산이 존재한다.
따라서 일반 재귀로 구현된 함수는 아래 함수와 같이 동작한다.

int factorial(int num){
	if(num == 0) return 1;
    int callResult = factorial(num - 1);
    return num * callResult;			// 재귀 호출 이후 추가적인 연산이 필요하다.
}

반면 꼬리 재귀로 구현된 함수는 factorialTail이 호출 이후 연산이 없다.

컴파일러의 해석

꼬리 최적화를 하면 컴파일러는 코드를 아래와 같이 해석한다.

int FactorialTail(int n){
	int acc = 1;
    
    do{
    	if(n == 1) return;
        acc = acc * n;
        n = n - 1;
    } while(true);
}

이렇게 내부적으로 재귀 함수를 반복문으로 변경되어 실행이 되고, 실제 스택도 여러 번 호출하는 것이 아닌 한번만 호출한다.

Java와 꼬리 재귀 최적화

C++, C#, Kotlin, Swift은 꼬리 재귀 최적화를 지원하며, JavaScript는 ES6 스펙에서 지원한다고 한다.
Scala는 JVM 위에서 동작하는데, 꼬리 재귀 최적화를 지원한다고 한다.
하지만 Java는 꼬리 재귀 최적화를 직접적으로 지원하지 않는다.

지원하지 않는 이유
jdk 클래스에는 보안에 민감한 메소드가 있다고 한다. 이 메소드들은 메소드 호출을 누가 했는지 알아내기 위해 jdk 라이브러리 코드와 호출 코드간의 스택 프레임 갯수에 의존한다. 스택 프레임 수의 변경을 유발하게 되면 이 의존관계를 망가뜨려 에러가 발생할 수 있다.
출처

실제로 최적화가 이루어지지 않는지 디컴파일러로 확인해보았다.

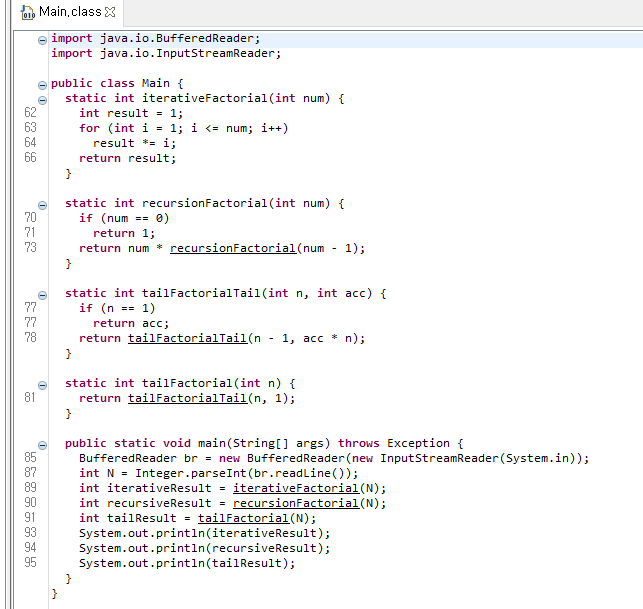
컴파일된 .class 파일을 디컴파일해서 보니 꼬리 재귀 최적화가 되어있지 않았다.

Java에서 꼬리 재귀 사용하기?
Java는 컴파일러 레벨에서는 직접적으로 꼬리 재귀 최적화를 지원하지는 않지만, Java 8의 람다식과 함수형 인터페이스(functional interface)로, 꼬리 재귀와 같은 컨셉을 적용해볼 수 있다고 한다.
아래에 이에 대해 잘 설명된 글이 있어 링크를 남겨놓았으니 참고해보기 바란다.
링크

참고자료

https://www.geeksforgeeks.org/difference-between-recursion-and-iteration/
https://introcs.cs.princeton.edu/java/23recursion/
https://en.wikipedia.org/wiki/Recursion_(computer_science)
https://blockdmask.tistory.com/321
https://joosjuliet.github.io/tail_recursion/
https://medium.com/sjk5766/%EC%9E%AC%EA%B7%80%ED%95%A8%EC%88%98%EB%A5%BC-%EC%93%B0%EB%8A%94-%EC%9D%B4%EC%9C%A0-ed7c37d01ee0
https://bozeury.tistory.com/entry/%EA%BC%AC%EB%A6%AC-%EC%9E%AC%EA%B7%80-%EC%B5%9C%EC%A0%81%ED%99%94Tail-Recursion
https://blog.knoldus.com/tail-recursion-in-java-8/