Classifier Free Guidance

이의찬·2024년 6월 10일

Classifier Guidance

score function

score function: ∇log⁡p(xt)=−11−αˉtϵθ(xt)\nabla \log p(\mathbf{x}_t) = - \frac{1}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_{\theta}(\mathbf{x}_t)

-likelihood의 gradient 방향으로 이동하면 우도가 높아짐



∇log⁡p(xt∣y)=∇log⁡(p(xt)p(y∣xt)p(y))\nabla \log p(x_t \mid y) = \nabla \log \left( \frac{p(x_t)p(y \mid x_t)}{p(y)} \right)
=∇log⁡p(xt)+∇log⁡p(y∣xt)−∇log⁡p(y)= \nabla \log p(x_t) + \nabla \log p(y \mid x_t) - \nabla \log p(y)
=∇log⁡p(xt)⏟unconditional score+∇log⁡p(y∣xt)⏟adversarial gradient= \underbrace{\nabla \log p(x_t)}_{\text{unconditional score}} + \underbrace{\nabla \log p(y \mid x_t)}_{\text{adversarial gradient}}



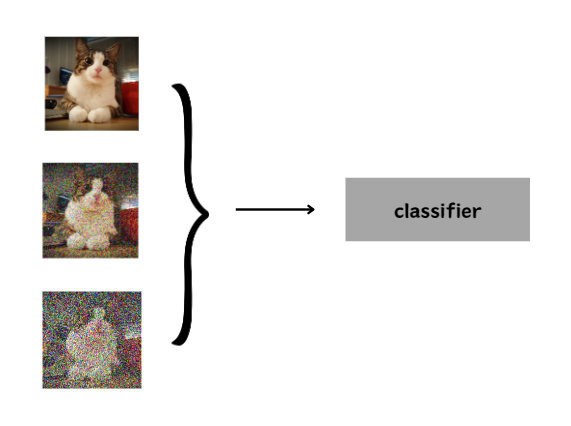
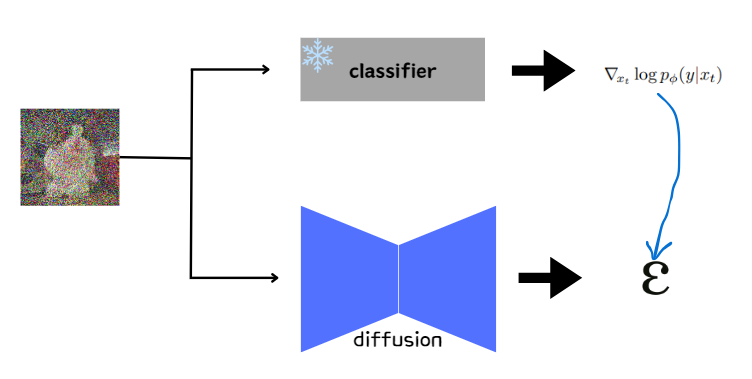
∇log⁡p(xt∣y)=∇log⁡p(xt)+γ∇log⁡p(y∣xt)\nabla \log p(x_t \mid y) = \nabla \log p(x_t) + \gamma \nabla \log p(y|x_t)



classifier free guidance

∇log⁡p(xt)⏟unconditional score+∇log⁡p(y∣xt)⏟adversarial gradient\underbrace{\nabla \log p(x_t)}_{\text{unconditional score}} + \underbrace{\nabla \log p(y \mid x_t)}_{\text{adversarial gradient}}



∇log⁡p(y∣xt)=∇log⁡p(xt∣y)−∇log⁡p(xt)\nabla \log p(y \mid \mathbf{x}_t) = \nabla \log p(\mathbf{x}_t \mid y) - \nabla \log p(\mathbf{x}_t)



∇log⁡p(xt∣y)=∇log⁡p(xt)+γ(∇log⁡p(xt∣y)−∇log⁡p(xt))\nabla \log p(\mathbf{x}_t \mid y) = \nabla \log p(\mathbf{x}_t) + \gamma \left( \nabla \log p(\mathbf{x}_t \mid y) - \nabla \log p(\mathbf{x}_t) \right)
=∇log⁡p(xt)+γ∇log⁡p(xt∣y)−γ∇log⁡p(xt)= \nabla \log p(\mathbf{x}_t) + \gamma \nabla \log p(\mathbf{x}_t \mid y) - \gamma \nabla \log p(\mathbf{x}_t)
=γ∇log⁡p(xt∣y)⏟conditional score+(1−γ)∇log⁡p(xt)⏟unconditional score= \underbrace{\gamma \nabla \log p(\mathbf{x}_t \mid y)}_{\text{conditional score}} + \underbrace{(1 - \gamma) \nabla \log p(\mathbf{x}_t)}_{\text{unconditional score}}

profile
이의찬
Data Science
이전 포스트

Denoising diffusion probabilistic models(neurIPS_2020)

0개의 댓글