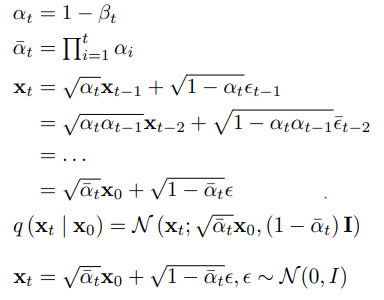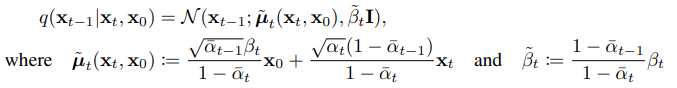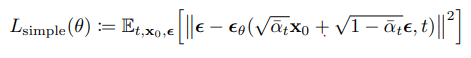DDPM

Forward process
-
forward process는 이전 단계(Xt−1) 기준으로 다음 단계(Xt)에 noise를 추가하는 과정
-
이 과정을 Markov process로 진행하게 되는데 Markov process란 다음 state가 현재 state에만 의존하는 형태이다.
-
forward process: q(Xt∣Xt−1) = N(xt;1−βtxt−1,βtI)
-
Xt = 1−βtXt−1 + βtϵ, ϵ ~N(0, I)
-
이때, 더해지는 noise는 미리 정해둔 noise schedule β를 사용
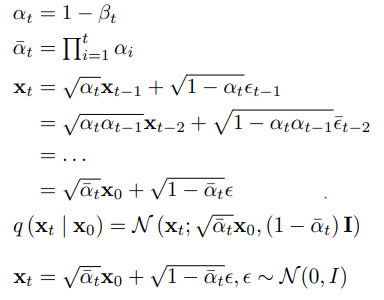
Reverse process
- Reverse process는 forward process와 반대로 noise를 제거하는 과정
-
Reverse process: pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))
-
즉, Xt에서 Xt−1로 갈 때 분포의 평균을 학습하는 것이 Reverse process
Loss
-
L = maxlog(pθ(x))
-
Maximize log likelihood는 untractable
-
Loss를 Variational Lower Bound 사용
-
Variational Lower Bound는 모든 구간에 대해서 실제 likelihood 보다 작도록 설정
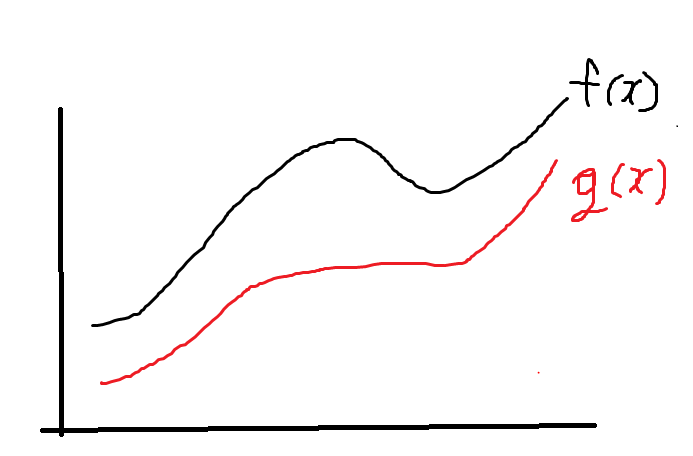

Eq[DKL(q(xT∣x0)∥p(xT))+t>1∑DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))−logpθ(x0∣x1)]
prior matching term
DKL(q(xT∣x0)∥p(xT))
- forward process를 진행 할 때, 사전에 정의한 분포와 유사하도록 minimize KL-divergence
- forward process를 가우시안 분포로 가정했기 때문에 상수취급 가능
reconstruction term
logpθ(x0∣x1)
- 마지막 이미지로 갈 때 maximize log likelihood
- 비중이 작기 때문에 상수취급 가능
Denoising term
∑t>1DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))
DKL(q(xt−1∣xt)∥pθ(xt−1∣xt))
q(xt−1∣xt)를 모른다는 문제가 있지만, X0을 conditioning 하여 전개하면 계산 가능
- 이때, reverse process를 Markov process로 정의했기 때문에 X0을 conditioning해도 정의가 깨지지 않음
q(xt−1∣xt,x0)는 Bayes Rule로 계산 가능
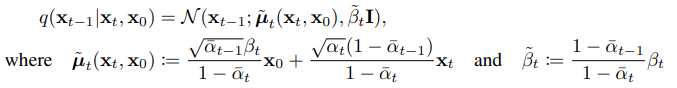
즉, X0(원본 이미지)와 Xt가 있을 때 Xt−1은 평균이 μ~t=αt1(xt−1−αˉt1−αtϵt), 분산이 β~t=1−αˉt1−αˉt−1⋅βt인 가우시안을 따른다라고 해석 할 수 있음
model이 평균이 μ~t이고 분산이 β~t인 가우시안 분포를 학습
최종적으로 q(xt−1∣xt,x0)와 Model이 예측한 분포 pθ(xt−1∣xt)가 최대한 비슷하도록 학습
이때, 정답 분포의 평균과 분산중 미지수는 ϵ만 있기 때문에 모델은 ϵ만 예측하면 되고
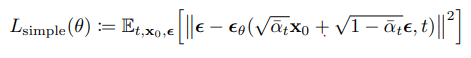

참고