Lecture 7 : Tree

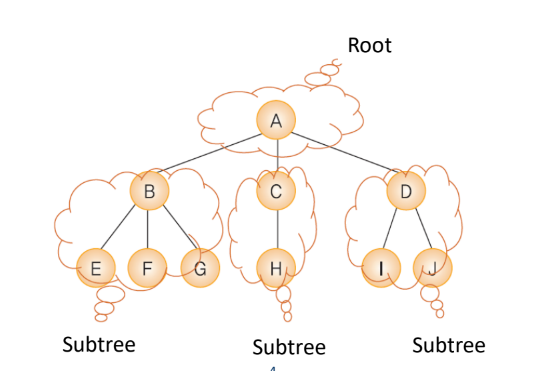
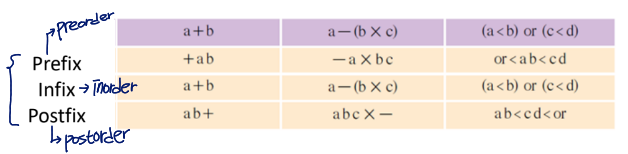Tree : Data structure representing a hierarchical structure

Note) Lists, stacks, and queues are linear structures

• Tree consisits of nodes of parent-child relationship
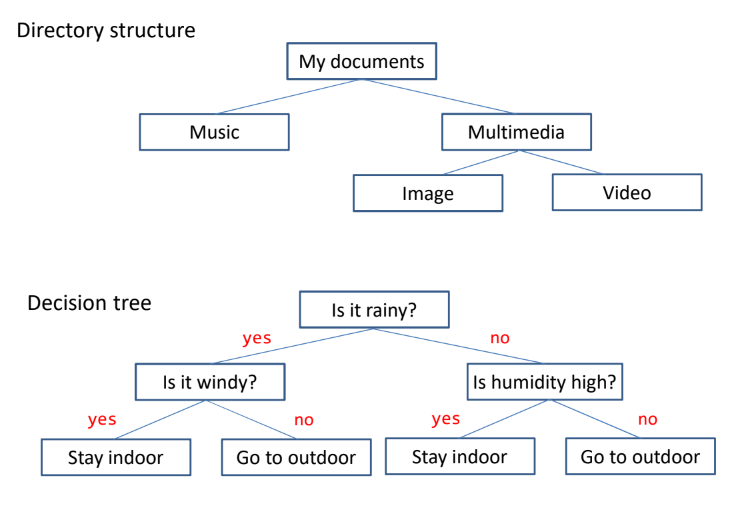
• Applications
  • Directory structure of computer disks
  • Decision tree in artificial intelligence

Terminology

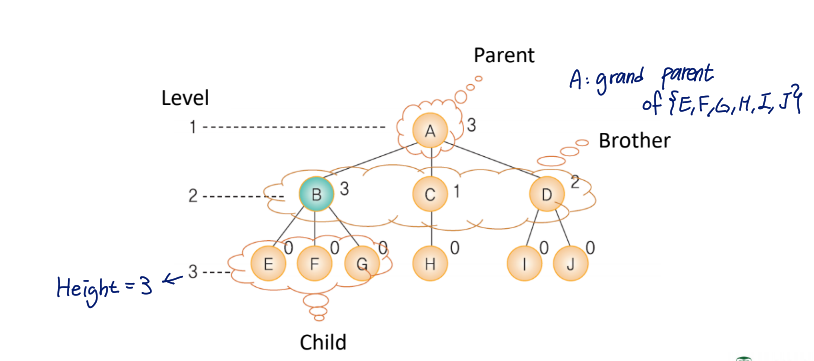
1. node: tree component
2. root: node without parents
3. subtree: consists of one node and its descendants
4. terminal node: node without childern
   leaf node랑 같은 개념인듯
5. non-terminal node: node with at least one child
   
6. level: the number of each layer in the tree
7. height: the maximum level of the tree
8. ancestor: parent, grandparent
9. offspring node: child, grandchild
   

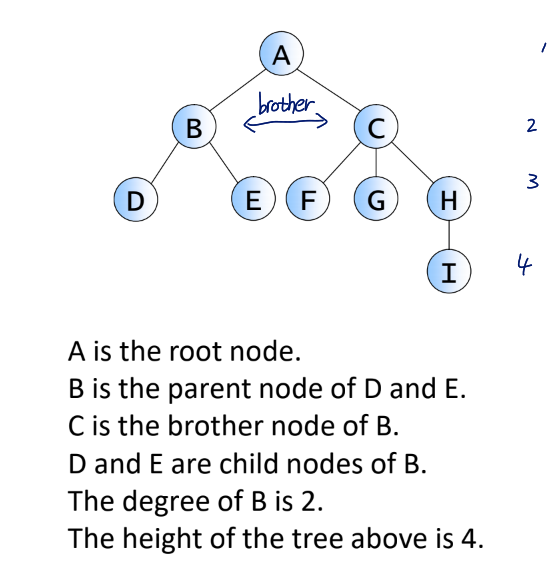
Example

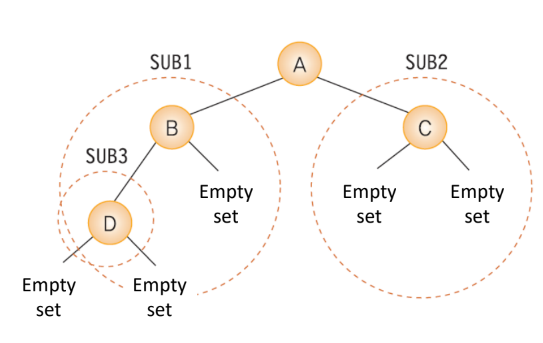
Tree Type

1. Binary tree
2. General tree

Binary tree

A tree in which all nodes have at most two subtrees

• up to two child nodes exist in a node
• the degree of all nodes is 2 or less → easy to implement
• there is an order between the subtrees(left and right)
• is either an empty set or a finite set of nodes consisting of a root, a left subtree, and a right subree
• the subtrees of the binary tree should be binary trees

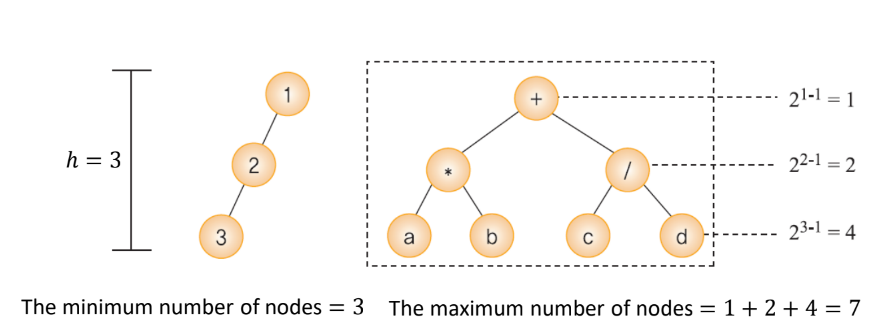
For a binary tree of height n,

n <= # of nodes <= 2ⁿ- 1
→ [log₂(m+1)] <= height of binary tree <= m
m = number of nodes

Types

1. full binary tree
2. complete binary tree
3. other binary tree
   

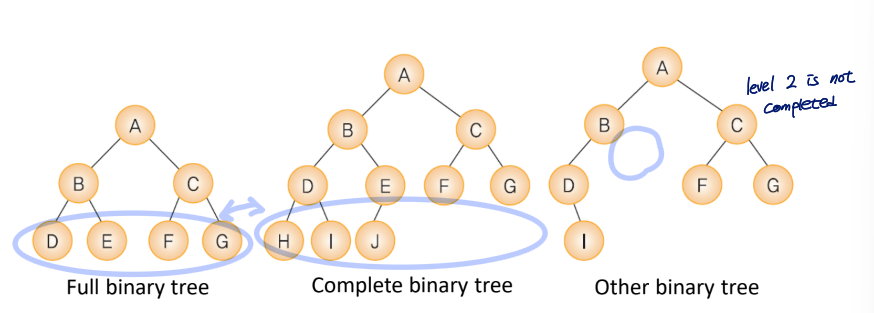
Full Binary Tree

binary tree which is full of nodes at each level of the tree

# of nodes: (i = 0부터 k-1까지)∑2^i = 2^k - 1
k = level of tree

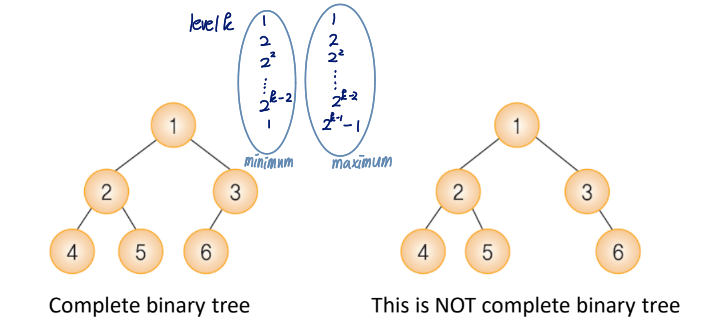
Complete Binary Tree

• levels 1 to level k-1 are filled with nodes
• at last level k, nodes are filled in order from left to right

Note) the node number is identical to that of full binary tree

Binary Tree using Array

• Assumtion: all binary trees are a full binary tree
• each node is numbered and its number is used as an index of the array to store the node's data in the array

- Pros: easy to implement
- Cons: wastes memory spaces, except for full or complete binary trees
full or complete binary tree에서 효과적인 방법

Index of parent and child

• Parent node of node i: i/2
• Left child node of node i: 2i
• Right child node of node i: 2i + 1

Binary Tree using Linked List

using a pointer, a parent node points a child node
connection이 2개가 된 것 말고는 simple linked list와 같음

Code

typedef struct TreeNode{
	int data;
    struct TreeNode *left, *right;
}TreeNode;

//       n1
//     /  |
//   n2  n3

void main(){
	TreeNode *n1, *n2, *n3;
    
    n1 = (TreeNode *)malloc(sizeof(TreeNode));
    n2 = (TreeNode *)malloc(sizeof(TreeNode));
    n3 = (TreeNode *)malloc(sizeof(TreeNode));
    
    n1->data = 10;
    n1->left = n2;
    n1->right = n3;
    
    n2->data = 20;
    n2->left = NULL;
    n2->right = NULL;
    
    n3->data = 10;
    n3->left = NULL;
    n3->right = NULL;
}

Traversal of Binary Tree

Traversal

visiting all nodes of the tree
recursion을 사용하여 진행할 예정

1. Preorder traversal: V(Root) -> L -> R

the root node is visited before child nodes(L/R)

2. Inorder traversal: L -> V -> R

visit in an order of left descendant, root, right dexcendant

3. Postorder traversal: L -> R -> V

child nodes(L/R) are visited first from the root node

Preorder Traversal

Procedure

1. visit the root node
2. visit the left subtree
3. visit the right subtree

맨왼쪽의 child까지 왼쪽으로 진행하며 traversal하는 방식

Pseudo code

preorder(x)
if x != NULL
	print Data(x);
    preorder(LEFT(x));
    preorder(RIGHT(x));

Call order of preorder traversal

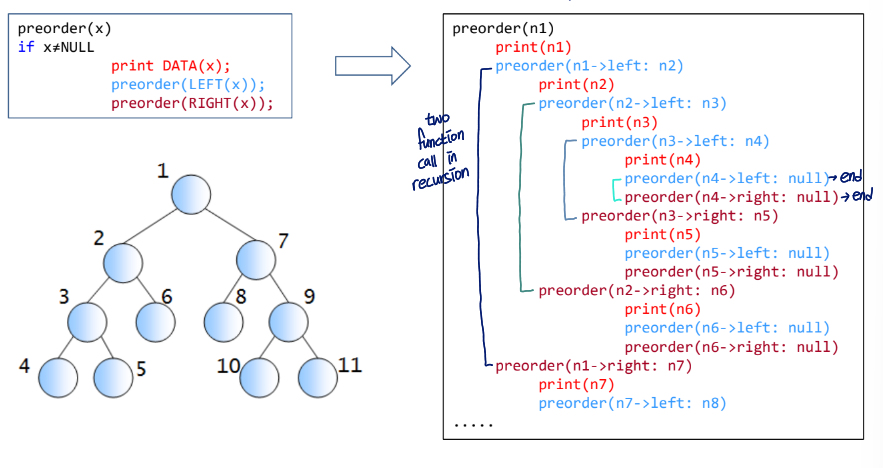
stack의 형태

Example

Output of structured documents(non-binary tree)

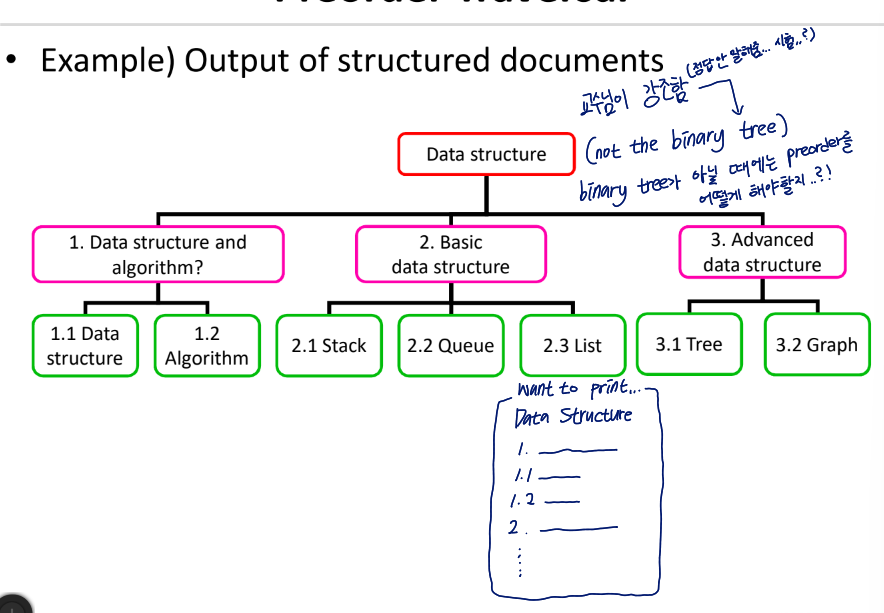
지저분하구먼,,

binary tree가 아닐 때에는 preorder를 어떻게 해야할까?
child 노드에 맨 왼쪽부터 순서를 매긴 데이터?를 추가해서 순서대로 하도록 해야되지 않을까?

Inorder Traversal

Procedure

1. visit the left subtree
2. visit the root node
3. visit the right subtree

subtree 단위로 올라가며 데이터 출력, left-most node will be printed out first

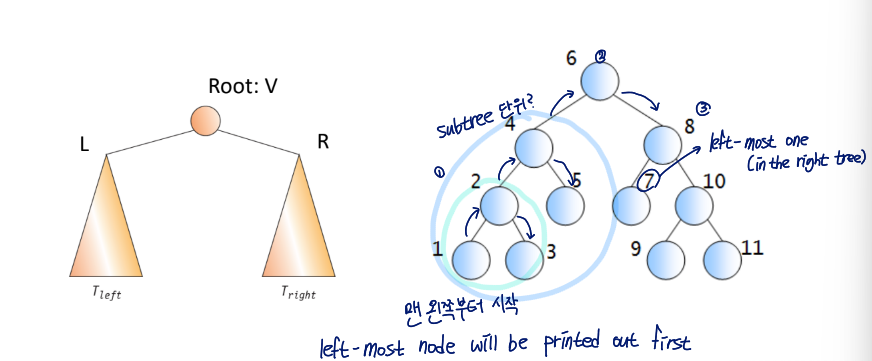
Pseudo code

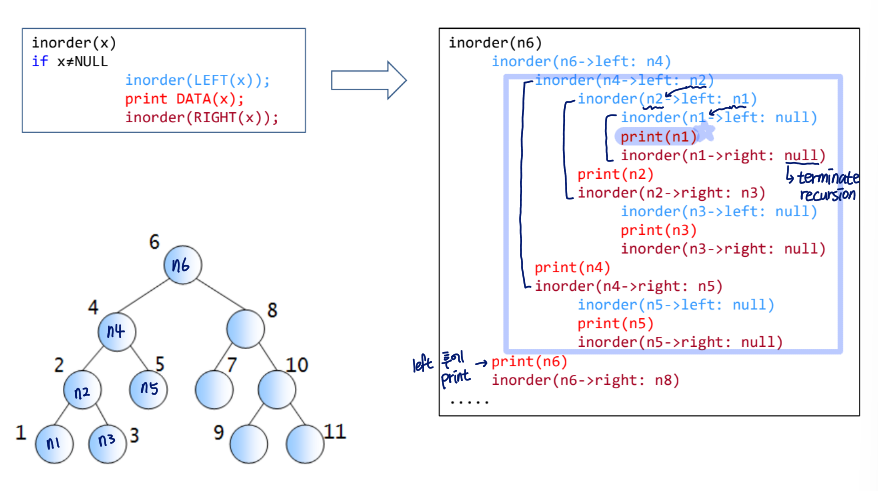
inorder(x)
if x != NULL
    inorder(LEFT(x));    //inorder left recall 후 print own data
    print Data(x);
    inorder(RIGHT(x));

Call order of inorder traversal

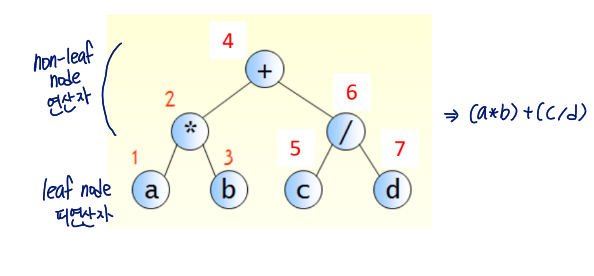
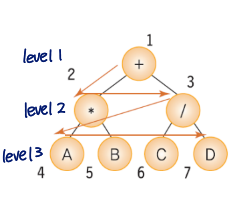
Example

formula tree: non-leaf node = operator, leaf node = operand

Postorder Traversal

Procedure

1. visit the left subtree
2. visit the right subtree
3. visit the root node

Pseudo code

postorder(x)
if x != NULL
    postorder(LEFT(x));    
    prostrder(RIGHT(x));
    print Data(x);

Call order of postorder traversal

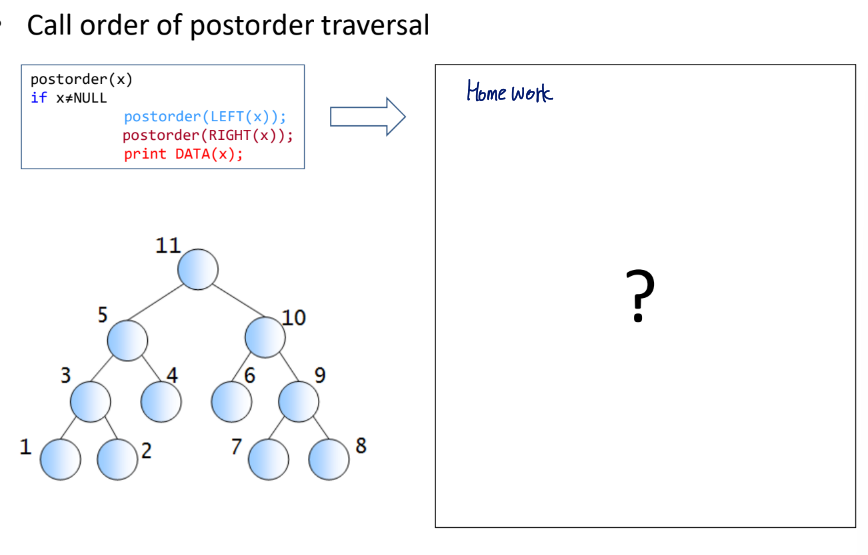
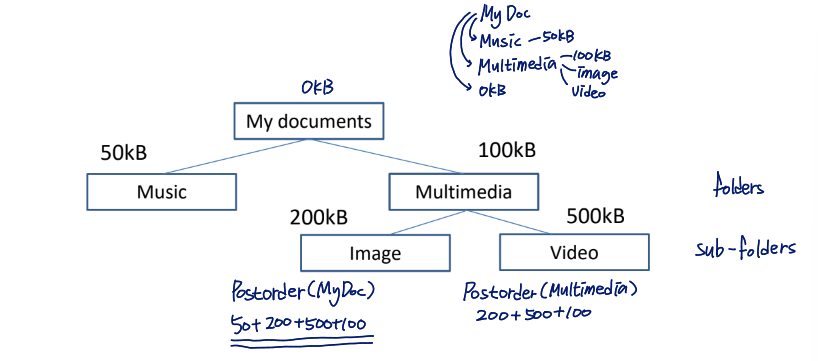
Example

calculation of directory size
binary postorder traversal과 약간 다름

Example Code of Traversals

typedef struct TreeNode{
	int data;
    struct TreeNode *left, *right;
}TreeNode;

//             15(n6)				    level1
//      4(n2)          20(n5)			level2
// 1(n1)          16(n3)     25(n4)		level3

TreeNode n1 = {1, NULL, NULL};
TreeNode n2 = {4, &m1, NULL};
TreeNode n3 = {16, NULL, NULL};
TreeNode n4 = {25, NULL, NULL};
TreeNode n5 = {20, &n3, &n4};
TreeNode n6 = {15, &n2, &n5};

preorder(TreeNode *root){
	if(root) {
    	printf("%d\n", root -> data);
        preorder(root->left);
        preorder(root->right);
    }
}

inorder(TreeNode *root){
	if(root) {
        inorder(root->left);
        printf("%d\n", root -> data);
        inorder(root->right);
    }
}

postorder(TreeNode *root){
	if(root) {
        postorder(root->left);
        postorder(root->right);
        printf("%d\n", root -> data);
    }
}

void main(){
	inorder(root);
    preorder(root);
    postorder(root);
}

Level Traversal

method for visiting each node in order of level
zig-zag scan을 떠올리면 될듯!

Use queue, whereas conventional traversal methods use stack

Pseudo Code

level_order(root)

initialize queue;
if(root == NULL) then return;
enqueue(queue, root);
while is_empty(queue) != TRUE do
	x ← dequeue(queue);
    if(x->left != NULL)
    	enqueue(queue, LEFT(x));
    if(x->right != NULL)
    	enqueue(queue, RIGHT(x));

C Code

1. 시작 전 tree 생성

typedef struct TreeNode{
	int data;
    struct TreeNode *left, *right;
}TreeNode;

//             15(n6)				    level1
//      4(n2)          20(n5)			level2
// 1(n1)          16(n3)     25(n4)		level3

TreeNode n1 = {1, NULL, NULL};
TreeNode n2 = {4, &m1, NULL};
TreeNode n3 = {16, NULL, NULL};
TreeNode n4 = {25, NULL, NULL};
TreeNode n5 = {20, &n3, &n4};
TreeNode n6 = {15, &n2, &n5};
TreeNode *root = &n6;

typedef TreeNode* element;
typedef struct QueueNode {
	element item;
    struct QueueNode* link;
}QueueNode;

typedef struct QueueType{
	QueueNode* front;
    QueueNode* rear;
}QueueType;

2. level traversal 함수 정의 뒤 실행

void level_order(TreeNode *ptr){
	QueueType q;
    
    init(&q);
    if(ptr == NULL) return;
    
    enqueue(&q, ptr);
    while(!is_empty(&q)){
    	ptr = dequeue(&q);
        printf("%d\n", ptr->data);
        if(ptr -> left)
        	enqueue(&q, ptr->left);
        if(ptr->right)
        	enqueue(&q, ptr->right);
    }
}

void main(){
	printf("level traversal\n")
    level_order(root);
    printf("\n");
}

Formula Tree

represents an arithmetic equation as tree

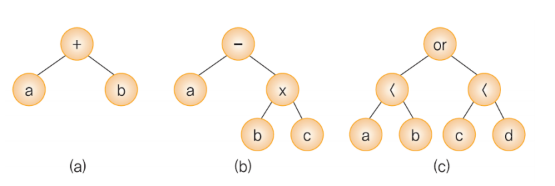
• Non-terminal node: operator
• Terminal node: operand

• Preorder traversal → prefix
• Inorder traversal → infix
• Postorder traversal → postfix
  

Calculation of formula tree

• using postorder traversal
• calculate the value of the subtree as a recursive call
• when visiting a non-terminal node, the values of both subtrees are calculated using the operator stored in the node

pseudo code

evaluate(exp)
1. if exp = NULL
2. 		then return 0;
3. if exp->left = NULL and exp->right = NULL
4. 		then return exp->data;
5. x<-evaluate(exp->left);
6. y<-evaluate(exp->right);
7. op <- (exp->data);
8. return (x op y);

c code

TreeNode n1 = {1, NULL, NULL};
TreeNode n2 = {4, NULL, NULL};
TreeNode n3 = {'*', &n1, &n2};
TreeNode n4 = {16, NULL, NULL};
TreeNode n5 = {25, NULL, NULL};
TreeNode n6 = {'+', &n4, &n5};
TreeNode n7 = {'+', &n3, &n6};
TreeNode *exp = &7;
//			+
//		*		+
//	1	  4	 16    25

int evaluate(TreeNode *root){
	if(root == NULL)
    	return 0;
    if(root->left == NULL && root->right == NULL)
    	return root->data;
    else{
    	int op1 = evaluate(root->left);
        int op2 = evaluate(root->right);
        switch(root->data){
       	case '+': return op1+op2;
        case '-': return op1-op2;
        case '*': return op1*op2;
        case '/': return op1/op2;
        }
    }
    return 0;
}

void main(){
	printf("%d", evaluate(exp));
}

Calcuation of Directory Size

using postorder traversal

int calc_dir_size(TreeNode *root){
	int left_size, right_size
    if(root){
    	left_size = calc_dir_size(root->left);
        right_size = calc_dir_size(root->right);
        return(root->data + left_size + right_size);
    }
    return 0;
}

directory size of left and right subtrees를 각각 구한 다음에 루트의 크기와 함께 더하여 사이즈를 구하는 방식

Binary Tree Operation

Key Idea

• 하나의 복잡한 문제를 나눠서 반복적으로 구하도록 함
• 초기치 설정 중요

Number of Nodes

• calculate the number of nodes in the tree
• recursively calls each subtree, adds 1 to the returned value, and returns

int get_node_count(TreeNode *node){
	int count = 0;		
    if(node != NULL){
    	count = 1 + get_node_count(node->left) + get_node_count(node->right);
    }
    return count;
}

Number of Leaf Nodes

int get_leaf_count(TreeNode* node){
	int count = 0;
    if(node != NULL){
    	if(node->left == NULL && node->right == NULL)
        	return 1;
        else
        	count = get_leaf_count(node->left) + get_leaf_count(node->right);
    }
    return count;
}

Height

recursive call to the subtree, and returns the maximum value among the return values of the subtrees

int get_height(TreeNode *node){
	int height = 0;
    if(node != NULL){
    	height = 1 + max(get_height(node->left), get_height(node->right));
    }
    reuturn height;
}

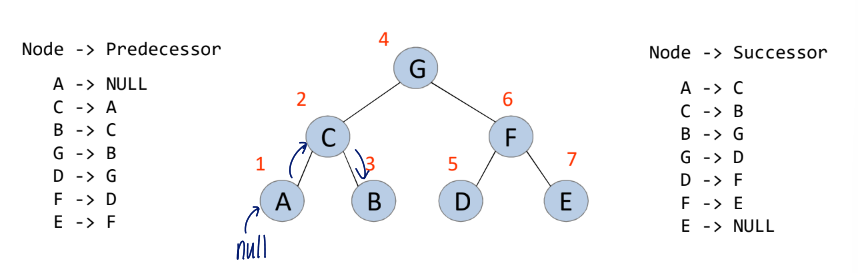
Predecessor/Successor in Binary Tree

defined depending on the type of traversal

Example
1. inorder predecessor: previous node at the inorder traversal
2. inorder successor: next node at the inorder traversal

Find the successor in the inorder traversal

Case 1. have right child
Case 2. have no right child
pseudo code

Tree_successor(x){
	if x->right != NULL
    	return the leftmost node of right subtree
    
    y = x->parent
	while(y!=NULL and x==y->right){
    	x = y;
        y = y->parent;
    }
    return y;
}

만약 부모가 자식의 successor가 아닌 경우는 부모의 부모, 혹은 그 이상의 부모노드가 successor가 될 것임

Threaded Binary Tree

• Problem of recursive traversal in binary tree
  • Recursive calls may be time-consuming for large scale tree

To address the above issue, we can use the successor

Threaded binary tree

• saves the successor in the NULL link for traversal
• without recursive calls, we can traverse the nodes of the tree

leaf node의 null(unused memory)를 own successor's address로 채움 → 기존의 메모리를 사용하여 낭비가 발생하지 않음 + compute become simple

Example) inorder traversal
1. in the leaf nodes, their successors are stored in the right links(which are originally NULL)
2. 맨마지막 노드는 successor 없음
3. right links of the nodes가 null이 아니므로 leaf nodes의 successor를 빠르게 찾을 수 있음

'is_thread'

To distinguish whether the links of nodes indicate the inorder successor or the child

typedef struct TreeNode{
	int data;
    struct TreeNode *left, *right;
    int is_thread;	//TRUE, if right link is a thread
}TreeNode;

'find_successor'

Function that finds the inorder successor

TreeNode *find_successor(TreeNode *p){
	TreeNode *q = p->right;    //q: right pointer of p
    
    if(q==NULL || p->is_thread == true) //right subtree가 없는 경우
    	return q;					  //q==null은 예시사진의 E의 경우	  
    
    while(q->left != NULL) q = q->left;		//right subtree가 있는 경우
    return q;
}

이전의 inorder successor 구할 때보다 계산량이 줄어듦

Iterative inorder traversal function using thread

Inorder traversal은 가장 왼쪽의 노드에서 시작하기 때문에 먼저 leftmost node를 찾아야됨

void thread_inorder(TreeNode *t){
	TreeNode *q;
    q = t;
    while(q->left) q = q->left;
    
    do{
    	printf("%c", q->data);
        q = find_successor(q);	//call the successor
    } while(q);
}

Example code

그냥 위의 코드들 모아놓은 거..!

typedef struct TreeNode{
	 int data;
     struct TreeNode *left, *right;
     int is_thread;
}TreeNode;

//			G
//    C			 F
//  A   B      D    E
TreeNode n1 = {'A', NULL, &n3, 1};
TreeNode n2 = {'B', NULL, &n7, 1};
TreeNode n3 = {'C', &n1, &n2, 0};
TreeNode n4 = {'D', NULL, &n6, 1};
TreeNode n5 = {'E', NULL, NULL, 0};
TreeNode n6 = {'F', &n4, &n5, 0};
TreeNode n7 = {'G', &n3, &n6, 0};
TreeNode *exp = &n7;


TreeNode *find_successor(TreeNode *p){
	TreeNode *q = p->right;    //q: right pointer of p
    
    if(q==NULL || p->is_thread == true)
    	return q;			  //right subtree가 없는 경우
    
    while(q->left != NULL) q = q->left;		//right subtree가 있는 경우
    return q;
}

void thread_inorder(TreeNode *t){
	TreeNode *q;
    q = t;
    while(q->left) q = q->left;
    
    do{
    	printf("%c", q->data);
        q = find_successor(q);	//call the successor
    } while(q);
}

void main(){
	n1.right = &n3;
    n2.right = &n7;
    n4.right = &n6;
    
    thread_inorder(exp);
}

Binary Search Tree(BST)

Data structure for efficient search operation

key(left subtree) <= key(root node) <= key(right subtree)

Can get sorted values in ascending order throught the inorder traversal!

Search Operation in Binary Search Tree

Three cases

1. If the results are the same, the search ends successfully
2. If the given value < the value of the root node, the search restarts for the left child of this root node
3. If the given value > the values of the root node, the search restarts for the right child of this root node

pseudo code

search(x, k)  //x: root node, k: given value(찾고 싶은 수)

if x == NULL
	then return NULL;
if k = x->key
	then return x;
else if k<x->key
	then return search(x->left, k);	
else return search(x->right, k);

C code

1. Recursion

TreeNode *search(TreeNode *node, int key){
	if(node == NULL) return NULL;
    
    if(key == node->key) return node;
    
    else if(key < node->key) 
    	return search(node->left, key);
        
    else
    	return serach(node->right, key);
}

2. Iteration

TreeNode *search(TreeNode *node, int key){
	while(node != NULL){
    	if(key == node->key) return node;
        else if(key < node->key)
        	node = node->left;
        else 
        	node = node->right;
    }
    return NULL;
}

Insertion in Binary Search Tree

BST에서 insertion을 수행하려면, 먼저 search를 하는 것이 필요함

• BST should not contain the node with the same key value
• location where the search failed is the location where the new node is inserted
  서치가 실패한 위치(null로 뜬 부분)가 새로운 노드가 삽입될 구간

pseudo code

insert_node(T, z) //T:tree, z:element

p <- NULL;
t <- root;
while(t!=NULL) do
	p<-t;
    if z->key < p->key
    	then t<- (p->left);
    else t<- (p->right);
    
n <- make_node(key);

if p==NULL			//if tree is empty
	then root<-n;
else if z->key < p->key;
	then p(->left) <- n;
else (p->right) <- n;

C code

insert_node(TreeNode **root, int key) {
	TreeNode *p, *t;	//p: parent, t: current node
    TreeNode *n 		//new node
    t = *root;
    p = NULL;
    
    //search first
    while(t != NULL){
    	if(key == t->key){
        	printf("the same key exists in the tree\n");
            return;
        }
        p = t;
        if(key < t->key) t = t->left;
        else t = t->right;
    }
    
    n = (TreeNode*)malloc(sizeof(TreeNode));
    if(n==NULL) return;
    n->key = key;
    n->left = n->right = NULL;
    
    if(p != NULL){
    	if(key < p->key)
        	p->left = n;
        else p->right = n;
    }
    else *root = n;
}

Deletion in Binary Search Tree

Three cases

1. the node to be deleted is a leaf node
2. the node to be deleted has only one left or right subtree
3. the node to be deleted has both subtrees

Case 1

부모노드를 찾아서 연결 끊어버리기

Case 2

자식노드를 node to be deleted의 자리로 옮기기

Case 3

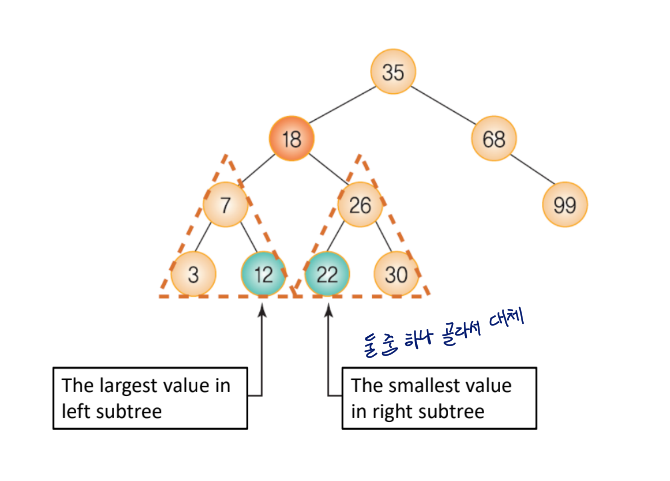
predecessor or successor를 deleted node의 위치로 옮기기

예시) 18을 없애는 경우

C code

void delete_node(TreeNode **root, int key){
	TreeNode *p, *child, *succ, *succ_p, *t;
    
    p = NULL;
    t = *root;
    while(t != NULL && t->key != key){
    	p = t;
        t = (key < t->key)? t->left: t->right;
    }
    
    if(t==NULL){
    	printf("key is not int the tree");
        return;
    }
    
    //CASE 1
    if((t->left == NULL) && (t->right == NULL)){
    	if(p!=NULL){
        	if(p->left == t)
            	p->left = NULL;
            else p->right = NULL;
        }
        else *root = NULL;  //tree에 노드가 한 개만 있는 경우
    }
    
    //CASE 2
    else if((t->left == NULL) || (t->right == NULL)){
    	child = (t->left!=NULL)? t->left: t->right;
        if(p != NULL){
        	if(p->left == t)
            	p->left = child;
            else p->right = child;
        }
        else *root = child;		//child가 하나인 루트노드 지우는 경우
        						//예시 그림 밑에 첨부
    }
    
    //CASE 3
    else{
    	//이 코드에서는 successor로 대체함, predecessor도 사용가능!
    	succ_p = t;		//successor의 부모도 찾아야 함(connect 변경때문)
        succ = t->right;
        while(succ->left != NULL){
        	succ_p = succ;
            succ = succ->left;
        }
        
        //successor : leftmost node in right subtree이기 때문에
        //left child를 가지고 있지 않음
        // => right child가 있는 경우와 아닌 경우만 고려하면 됨
        if(succ_p->left == succ)
        	succ_p->left = succ->right;
        else
        	succ_p->right = succ->right;
            
        t->key = succ->key;
        t = succ;
    }
    //free(t);
}

Performance Analysis in Binary Search Tree

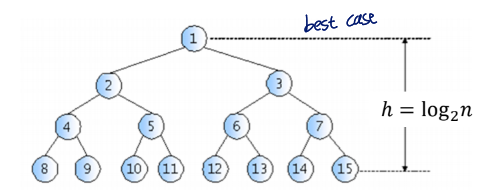
The time complexity of the search, insertion, and deletion in the binary search tree is proportional to the tree height h

Time Complexity = O(h)

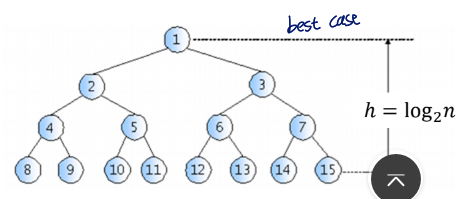
• the best case : the binary tree is balanced
  h = log₂n
  
• the worst case : for one-sided, oblique binary trees
  h = n
  
  → the time complexity are the same as that of sequential search

n개의 data로 다양한 BST를 만들 수 있기 때문에 best case의 BST로 만들기 위해 노력해야함