Photometric Stereo

Introduction

$\text{Image Intensity} = F(\text{Source, Surface Normal, Surface Reflectance})$

• Known
  • Image Intensity
  • Source
  • Surface Reflectance
    BRDF와 같은 방법들을 통해 알아낼 수 있음
• Unknown
  • Surface Normal

Photometric stereo

여러 sources를 사용하여 측정된 image intensities를 통해 3차원의 shape information을 recover하는 방법

이렇게 각각 다른 각도에서 빛을 받은 물체의 사진을 찍고, 이 사진들을 통해 3D shape을 뽑아냄

Gradient Space and Reflectance Map

Surface Gradient and Normal

Let $z=f(x,y)$ represent a 3D surface

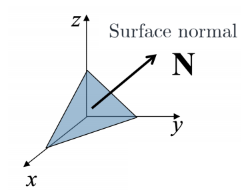
이때, z axis에서 image를 capture한다고 가정

• Equation of plane(평면 방정식)
  $Ax+By+Cz+D=0 \\ \text{or} \quad \frac{A}{C}x+\frac{B}{C}y+z+\frac{D}{C}\\\text{or}\quad z = -(\frac{A}{C}x+\frac{B}{C}y+\frac{D}{C})$

• Let $-\frac{\partial z}{\partial x} = \frac{A}{C}=p \quad-\frac{\partial z}{\partial y} = \frac{B}{C} = q$

• Surface normal
  $N = \big(\frac{A}{C}, \frac{B}{C},1\big) = (p,q,1)$

• Unit surface normal
  $n=\frac{N}{|N|}=\frac{(p,q,1)}{\sqrt{p^2+q^2+1}}$

Gradient Space

z plane은 Gradient Space로 불림 ($pq$ plane으로도 불림)

• 그 위의 각 점들은 모두 particular surface orientation과 일치함

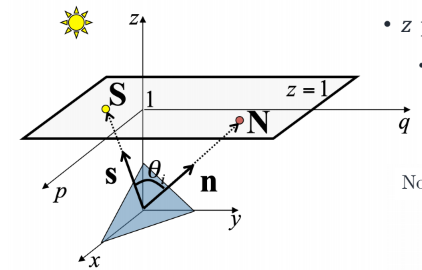
• z=1인 평면이 z plane
• 평면에서 수직으로 나오는 벡터가 surface normal(N)
• surface normal과 방향은 같고 크기를 1로 한 벡터 : unit surface normal(n)
• $\cos\theta_i = n\cdot s=\frac{(pp_s+qq_s+1)}{\sqrt{p^2+q^2+1}\sqrt{p_s^2+q_s^2+1}}$
  • normal vector
    $n = \frac{N}{|N|} = \frac{(p,q,1)}{\sqrt{p^2+q^2+1}}$
  • source vector
    $s = \frac{S}{|S|} = \frac{(p_s,q_s,1)}{\sqrt{p_s^2+q_s^2+1}}$

Reflectance Map

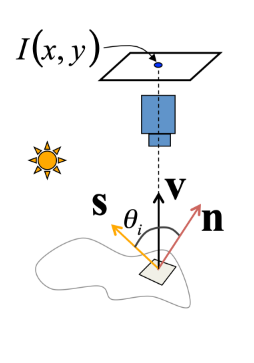
source direction $s$, surface reflectance가 주어졌을 때, image intensity(irradiance) at a point (x,y)는
$\text{Reflectance map: } I = R(p,q)$
surface에 대한 정보 추가로 필요

Reflectance Map: Lambertian Surface

Image Intensity

Lambertian surface의 경우

• Image intensity
  $I = \frac{\rho}{\pi}kc\cos\theta_i=\frac{\rho}{\pi}kcn\cdot s$
  • $k$: source brightness (radiance intensity)
    $L(\theta_v, \rho_v)$식에서의 $I$
  • $\rho$: surface albedo (reflectance)
  • $c$: normalization constant (camera gain)

$\frac{\rho}{\pi}kc=1$이라고 하면, $I=\cos\theta_i=n\cdot s$
→ Lambertian의 경우에는 angle만 intensity에 영향을 미치는 것을 알 수 있음

$I = \cos\theta_i=n\cdot s = \frac{(pp_s+qq_s+1)}{\sqrt{p^2+q^2+1}\sqrt{p_s^2+q_s^2+1}} = R(p,q)$

• $R(p,q)$ : Reflectance Map of Lambertian

Iso-brightness contour

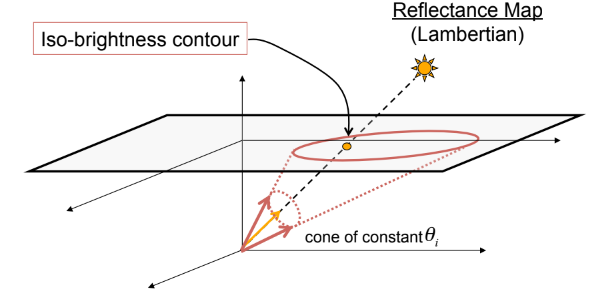
z plane에 있는 저 원 위의 점들은 $\theta_i$의 값이 모두 같음
→ 저 unit vector들은 모두 같은 brightness를 가짐 : Iso-brightness contour

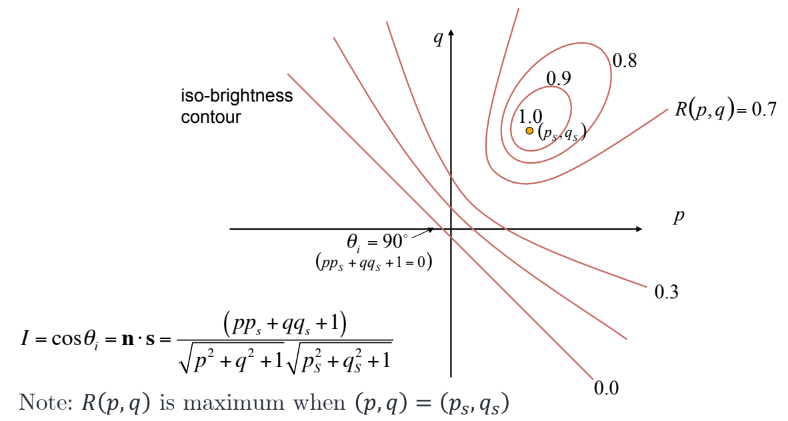
• $I=0$이 되는 경우: $\theta=\frac{\pi}{2}$
• $I=0$이 되는 line 밑의 영역은 모두 0의 값을 지니게 됨

빛이 어디서 빛추는지에 따라 iso-brightness countour는 다르게 나타남

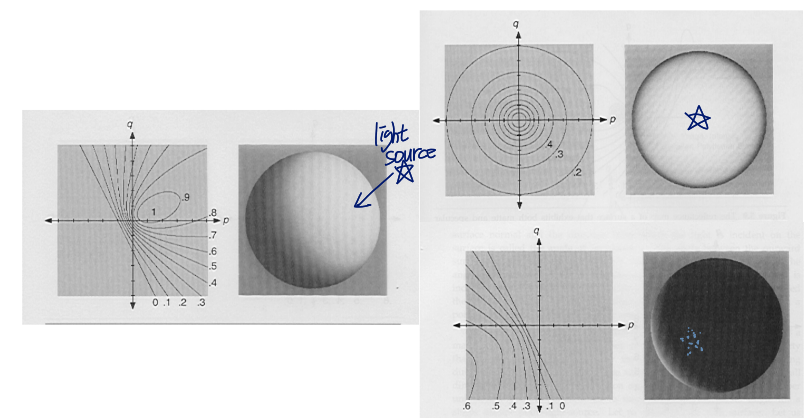
그러면 만약...

• source direction $(p_s,q_s)$
• surface reflectance $\rho$
• one image irradiance image $I(x,y)$

들이 주어졌을 때, unique surface orientation $(p,q)$를 구할 수 있을까?

아니오

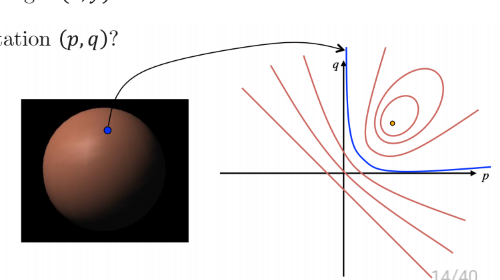
위에서의 주어진 정보들을 통해 주어진 구에서 저 point가 iso-contour에서 특정 곡선 위에 있다는 것을 알 수 있음
그러나 저 line 위의 수많은 points 중 정확히 어떤 게 저 point의 surface orientation인지는 알 수 없음

Photometric Stereo

Idea

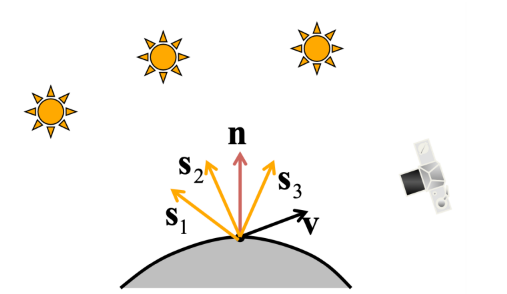
different lighting의 밑에서 촬영한 여러 이미지들을 통해 surface orientation의 모호성을 해결하고자 함

Photometric Stereo

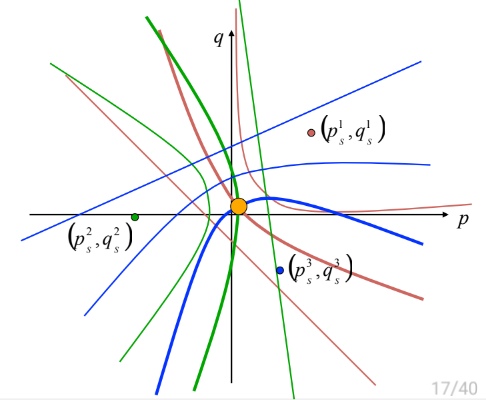
multiple images의 iso-contours에서 각각의 접점을 $(p,q)$로 채택

구하는 방법

1. N images with N known light sources 필요
2. known source direction과 BRDF를 통해, 각 source direction의 reflectance map 생성
3. 각 픽셀의 위치 $(x,y)$를 사용해 N curves의 intersection인 $(p,q)$를 찾음
   이때 $(p,q)$는 $(x,y)$ 픽셀의 surface normal

smallest $N$은 material properties에 따라 다름
항상 그런 건 아니지만 Lambertian의 경우, 3개로 충분
specular case에는 최악의 경우 infinite 필요

Photometric Stereo: Lambertian Case

• Image irradiance
  $I=\frac{\rho}{\pi}kc\cos\theta_i=\rho n\cdot s\quad\big(\frac{kc}{\pi} = 1\big)$
• Image irradiances under three light sources
  $\begin{cases}I_1=\rho n\cdot s_1\\I_2=\rho n\cdot s_2 \\ I_3=\rho n\cdot s_3 \end{cases}$

이 경우, matrix form으로

$\begin{bmatrix}I_1\\\\I_2\\\\I_3\end{bmatrix} = \begin{bmatrix}s_1^T\\\\s_2^T\\\\s_3^T\end{bmatrix}\rho n$
이렇게 표현 가능

• known(measured)
  • $I_{3\times 1}$
  • $S_{3\times 3}$
    • $s_i^T$: $(x,y,z)$
• unknown
  • $\tilde{n} = \rho n$

Solution

$\tilde{n} = S^{-1}I$

Albedo

$\rho=|\tilde{n}|$

Surface normal

$n=\frac{\tilde{n}}{|\tilde{n}|} = \frac{\tilde{n}}{\rho}$

그러나 S가 invertible하지 않을 때는 사용 불가
source direction이 linear combination of the other two로 되는 경우
e.g., $s_3=\alpha s_1 + \beta s_2$

N>3인 경우 더 좋은 결과를 얻을 수 있음
이때의 solution은..

• Least squares solution
  $S^TI=S^TS\tilde{n} \\ \rightarrow \tilde{n}=(S^TS)^{-1}S^TI$
  이 후에는 전과 같이 풀면 됨

Color Images

• 각 채널에 따라 three sests of equation 구하기

  • $I_R = \rho_RSn$
  • $I_G = \rho_GSn$
  • $I_B = \rho_BSn$

• simple solution: first solve for n using one channel

• then substitute known n into the above equations to get

• or combine three channels and solve for n
  $I=\sqrt{I_R^2+I_G^2+I_B^2} = \rho Sn$

Results

Lambertian Sphere

Lambertian Mask

Non-Lambertian Toy

Lambertian이 아니라 shiny part가 존재. albedo가 정확하지 않음

Calibration Based Photometric Stereo

Use calibration object of known size, shape (e.g., sphere) and same reflectance as the scene objects
calibration object에는 sphere가 사용하기 좋음

Orientation Consistency
points with the same surface normal produce the same set of intensities under different lighting

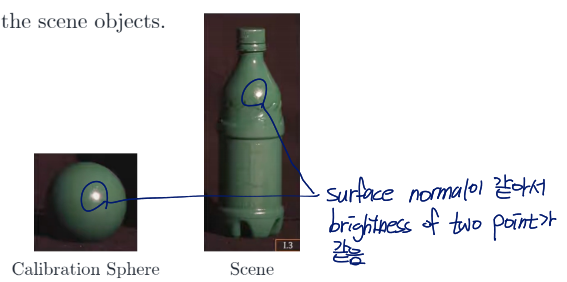
Calibration Based Photometric Strereo

1. $N\geq 3$개의 다른 light sources 밑에서 각각의 이미지 찍기
   • 구 위의 each point들은 $N$ image intensities $(I_1,I_2,...,I_N)$를 생성함
2. known size of the sphere를 사용하여 구의의 점들에 대한 surface normal $(p,q,1)$들을 구함
3. lookup table for the N-tuple 생성
   $\quad (I_1,I_2,...,I_N)\rightarrow (p,q)$
4. capture $N$ images of the scene object under the same $N$ light source
5. for each pixel in the scene, use lookup table to map $(I_1,I_2,...,I_N)\rightarrow (p,q)$

간단하게 생각하면 모든 값을 구할 수 있는 같은 성질의 물체를 이용하여 이와 비교하며 surface normal을 얻는 것
이 방법을 사용하면 BRDF fuction을 몰라도 구할 수 있게 됨

Shape from Normals

Shape From Surface Normals

surface normal들을 다 구했으면 이제 그로부터 shape을 구해야 됨

$(p,q) = \big(-\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}\big)$ 이기 때문에 그냥 적분하면 shape을 구해낼 수 있음

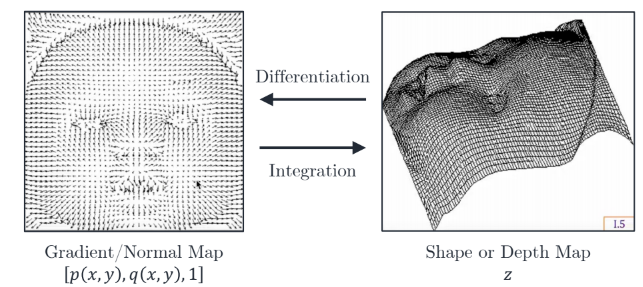
Estimate surface by intergrating surface gradient

$\quad z(x,y) = z(x_0,y_0)+\int_{x_0,y_0}^{(x,y)}-(pdx+qdy)$

where $(x_0,y_0)$ is a reference point and $z(x_0,y_0) = 0$.

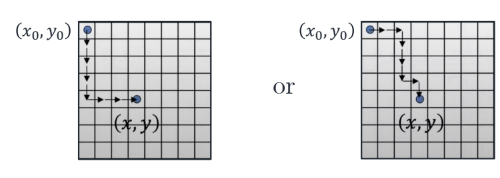
여기서 값들은 discrete하기 때문에, 적분할 때는 그냥 summation을 하면 됨
이때, 임의의 path를 설정하고 그곳에 있는 surface normal들을 합하는 것

path는 여러 종류가 가능할 수 있음

Results: Shape of Mask

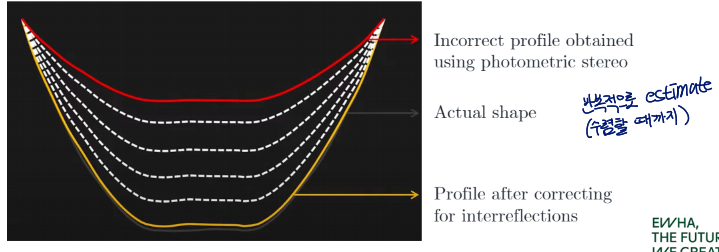
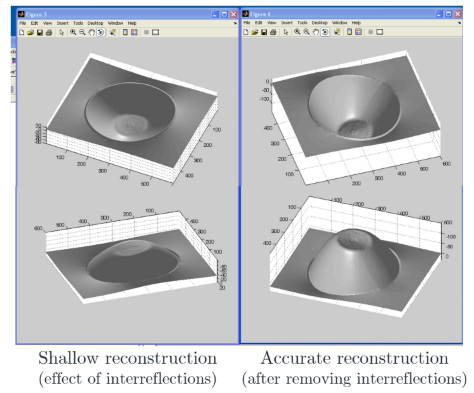
Interreflection Problem

Interreflection Problem

상호반사 문제

brightness of a scene point는 light source만 영향을 미치는 게 아니라 다른 scene points로부터의 light도 영향을 미치게 됨

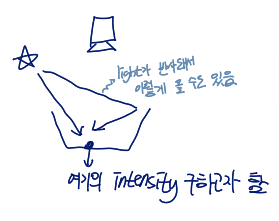
이런 식으로 다른 곳에서 반사된 빛이 영향을 미칠 수 있음

photometric stereo는 albedo를 과대평가하고, surface tilt를 과소평가함
photometric stereo overestimates albedo and underestimates surface tilt
여기서 surface tilt는 gradient of surface

이러한 문제는 interreflections를 고려하며 반복적으로 올바른 모양을 추정하면 나아질 수 있음