Radiometry and Reflectance

Light and Scene

Physics-Based Methods in Computer Vision

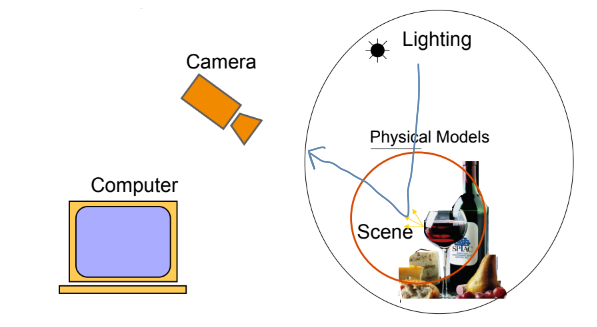
we need to understand the relation between the lighting, surface reflectance and medium and the image of the scene

Light and Shadow

shadow

light source로부터 나온 light가 물체에 의해 obstructed된 영역

그림자로 인해 computer가 물체를 인식하는 것에 문제가 발생

이 사진에서 길이 하나라는 걸 사람들은 바로 인식할 수 있지만, computer는 그림자로 인해 하나의 길이 있다는 것을 인식하기 어려워 함

그림자에 따라 물체의 보이는 색이 달라지는 것도 computer에게는 어려운 문제 중 하나

Refractions

Refraction

굴절
전달 매개의 변화로 인해 propagation of a wave의 방향이 바뀌는 현상

사람은 체크무늬(pattern)를 바로 파악할 수 있지만 computer에게는 어려움

Reflections

Reflection

반사
서로 다른 매개의 interface에서 wavefront의 방향이 바뀌어 originate한 매개로 되돌아가는 현상

computer는 유리에 비치는 물체들이 실제인 줄 앎

자율주행자동차의 경우, 길의 물웅덩이에 반사된 나무를 object로 탐지하고 멈추는 일이 발생할 수 있음

Interreflections

Interreflection

상호반사
두 reflecting surface에서 상호적인 반사가 일어나는 현상

Scattering

Scattering

산란
빛이 통과하는 매질의 국소적인 불균일성으로 인해 하나 이상의 경로에 의해 직선 궤적에서 벗어날 수밖에 없는 일반적인 물리적 과정


예를 들자면, 빛의 파장이 산란에 따라 색이 달라져서 하늘의 색이 계속 변화하는 것

More Complex Appearances

light source로 인해 머리카락이 각각 모두 다르게 보임

빛에 따라 잎의 색 다름

Radiometric Concepts

radiometric: 복사도학

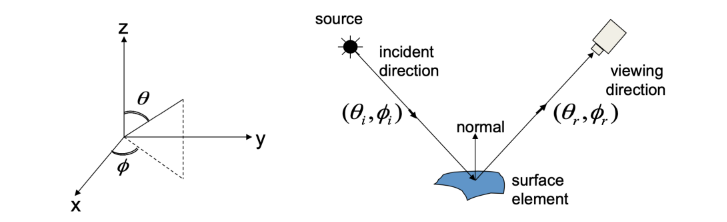
Solid Angle

3차원 공간에서의 각
solid angle is subtended by a point and a surface patch

• Angle 2D
  
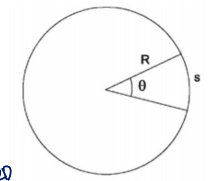
  • can be represented by a fraction of a circle's circumference
    $\theta = \frac{s}{R} \text{ (radian)}$
    (A circle has $2\pi$ radian)
• Solid angle
  
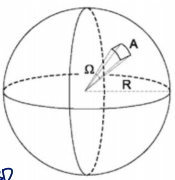
  • fraction of a sphere's area
    $\theta = \frac{A}{R^2} \text{ (steradian)}$
    (A sphere has $4\pi$ radian)

Solid Angle

$dw = \frac{dA'}{R^2} = \frac{dA\cos\theta_i}{R^2} \text{ (steradian)}$

Surface Irradiance

Light radiant flux (power) incident (received) per unit surface area
단위 표면적당 입사(수신)되는 광 복사 플럭스(전력)
간단하게 말하자면, point(surface area)에 도달하는 energy 양

• 거리가 멀어질수록 단위 면적 당 도달량이 줄어듦
• 빛이 어디서 오는지에 depend하지 않음

Surface Irradiance

$E = \frac{d\Phi_i}{dA} = \frac{\text{power}}{\text{surface area}} \text{ (watts/}m^2)$

Surface Radiance

flux emitted per unit foreshortened area per unit solid angle
small amount of surface에서 반사되는 빛의 양이라고 이해하면 될듯

• surface는 whole hemisphere로 반사될 수 있음
• L은 표면의 reflectance properties에 따라 달라짐(depend)
• L은 $\theta_r$에도 영향을 받음(depend)
  즉, surface property, 어디에서 보는지에 따라 값이 달라짐

Surface Radiance

$L = \frac{d^2\Phi_r}{(dA\cos\theta_r)dw}=\frac{\text{power}}{\text{foreshorted area x solid angle}} \text{ (watts/}m^2\text{ steradian)}$

공식 모아둔 거

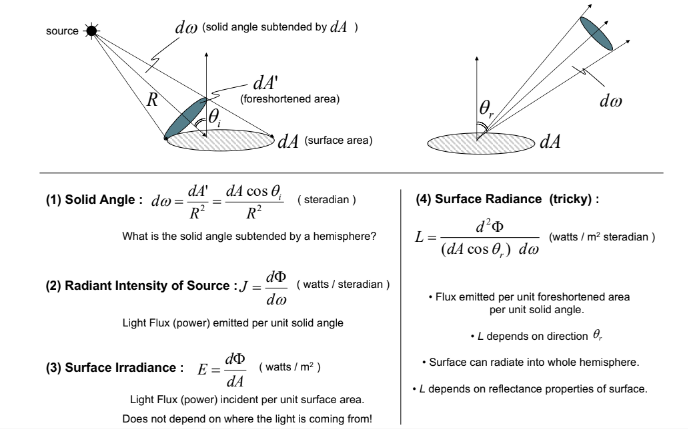
이 식들을 다 이해해야지 후에 나오는 것들도 이해할 수 있음,.

BRDF (Bi-Directional Reflectance Distribution Function)

reflectance design을 위한 mathematical modeling법

Surface Appearance

Reflectance

반사율
ratio of outgoing energy to incoming energy at a single point
incoming과 outgoing의 비율

BRDF of a surface

• given an illumination and a viewing direction
  조명과 시야의 방향이 주어짐
• a measure of how bright the surface appears
  표면이 얼마나 밝게 보이는지 측정

BRDF는 종류가 많아서 다양한 종류(형태)의 식들을 가지고 있음

BRDF

general BRDF : $f(\theta_i, \varphi_i;\theta_r,\varphi_r) = \frac{L^{surface}(\theta_r, \varphi_r)}{E^{surface}(\theta_i,\varphi_i)}$
;는 incident direction, viewing direction 순서를 구분하기 위해 사용

• $E^{surface}(\theta_i,\phi_i)$ : Irradiance at surface in direction $(\theta_i, \phi_i)$
  incoming energe
• $L^{surface}(\theta_r,\phi_r)$ : Radiance of surface in direction $(\theta_r, \phi_r)$
  outgoing energe

Important Properties of BRDFs

Conservation of Energy

$\underset{\text{hemisphere}}{\int}f(\theta_i,\varphi_i;\theta_r,\varphi_r) \leq 1$

BRDF의 적분값은 1보다 작거나 같아야 함
$\because$ 반사되는 빛의 양은 들어오는 양보다 작거나 같음
이때, $f() \geq0, L\geq0$

Helmholtz Reciprocity

열역학 제 2의 법칙 따름
reciprocity: 상호주의

$f(\theta_i,\varphi_i;\theta_r,\varphi_r) = f(\theta_r,\varphi_r;\theta_i,\varphi_i)$

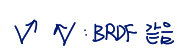
source와 viewing direction이 서로 바뀔 때, BRDF는 변화하지 않음

Common Assumption : Isotropy

Isotropy : 등방성
rotational symmetry

• BRDF는 surface가 normal에 대해서 회전할 때 변화하지 않음
  절대적으로 x,y축에서의 각도가 중요한 것은 아니라는 뜻
• can be written as a function of 3 variables: $f(\theta_i, \theta_r, \varphi_i-\varphi_r)$

그런데 이 assumption은 언제나 참인 것은 아니니까 주의하자

간단하게 이해하자면, z의 값은 유지하면서 x,y축에서 회전하면 빛이 들어오고 나가는 양의 비율은 변하지 않을 것이라는 가정

Mechanisms of Reflection

Body Reflection

• diffuse reflection으로도 불림
• matte appearance
• Non-Homogeneous Medium
• clay, paper, etc.

물질의 색을 결정하고, 내부에서 막 반사되다가 뱉어지는 특징

Surface Reflection

• specular reflection으로도 불림
• glossy appearance
• highlights
• dominant for metals

바로 반사된다는 특징

Image Intensity

$\text{Image Intensity} = \text{Body Reflection} + \text{Surface Reflection}$
image intensity는 color or something

Example Surfaces

Body Reflection

• no surface reflection
• no glossy part

Surface Reflection

• glossy
• shiny

그런데 대부분의 materials는 두 reflection을 모두 가지고 있음

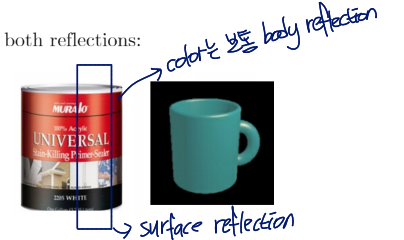
Diffuse Reflection and Lambertian BRDF

Lambertian surface

diffuse reflection을 칭하는 또다른 말

• Lambertian surface는 어느 view direction이든 똑같은 밝기(bright)로 보임
  색(intensity)도 어디서나 같음
  • outgoing directioin $\vec v$에 independent

Lambertian BRDF (simplest one)

• vision과 graphics에 자주 사용됨
• Lambertian BRDF는 각도 상관 없이 값이 일정 → constant
  $f(\theta_i,\varphi_i;\theta_r,\varphi_r) = \frac{\rho_d}{\pi}$
  • $\rho_d$ : albedo (반사율)

Surface radiance

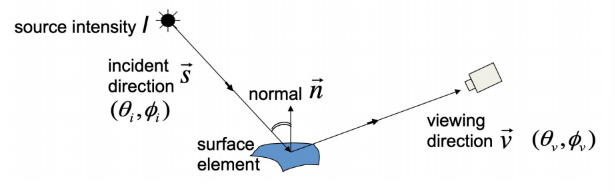
• Lambertian BRDF: $f(\theta_i,\varphi_i;\theta_r,\varphi_r) = \frac{\theta_v, \varphi_v}{E(\theta_i,\varphi_i)}=\frac{\rho_d}{\pi}$
• Radiance intensity: $I=\frac{d\Phi_i}{dw}$
• Surface irradiance: $E(\theta_i,\varphi_i) = \frac{d\Phi}{dA}$
• Surface radiance: $L(\theta_v, \varphi_v) = \text{BRDF}\times E = \frac{\rho_d}{\pi}\frac{d\Phi_i}{dA} = \frac{\rho_d}{\pi}\frac{d\Phi_i}{dw}\cos\theta_i = \frac{\rho_d}{\pi}I\cos\theta_i$
  $f=\frac{L}{E} \rightarrow L=fE$

식을 보면 알 수 있듯이 $\theta_i$가 커질수록 반사되는 양이 적어짐

Specular Reflection and Mirror BRDF

Mirror BRDF

• incident light는 하나의 방향으로만 반사됨 (only when $\vec v = \vec r$ )
  $\theta$가 같고 $\phi$가 opposite side에 있을 때에만 빛을 볼 수 있음
  
  이 사진에서 viewing direction은 specular direction과 다르므로 incident light를 볼 수 X
• double-delta function으로 표현 가능
  $f(\theta_i,\varphi_i;\theta_v,\varphi_v) = \rho_s \delta(\theta_i-\theta_v)\delta(\varphi_i+\pi-\varphi_v)$
  • $\rho_s$ : specular albedo
  • delta function은 변수가 0이 아니면 output이 0
• surface radiance: $L = I\rho_s\delta(\theta_i-\theta_v)\delta(\varphi_i + \pi - \varphi_v)$
  들어오는 빛이 그대로 바로 반사되기 때문에 BRDF 값 그대로가 L값이 됨

Combing Specular and Diffuse: Dichromatic Reflection

$\text{Observed Image Color} = a\times\text{Body Color} + b\times\text{Specular Color}$

body color와 specular color는 모두 벡터(RGB)
→ observed image color는 두 벡터의 합

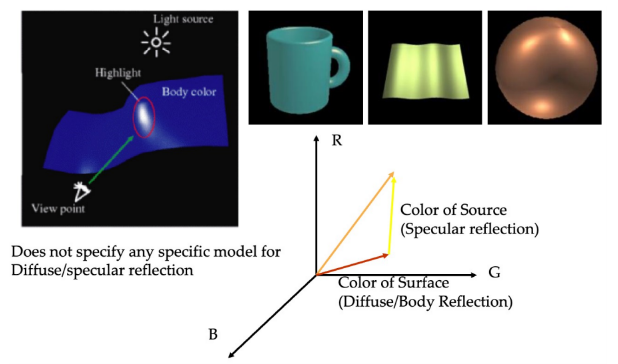
diffuse + specular에서 specular를 빼면 diffuse 구할 수 있음
→ natural color 구할 수 있음