그래프의 정점을 어떻게 벡터로 표현할까?
정점 표현 학습
정점 표현 학습이란
- 그래프의 정점들을 벡터의 형태로 표현하는 것
- 정점 표현 학습 = 정점 임베딩 (Node Embedding)
- 정점 임베딩은 벡터 형태의 표현 그 자체를 의미
- 정점이 표현되는 벡터 공간을 임베딩 공간이라 부름
- 각 정점 u 에 대한 임베딩, 즉 벡터 표현 가 정점 임베딩의 출력
왜 정점 임베딩을 사용할까
- 벡터 형태의 데이터를 여러 툴에 사용할 수 있기 때문
- 더이상 그래프 형태로 처리하지 않고 벡터로 처리함으로써 다양한 툴 사용 가능해짐
- 툴 : 분류기 (로지스틱 회귀분석) , 군집 분석 알고리즘, 정점 분류 등
정점 표현 학습의 목표
- 어떤 기준으로 정점을 벡터로 변환할까?
- 그래프에서의 정점간 유사도를 임베딩 공간에서도 보존!
- 임베딩 공간에서의 유사도는 내적을 사용
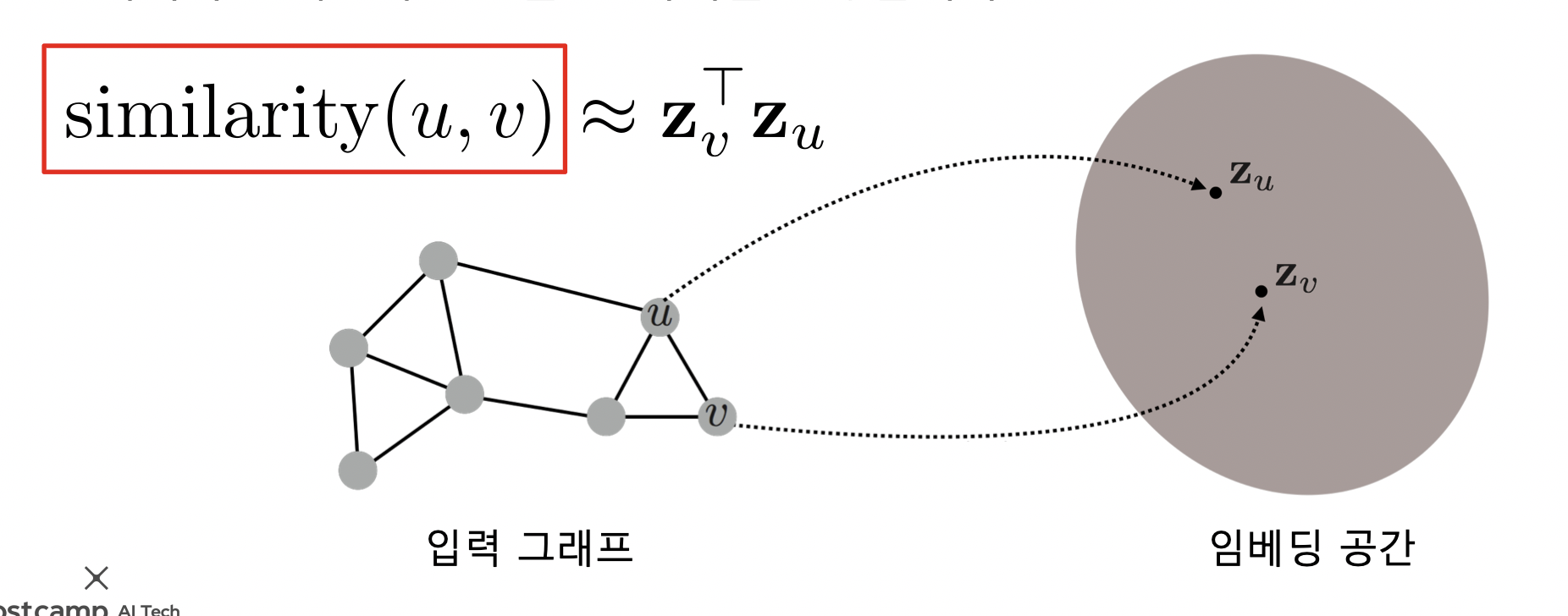
- 내적은 두 벡터가 클 수록, 같은 방향일수록 커짐
- 그래프의 두 정점 간 유사도는 여러가지 방법이 있음
- 인접성 기반 접근법
- 거리/경로/중첩 기반 접근법
- 임의보행 기반 접근법
- 정리
- 그래프에서 정점 유사도를 정의
- 정의한 유사도를 보존하도록 정점 임베딩 학습
인접성 기반 접근법
인접성 기반 접근법이란
- 그래프의 두 정점 간 유사도를 인접행렬로 나타냄
- 인접성 (Adjacency) 기반 접근법에서는 두 정점이 인접할 때 유사하다고 간주
- 두 정점 u 와 v 가 인접하다는 뜻은 둘을 직접 연결하는 간선 (u, v) 가 있음
- 인접행렬로 간선이 있으면 1, 없으면 0 으로 표현
- 인접성 기반 접근법의 손실함수가 최소화되는 정점 임베딩을 찾는 것이 목표
- 최소화 기법으로 SGD 등 사용
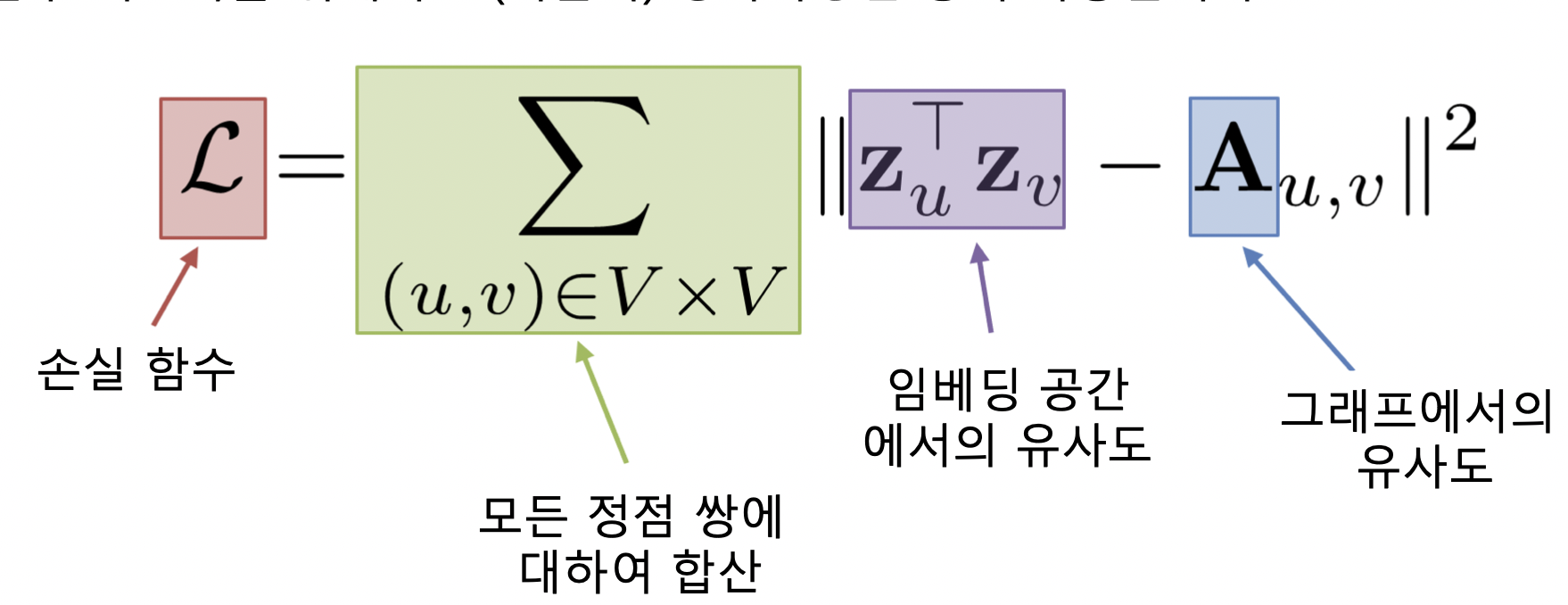
- 한계점
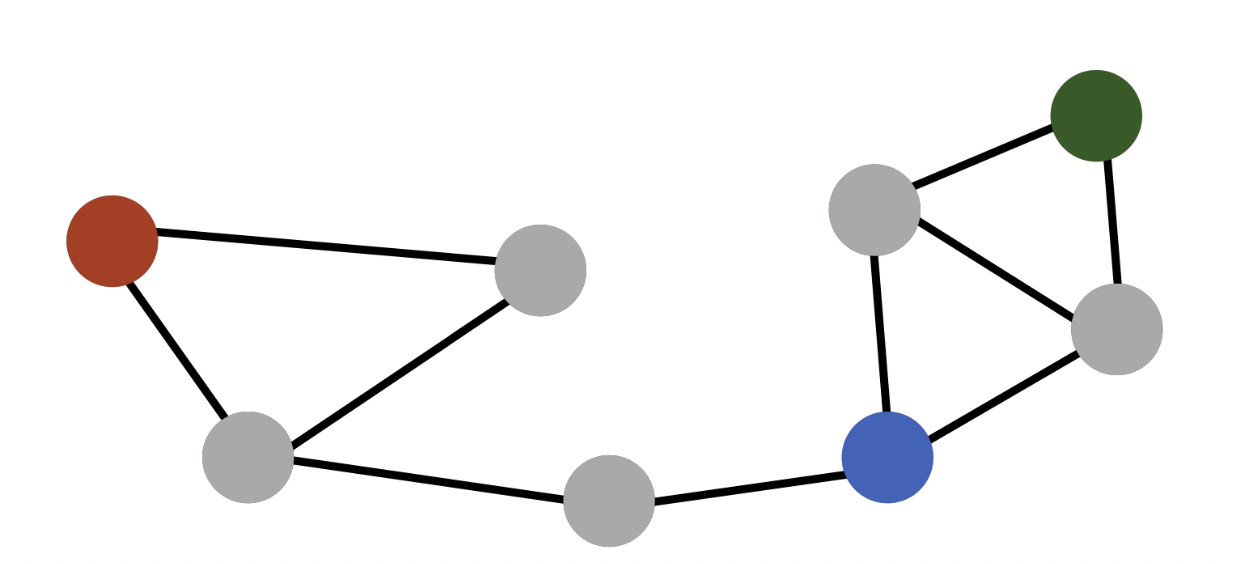 )
)
- 빨강-초록, 파랑-초록 인접성은 0 이지만 초록-파랑이 같은 군집에 속한다는 정보를 반영할 수 없음
거리/경로/중첩 기반 접근법
거리 기반 접근법
- 두 정점 사이의 거리가 충분히 가까운 경우 유사하다고 간주
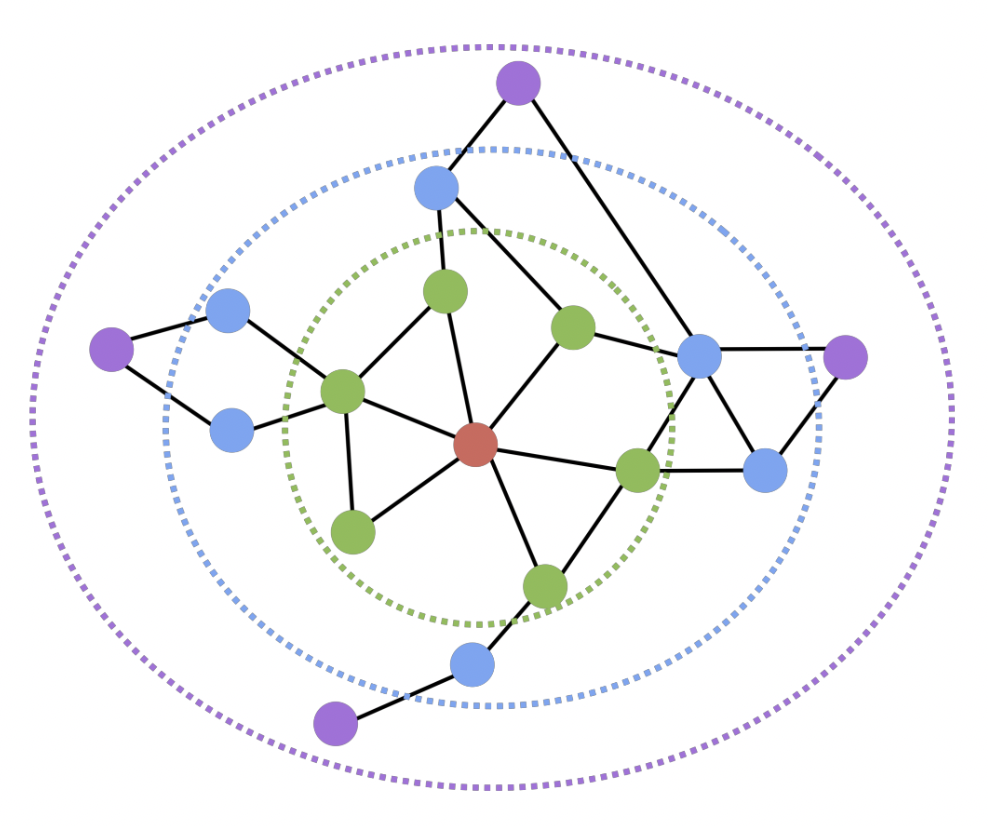
- 충분히의 기준을 거리 2 라고 가정해보자
- 빨강 기준, 초록과 파랑은 거리 2 안에 들어오므로 유사도 1 부여, 보라색은 유사도 0 부여
경로 기반 접근법
- 두 정점 사이의 경로가 많을 수록 유사하다고 간주
- 경로는 u 에서 시작해서 v 로 끝나고 순열에서 연속된 정점은 간선으로 연결됨을 만족하는 순열
- : 경로 중 거리가 k 인것의 수
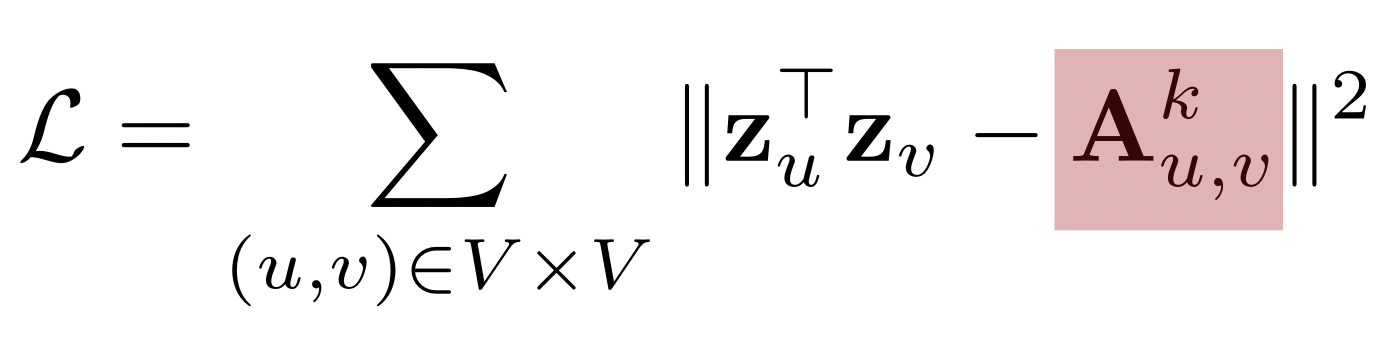
중첩 기반 접근법
- 두 정점이 많은 이웃을 공유할 수록 유사
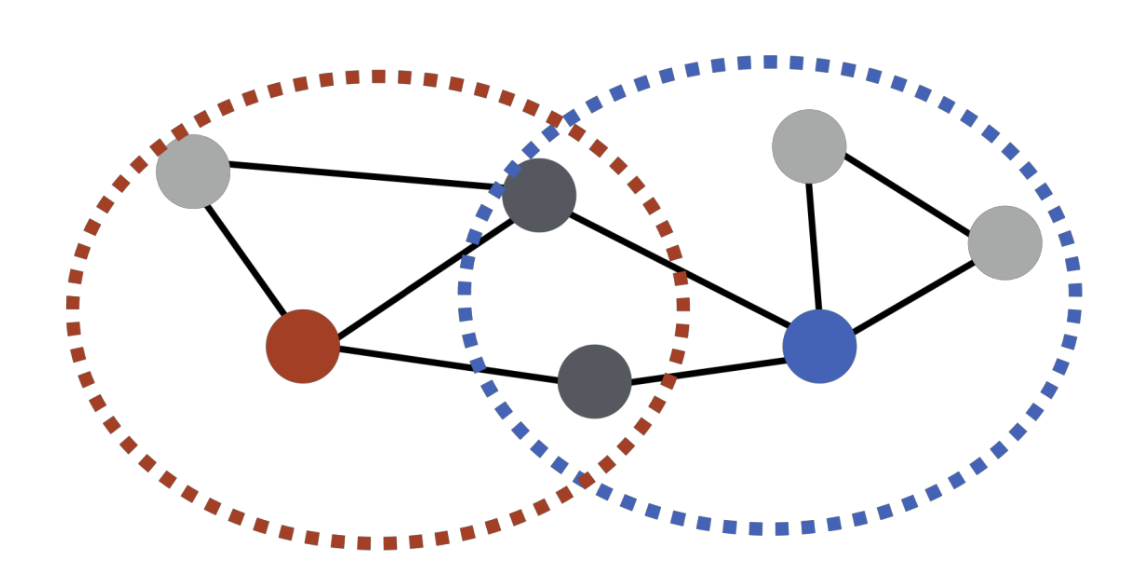
- 파랑과 빨강은 노드 2 개를 공유하므로 유사도 2

- 정점 u 의 이웃 집합 N(u)
- 공통 이웃 수 대신 자카드 유사도 or Adamic Adar 점수 사용 가능
- 자카드 유사도는 공통 이웃의 수 대신 비율을 계산
- N(u) 와 N(v) 의 교집합 / 이들의 합집합
- 0 ≤ 자카드 유사도 ≤ 1 (N(u) 와 N(v) 가 같으면 1)
- Adamic Adar 는 공통 이웃 각각에 가중치를 부여하여 가중합 계산
- 자카드 유사도는 공통 이웃의 수 대신 비율을 계산
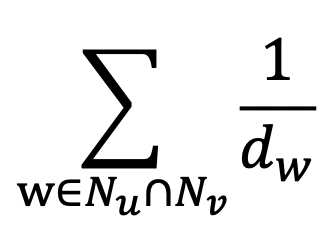
임의보행 기반 접근법
임의보행 기반 접근법이랑
- 한 정점에서 시작하여 임의보행을 할 때 다른 정점에 도달할 확률을 유사도로 간주
- 임의보행은 현재 정점의 이웃 중 하나를 균일한 확률로 이동하는 반복 과정
- 임의보행은 시작 정점 주변의 지역적 정보와 그래프 전역 정보를 모두 고려한다는 장점이 있음
- 그래프 전역 정보 사용? 기존 방법들은 거리를 k 로 제한했지만 임의보행은 거리 제한 없음
- 과정
- 각 정점에서 시작하여 임의보행 반복 수행
- 각 정점에서 임의보행하여 도달한 정점들의 리스트 기록함. 정점 u 로부터 임의보행 중 도달한 정점들의 리스트는 라고 함. 한 정점을 여러 번 도달하면 해당 정점은 여러 번 포함됨
- 아래 로스 함수를 최소화하는 임베딩을 학습

- 어떻게 임베딩으로부터 도달 확률을 추정할까?
- P(v | ) 를 아래와 같이 추정
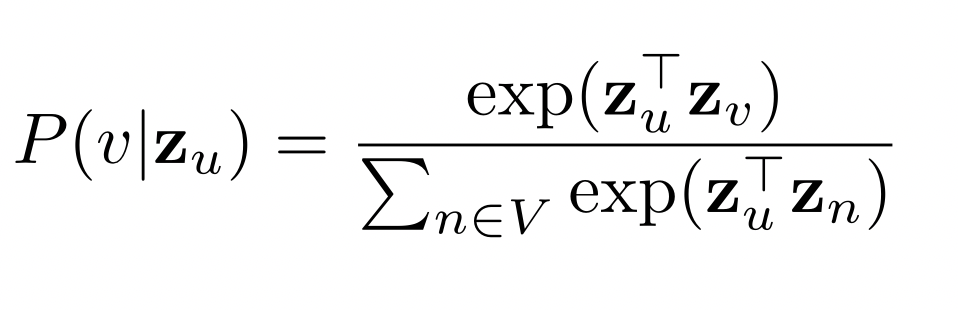
- 유사도 (내적) 이 높을 수록 도달 확률이 높음
- 추정한 도달 확률로 손실함수 재정의, 손실함수를 최소화하는 임베딩 학습

DeepWalk 와 Node2Vec
- 딥워크
- 앞서 설명한 기본적인 임의 보행
- 현재 정점의 이웃 중 하나를 균일한 확률로 반복 이동
- Node2Vec
- 2차 치우친 임의 보행 (Second-order Biased Random Walk) 사용
- 현재 정점 + 직전 정점 고려하여 다음 정점 선택
- 직전 정점의 거리를 기준으로 구분하여 차등적인 확률 부여, 부여하는 확률에 따라 다른 종류의 임베딩을 얻음
- 2차 치우친 임의 보행 (Second-order Biased Random Walk) 사용
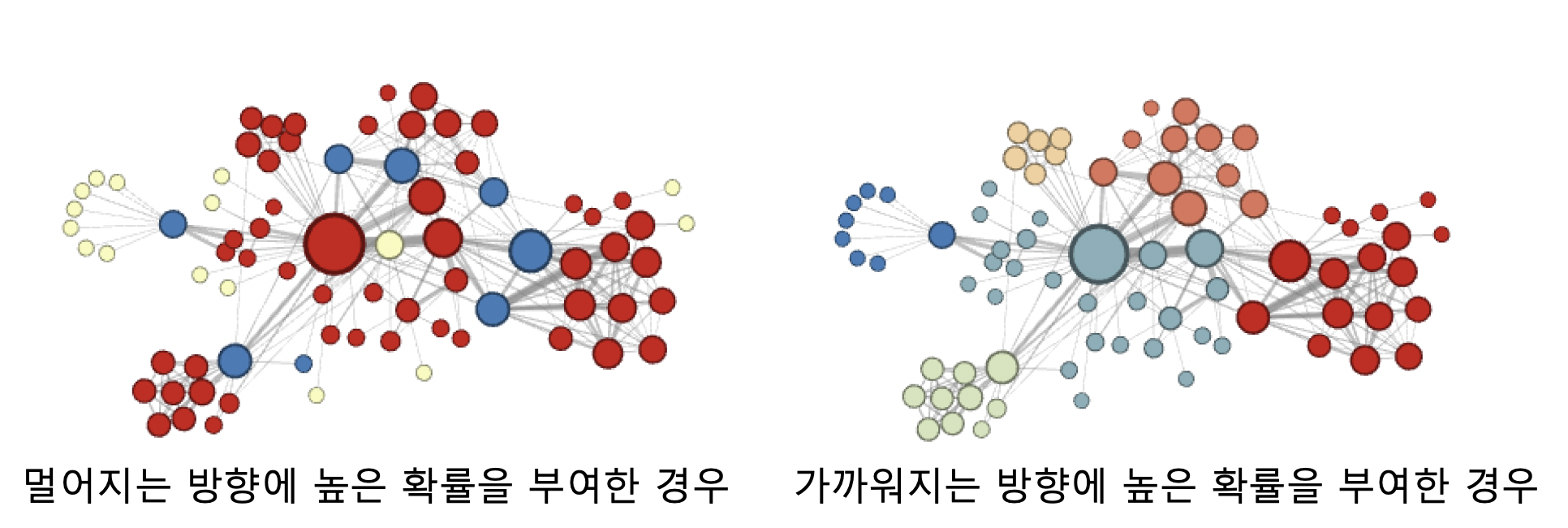
- 멀어지는 방향에 높은 확률 부여한 경우, 정점의 **역할** (다리 역할, 변두리 정점 등) 이 같은 경우 임베딩 유사
- 가까워지는 방향에 높은 확률 부여한 경우, 같은 **군집**에 속한 경우 임베딩 유사손실 함수 근사
- 임의보행 기법의 손실함수는 계산 시간은 정점의 수 제곱 비례 (중첩된 합 때문)
- 정점이 많을 경우 시간 매우 오래 걸림
- 이를 막기 위해 근사식 사용, 모든 정점에 대해 정규화하는 대신 몇 개의 정점을 뽑아서 비교, 뽑힌 정점들을 네거티브 샘플이라 부름

- 연결성에 비례하는 확률로 네거티브 샘플로 뽑힐 확률 높아짐, 네거티브 샘플이 많을 수록 학습이 안정적
변환식 정점 표현 학습의 한계
변환식 정점 표현 방법과 귀납식 정점 표현 방법
- 변환식 정점 표현 방법
- 지금까지 본 정점 임베딩 방법들은 변환식 (Transductive) 방법
- 변환식 방법은 학습의 결과로 정점의 임베딩 자체를 얻는다는 특성이 있음
- 귀납식 정점 표현 방법
- 정점을 임베딩으로 변화시키는 함수, 인코더를 얻음
- 변환식 임베딩 방법의 한계
- 학습이 진행된 이후에 추가된 정점에 대해서는 임베딩 불가능
- 모든 정점에 대한 임베딩 미리 계산해야함
- 정점의 속성 정보 활용 못 함
- 이러한 한계를 극복하기 위해 귀납식 임베딩 방법인 그래프 신경망 (GNN) 사용
군집 분석
- Girvan-Newman or Louvain 같이 군집을 찾아나서거나
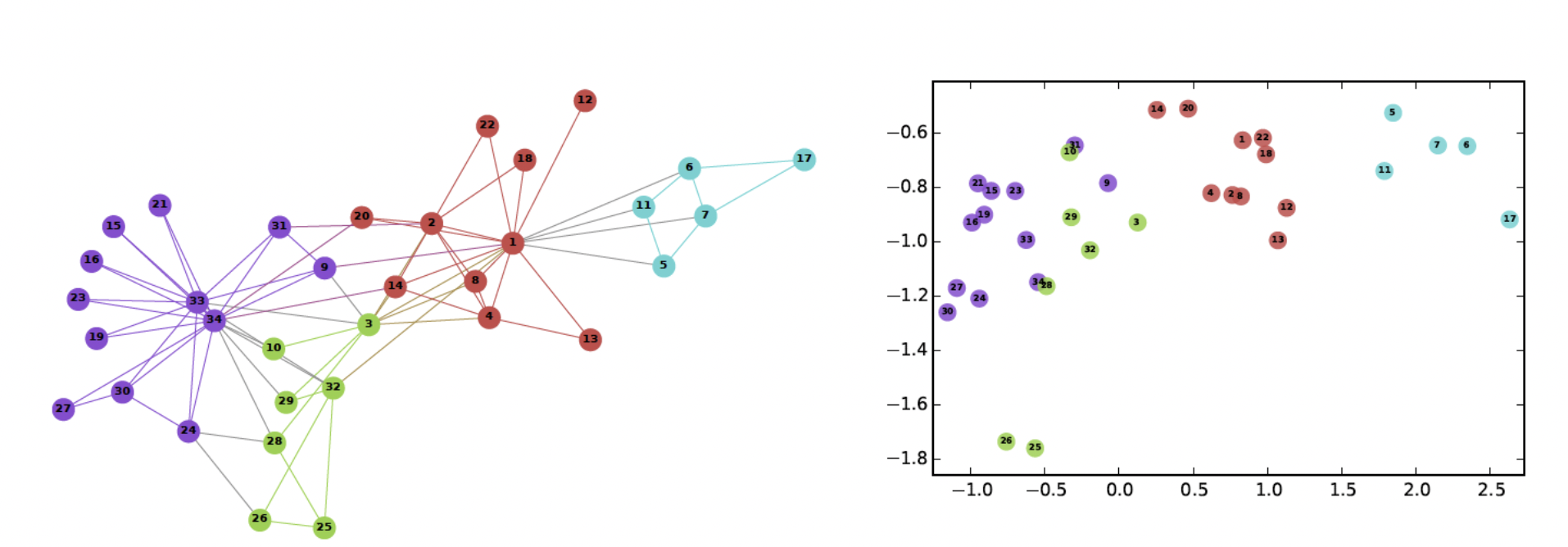
- Node2Vec 으로 유사한 노드들을 임베딩해주고 K-Means 로 클러스터링해주거나
Further Reading
https://arxiv.org/pdf/1607.00653.pdf
https://arxiv.org/pdf/1403.6652.pdf
참조
BoostCamp AI Tech
