그래프의 구조를 어떻게 분석할까?

군집

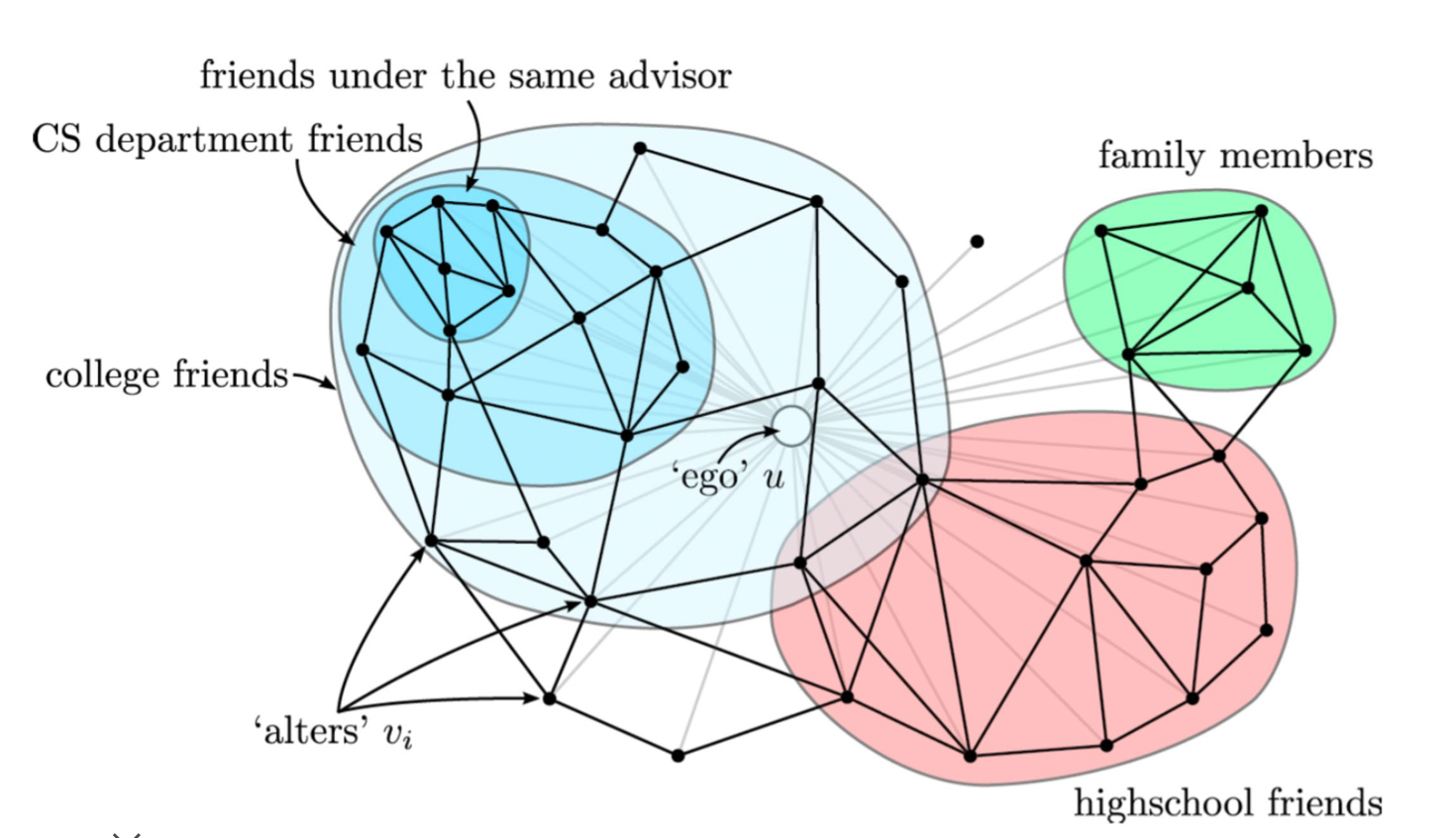
• 온라인 소셜 네트워크의 군집들은 사회적 무리 (Social Circle) 을 의미하는 경우가 많음
• 소셜 네트워크의 군집들이 부정 행위와 관련된 경우도 있음
• 조직 내 분란이 소셜 네트워크 상의 군집으로 표현된 경우도 있음
• 뉴런간 연결 그래프에서는 군집들이 뇌의 특정 기능을 담당
  -> 이렇듯 군집은 정점 간의 특별한 관계를 알려주기도 함

군집 탐색 문제

• 그래프를 여러 군집으로 잘 나누는 문제를 군집 탐색 (Community Detection) 문제라 함
• 보통은 각 정점이 한 개의 군집에 속하도록 나눔
• 비지도 기계학습 문제인 클러스터링과 유사

군집 구조의 통계적 유의성과 군집성

비교 대상 : 배치 모형


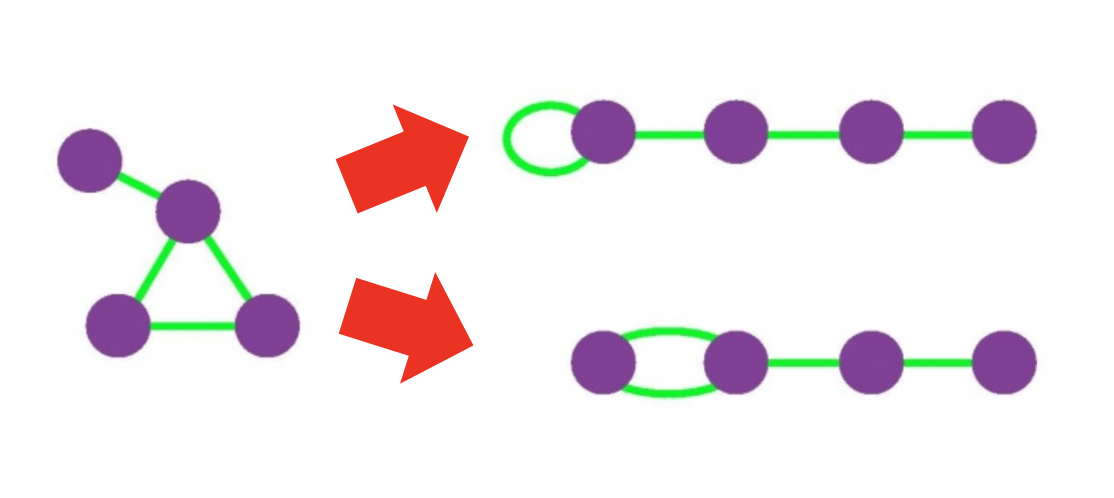
• 성공적인 군집 탐색을 정의하기 위해 배치 모형 사용
• 주어진 그래프에 대한 배치 모형은 각 정점의 연결성을 보존한 상태에서 간선들을 무작위로 재배치하여 얻은 그래프를 의미함
• 배치 모형에서 임의의 두 정점 i 와 j 사이에 간선이 존재할 확률은 두 정점의 연결성에 비례

군집성

• 군집 탐색의 성공 여부를 판단하기 위해 군집성 사용
• 그래프와 군집들의 집합 S 가 주어졌을 때 각 군집 s 가 군집의 성질을 잘 만족하는지 살펴보기 위해, 군집 내부의 간선의 수를 그래프와 배치 모형에서 비교

• 기댓값 사용하는 이유 : 배치 모형이 무작위성을 포함하기 때문

• -1 ≤ 군집성 ≤ 1

• 배치 모형과 비교해서 그래프에서 군집 내부 간선의 수가 많을 수록, 위 식의 값이 커질 수록 성공한 군집 탐색

• 군집성은 무작위로 연결된 배치 모형과의 비교를 통해 통계적 유의성을 판단

• 항상 -1 과 1 사이의 값을 가짐

• 0.3~0.7 정도 값을 가질 때 그래프에 존재하는 통계적으로 유의미한 군집들을 찾아냈다고 볼 수 있음

• 예시
  

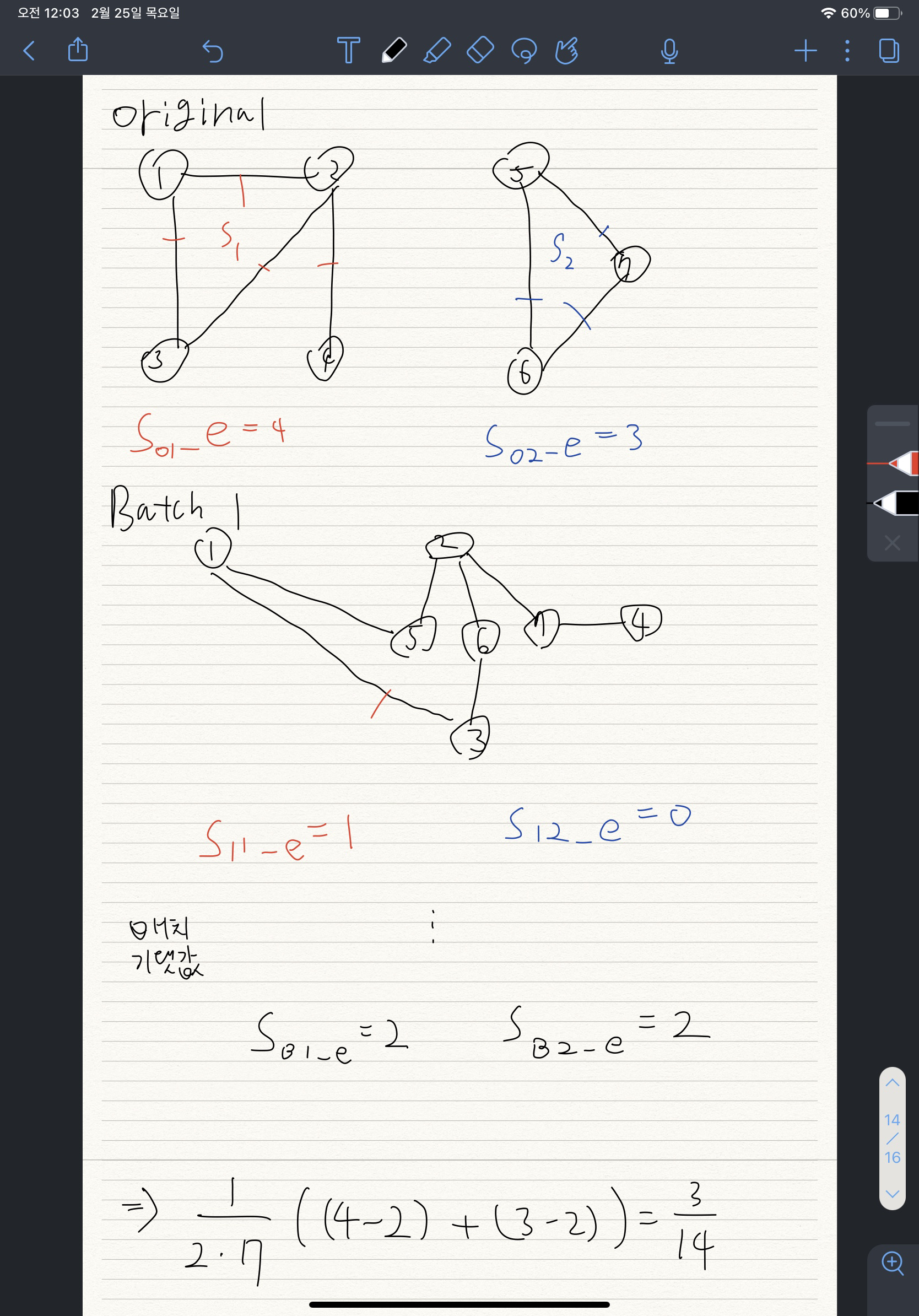
  • 배치 모형은 전체 그래프에 대해 만들고 해당 군집 노드끼리 연결되는 엣지만 체크함

군집 탐색 알고리즘

Girvan-Newman 알고리즘

• 하향식, 탑-다운 군집 탐색 알고리즘
• 전체 그래프에서 탐색을 시작해서 군집들이 서로 분리되도록 간선을 순차적으로 제거
• 서로 다른 군집을 연결하는 다리 역할의 간선을 제거
• 다리 역할의 간선을 어떻게 찾을 수 있을까?
  • 간선의 매개 중심성 (Betweenness Centrality) 사용
  • 해당 간선이 정점 간의 최단 경로에 놓이는 횟수

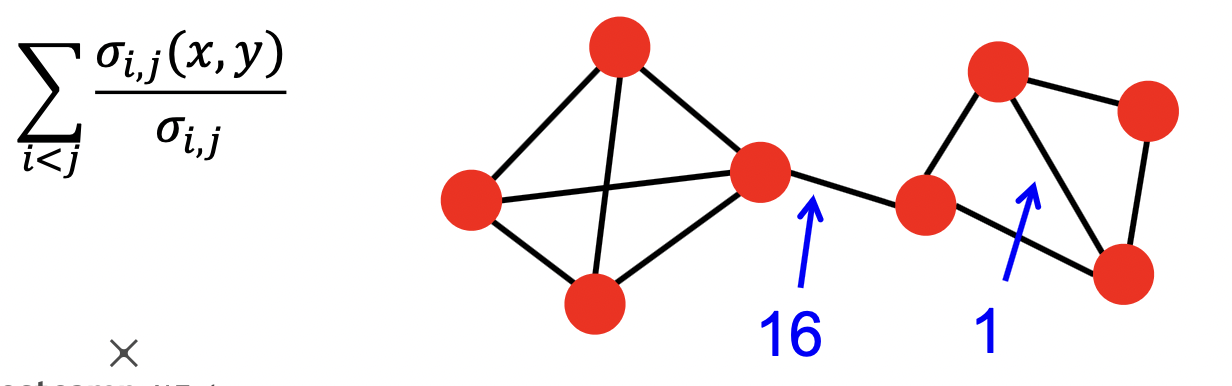
• 매개 중심성이 높은 간선을 순차적으로 제거
  • 단계마다 새로 매개 중심성 파악
• 모든 간선이 제거될 때까지 수행
• iteration 에 따라 다른 입도 (Granularity) 의 군집 구조가 나타남
• 간선을 어느 정도 제거하는 것이 가장 적합할까?
  • 군집성이 최대가 되는 지점까지 간선 제거
  • 단, 현재의 연결 요소들을 군집으로 가정하되, 입력 그래프에서 군집성 계산

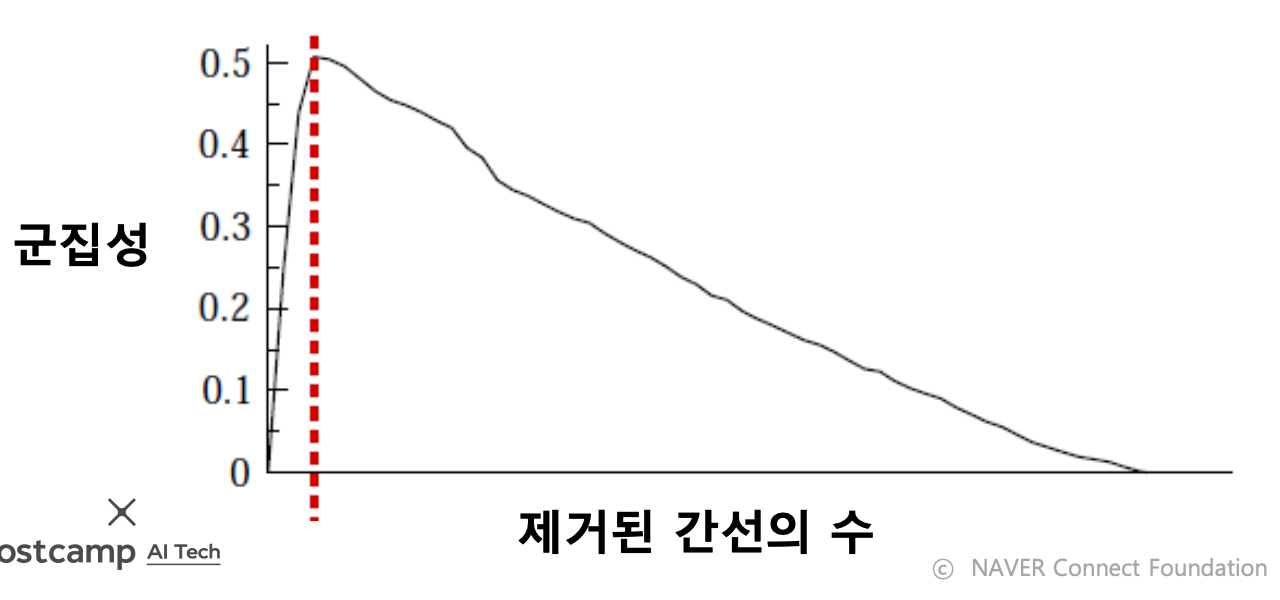
• 과정 정리
  • 전체 그래프에서 시작
  • 매개 중심성이 높은 순서로 간선 제거하면서 군집성의 변화를 기록
  • 군집성이 가장 커지는 상황 복원
  • 이 때 서로 연결된 정점들, 연결 요소를 하나의 군집으로 간주

Louvain 알고리즘

• 상향식, 바텀-업 군집 탐색 알고리즘
• 개별 정점에서 시작해서 점점 큰 군집 형성
• 어떤 기준으로 군집을 합칠까?
  • 군집성
• 과정 정리
  • 1) 개별 정점으로 구성된, 크기 1의 군집들로부터 시작
  • 2) 각 정점 u 를 기존 혹은 새로운 군집으로 이동함. 이 때, 군집성이 최대화되도록 군집을 결정
  • 3) 더이상 군집성이 증가하지 않을 때까지 2) 반복
  • 4) 각 군집을 하나의 정점으로하는 군집 레벨의 그래프를 얻은 뒤 3) 을 수행
  • 5) 한 개의 정점이 남을 때까지 4) 반복

중첩이 있는 군집 탐색

• 실제 그래프의 군집들은 중첩되어 있는 경우가 많음
  • 소셜 네트워크에서 개인은 여러 사회적 역할을 수행
  • 위의 두 알고리즘은 한 정점은 한 군집이라 가정했음

• 중첩 군집 모형
  • 각 정점은 여러 개의 군집에 속할 수 있음
  • 각 군집 A 에 대하여 같은 군집에 속하는 두 정점은 $P_A$ 확률로 간선 연결
  • 두 정점이 여러 군집에 동시에 속할 경우 간선 연결 확률은 독립적
    • A 와 B 에 동시에 속할 경우 두 정점이 간선으로 직접 연결될 확률은 1-(1-PA)(1-PB)
  • 어느 군집에도 함께 속하지 않는 두 정점은 낮은 확률 e 로 직접 연결됨
• 중첩 군집 모형이 주어지면, 주어진 그래프의 확률을 계산할 수 있음
  • 그래프의 확률은 다음 확률들의 곱
    • 그래프의 각 간선의 두 정점이 (모형에 의해) 직접 연결될 확률
    • 그래프에서 직접 연결되지 않은 각 정점 쌍이 (모형에 의해) 직접 연결되지 않을 확률

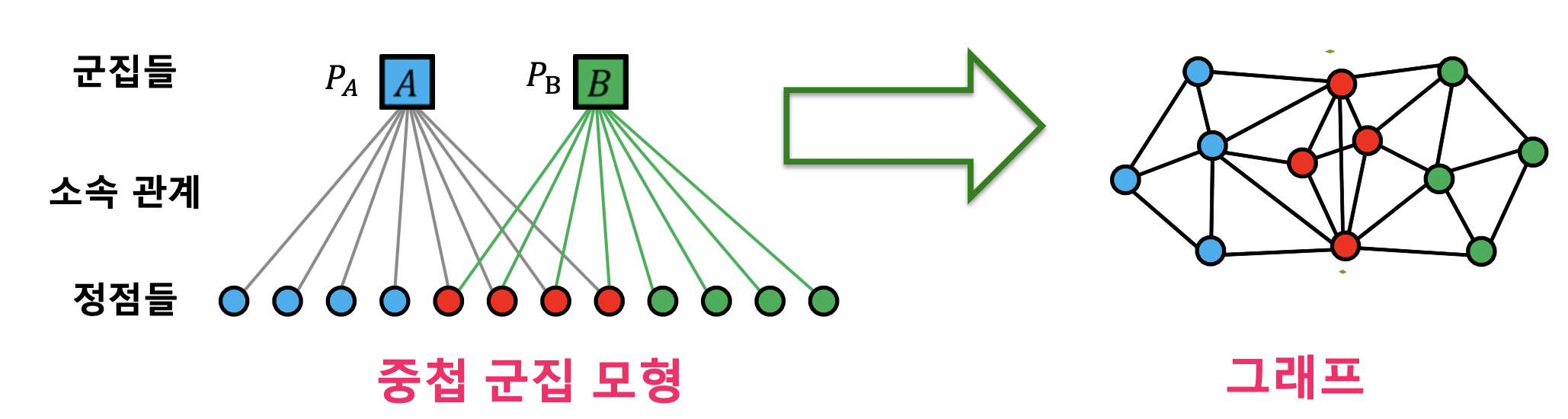
• 중첩 군집 탐색은 주어진 그래프의 확률을 최대화하는 중첩 군집 모형을 찾는 과정
  • 최우도 추정치 (MLE) 를 찾는 과정

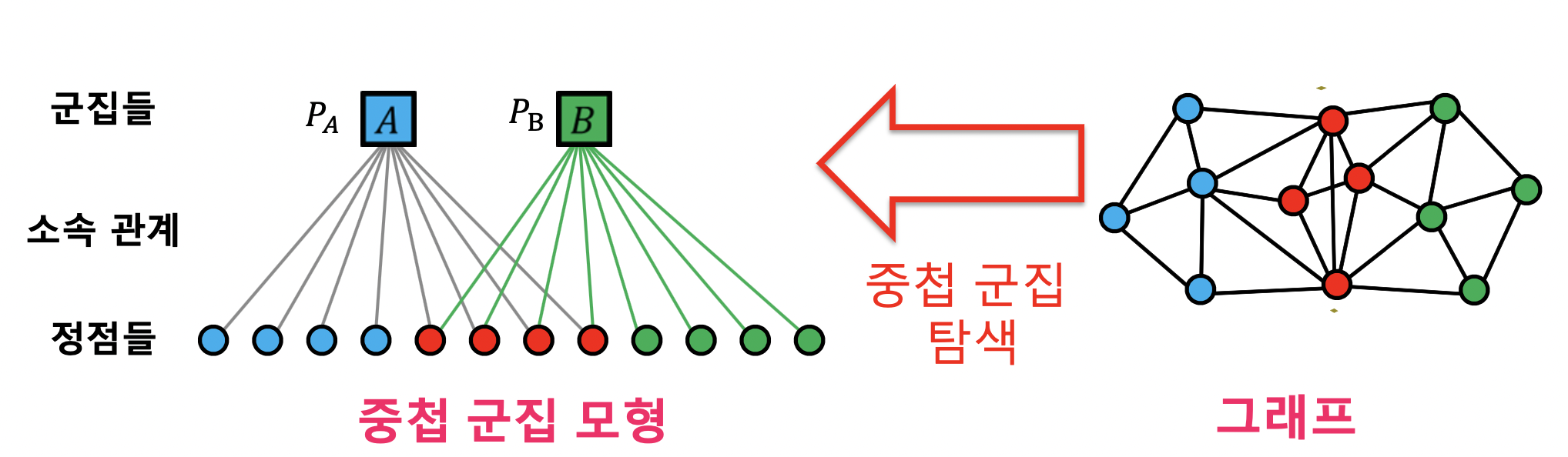
• 각 정점이 각 군집에 속한다, 속하지 않는다 (1, 0) 이산적으로 나오기 때문에 최적화 방법 (경사하강법 등) 을 사용할 수 없어서 중첩 군집 탐색 힘듦

완화된 중첩 군집 모형

• 완화된 중첩 군집 모형을 통해 중첩 군집 탐색 용이해짐
• 각 정점이 각 군집에 속해 있는 정도를 실숫값으로 표현, 중간 상태 표현 가능

• 모형의 매개변수들이 실숫값을 가지므로 최적화 도구 (경사하강법 등) 을 사용하여 모형을 탐색할 수 있음

Further Reading

• http://infolab.stanford.edu/~ullman/mmds/ch10n.pdf

---

참조

• BoostCamp AI Tech