개요
제약조건 하에 원하는 성능을 최대로 하면서 비용은 최소화하는 optimization 에 대해 배운다.
Problem, Computation, Decision, and Optimization
Problem
문제는 바라는 것과 인식하는 것의 차이이다.
문제를 해결하기 위해서는 제약조건 아래에서 결정 (계산) 을 반복하며 원하는 결과를 도출할 수 있다.
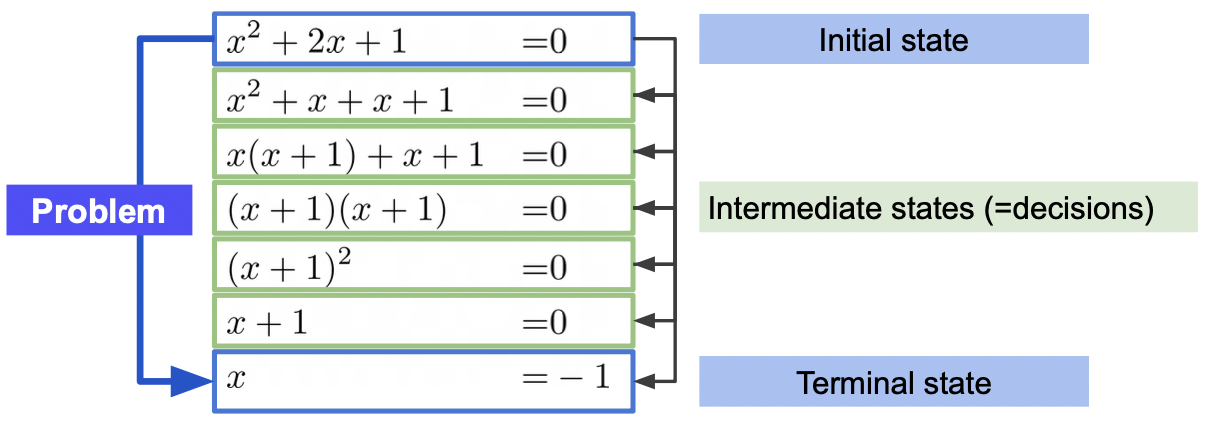
Computation
정해진 방법대로 유한 혹은 무한 회 계산하는 행위를 말한다.
문제 해결에서 결정을 위해 정해진 방법으로 계산을 수행한다.
Decision
Inference
문제 해결을 위해 한 스텝씩 결정을 한다.
딥러닝에서는 주어진 모델 M 과 실수 k 가 주어졌을 때, M 이 최대 k 를 만족하는 validation loss 를 구하는 문제가 해당된다.
Optimization
Inference with min val-loss
주어진 모델 M 이 가장 최저의 validation loss 를 만족시키는 parameter 집합을 구하는 문제가 해당된다.
Decision 을 반복적으로 computation 하면서 최저 loss 를 찾는 과정이 optimization 이다.
구체적으로는 Adam, SGD 등의 optimizer 를 통해 다음 스텝의 파라미터를 수정해나간다.
Constraints
서울에서 부산을 가는 길을 찾을 때, 시간이나 금전적인 제한이 없다면 무한한 답이 도출될 수 있다.
따라서 이 문제에서는 시간이나 돈에서 제한 사항을 두면 가장 적절한 길을 찾을 수 있게 된다.
Objective 에 따라 Constraints 가 달라진다.
결정 문제에서는 주어진 constraint 에서 최고의 성능 (결정) 을 해야 한다.
최적화 문제에서는 N 번의 step 동안 얻은 cost 의 합이 constraint 를 넘지 않아야 한다.
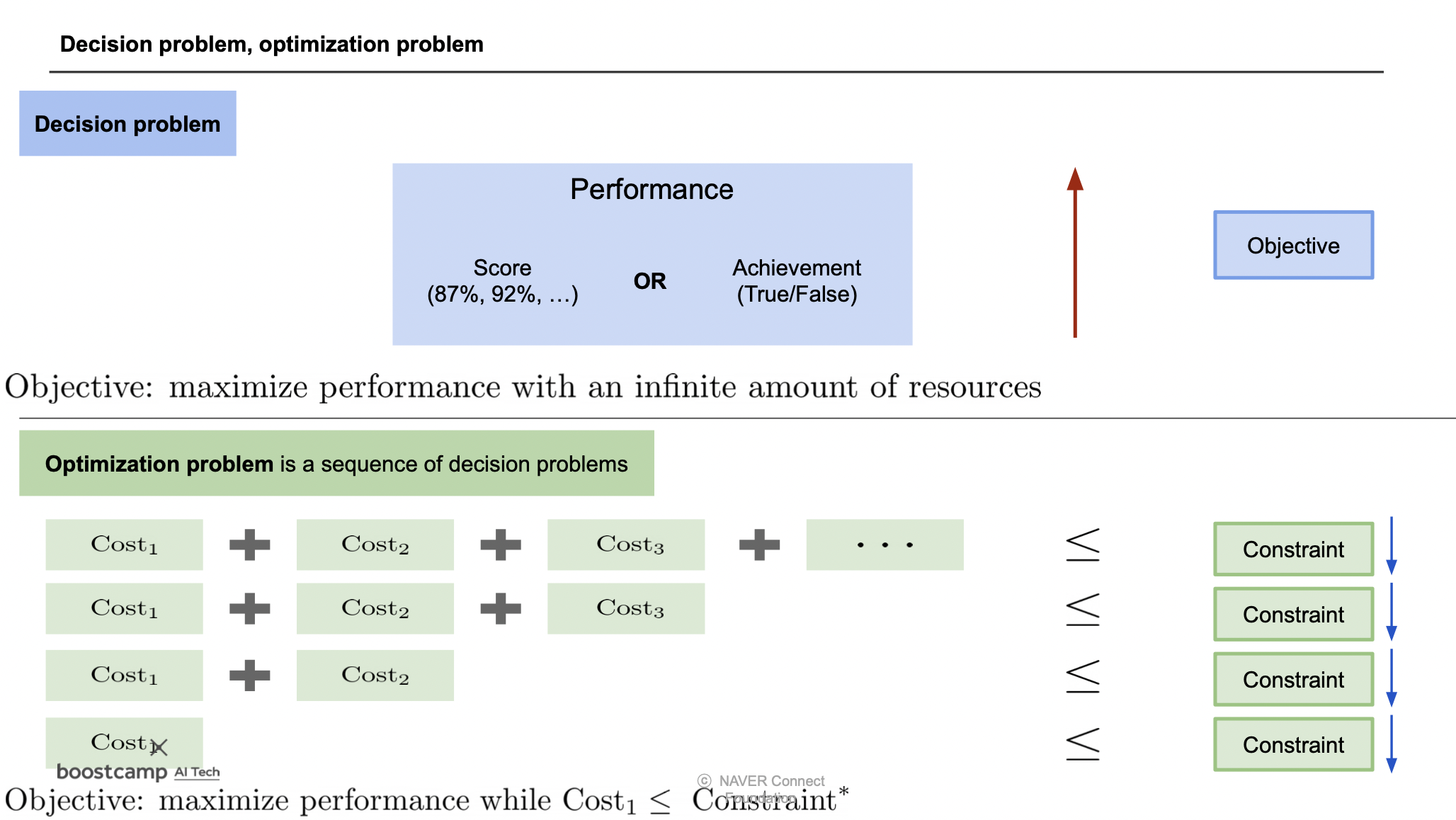
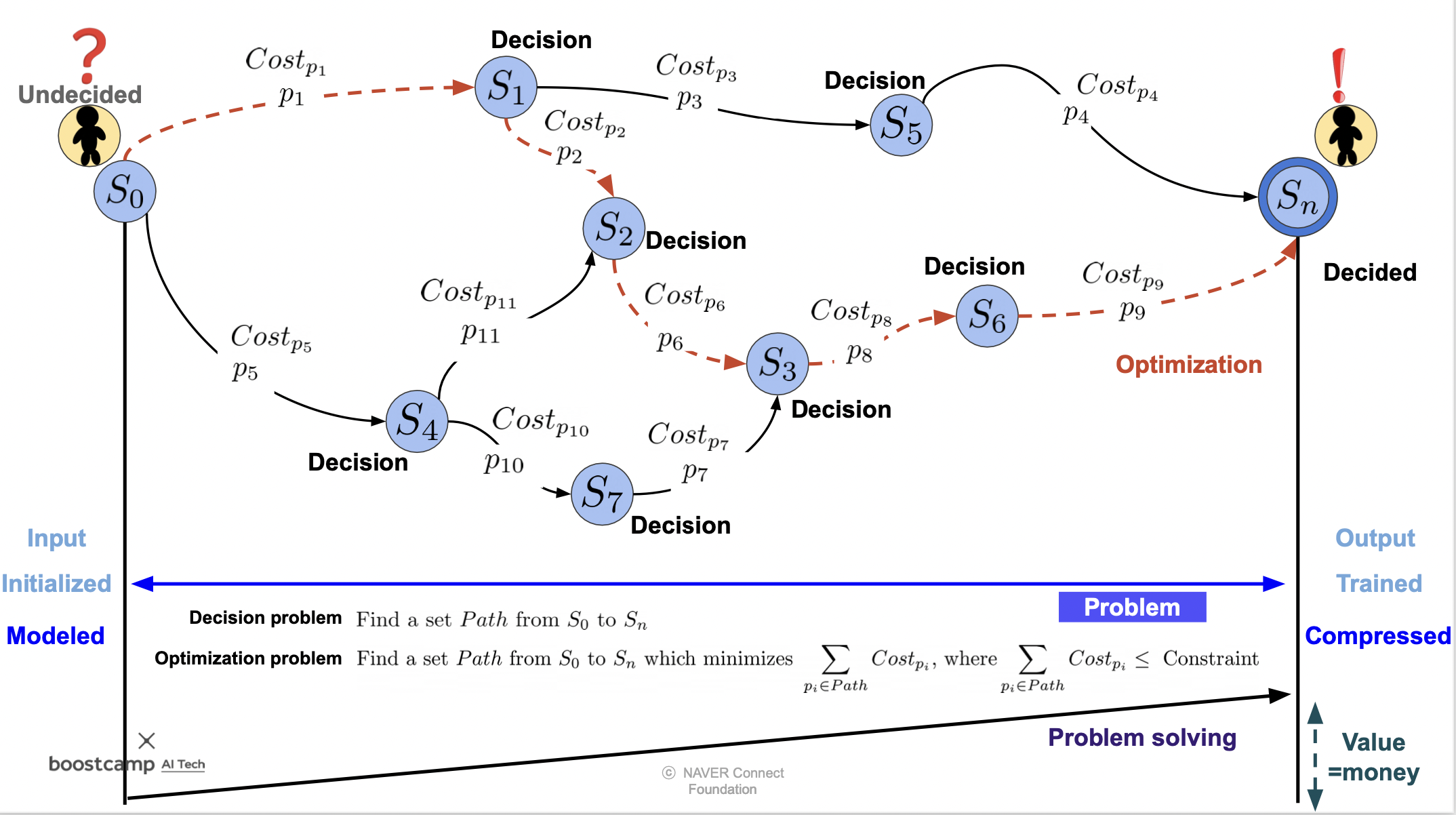
Constraints in Model Compression
모델 압축 (경량화) 문제에서는 모델을 작은 모델로 만들기 위해 최적화를 수행한다.
이 때, 성능에 집중할지, 용량에 집중할지 등의 constraint 를 고려해야 한다.
참조
BoostCamp AI Tech
